"This is the relativity problem: to fix objectively a class of
equivalent coordinatizations and to ascertain the group of
transformations S mediating between them."
— Hermann Weyl, The Classical Groups,
Princeton University Press, 1946, p. 16
|
From some 1949 remarks of Weyl— "The relativity problem is one of central significance throughout geometry and algebra and has been recognized as such by the mathematicians at an early time." — Hermann Weyl, "Relativity Theory as a Stimulus in Mathematical Research," Proceedings of the American Philosophical Society , Vol. 93, No. 7, Theory of Relativity in Contemporary Science: Papers Read at the Celebration of the Seventieth Birthday of Professor Albert Einstein in Princeton, March 19, 1949 (Dec. 30, 1949), pp. 535-541 Weyl in 1946—: "This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them." — Hermann Weyl, The Classical Groups , Princeton University Press, 1946, p. 16 |
For some context, see Relativity Problem in this journal.
In the case of PG(3,2), there is a choice of geometric models
to be coordinatized: two such models are the traditional
tetrahedral model long promoted by Burkard Polster, and
the square model of Steven H. Cullinane.
The above Wikipedia section tacitly (and unfairly) assumes that
the model being coordinatized is the tetrahedral model. For
coordinatization of the square model, see (for instance) the webpage
Finite Relativity.
For comparison of the two models, see a figure posted here on
May 21, 2014 —
Labeling the Tetrahedral Model (Click to enlarge) —
"Citation needed" —
The anonymous characters who often update the PG(3,2) Wikipedia article
probably would not consider my post of 2014, titled "The Tetrahedral
Model of PG(3,2)," a "reliable source."
“This is the relativity problem: to fix objectively a class of
equivalent coordinatizations and to ascertain the group of
transformations S mediating between them.”
— Hermann Weyl, The Classical Groups ,
Princeton University Press, 1946, p. 16
See also Relativity Problem and Diamonds and Whirls.
A sequel to last night's post The 4×4 Relativity Problem —
In other words, how should the triangle corresponding to
the above square be coordinatized ?
See also a post of July 8, 2012 — "Not Quite Obvious."
Context — "Triangles Are Square," a webpage stemming
from an American Mathematical Monthly item published
in 1984.
The sixteen-dot square array in yesterday’s noon post suggests
the following remarks.
“This is the relativity problem: to fix objectively a class of
equivalent coordinatizations and to ascertain the group of
transformations S mediating between them.”
— Hermann Weyl, The Classical Groups ,
Princeton University Press, 1946, p. 16
The Galois tesseract appeared in an early form in the journal
Computer Graphics and Art , Vol. 2, No. 1, February 1977—
The 1977 matrix Q is echoed in the following from 2002—
A different representation of Cullinane’s 1977 square model of the
16-point affine geometry over the two-element Galois field GF(2)
is supplied by Conway and Sloane in Sphere Packings, Lattices and Groups
(first published in 1988) :
Here a, b, c, d are basis vectors in the vector 4-space over GF(2).
(For a 1979 version of this vector space, see AMS Abstract 79T-A37.)
See also a 2011 publication of the Mathematical Association of America —
In the Beginning…
"As is well known, the Aleph is the first letter of the Hebrew alphabet."
– Borges, "The Aleph" (1945)
From some 1949 remarks of Weyl—
"The relativity problem is one of central significance throughout geometry and algebra and has been recognized as such by the mathematicians at an early time."
— Hermann Weyl, "Relativity Theory as a Stimulus in Mathematical Research," Proceedings of the American Philosophical Society , Vol. 93, No. 7, Theory of Relativity in Contemporary Science: Papers Read at the Celebration of the Seventieth Birthday of Professor Albert Einstein in Princeton, March 19, 1949 (Dec. 30, 1949), pp. 535-541
Weyl in 1946—:
"This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them."
— Hermann Weyl, The Classical Groups , Princeton University Press, 1946, p. 16
Coxeter in 1950 described the elements of the Galois field GF(9) as powers of a primitive root and as ordered pairs of the field of residue-classes modulo 3—
"… the successive powers of the primitive root λ or 10 are
λ = 10, λ2 = 21, λ3 = 22, λ4 = 02,
λ5 = 20, λ6 = 12, λ7 = 11, λ8 = 01.
These are the proper coordinate symbols….
(See Fig. 10, where the points are represented in the Euclidean plane as if the coordinate residue 2 were the ordinary number -1. This representation naturally obscures the collinearity of such points as λ4, λ5, λ7.)"
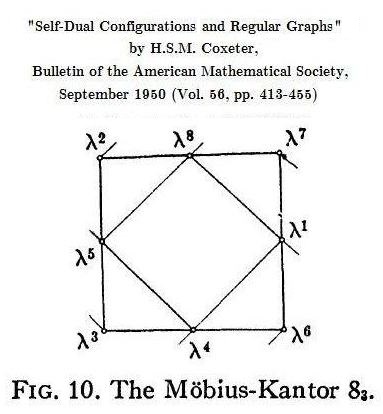
Coxeter's Figure 10 yields...
The Aleph
The details:
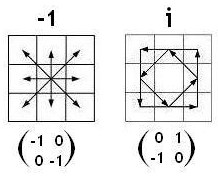
Coxeter's phrase "in the Euclidean plane" obscures the noncontinuous nature of the transformations that are automorphisms of the above linear 2-space over GF(3).
A footnote was added to Finite Relativity—
Background:
Weyl on what he calls the relativity problem—
“The relativity problem is one of central significance throughout geometry and algebra and has been recognized as such by the mathematicians at an early time.”
– Hermann Weyl, 1949, “Relativity Theory as a Stimulus in Mathematical Research“
“This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them.”
– Hermann Weyl, 1946, The Classical Groups , Princeton University Press, p. 16
…. A note of Feb. 20, 1986, supplied an example of such coordinatizations in finite geometry. In that note, the group of mediating transformations acted directly on coordinates within a 4×4 array. When the 4×4 array is embedded in a 4×6 array, a larger and more interesting group, M 24 (containing the original group), acts on the larger array. There is no obvious solution to Weyl’s relativity problem for M 24. That is, there is no obvious way* to apply exactly 24 distinct transformable coordinate-sets (or symbol-strings ) to the 24 array elements in such a way that the natural group of mediating transformations of the 24 symbol-strings is M 24. ….
Footnote of Sept. 20, 2011:
* R.T. Curtis has, it seems, a non-obvious way that involves strings of seven symbols. His abstract for a 1990 paper says that in his construction “The generators of M 24 are defined… as permutations of twenty-four 7-cycles in the action of PSL2(7) on seven letters….”
See “Geometric Interpretations of the ‘Natural’ Generators of the Mathieu groups,” by R.T. Curtis, Mathematical Proceedings of the Cambridge Philosophical Society (1990), Vol. 107, Issue 01, pp. 19-26. (Rec. Jan. 3, 1989, revised Feb. 3, 1989.) This paper was published online on Oct. 24, 2008.
Some related articles by Curtis:
R.T. Curtis, “Natural Constructions of the Mathieu groups,” Math. Proc. Cambridge Philos. Soc. (1989), Vol. 106, pp. 423-429
R.T. Curtis. “Symmetric Presentations I: Introduction, with Particular Reference to the Mathieu groups M 12 and M 24” In Proceedings of 1990 LMS Durham Conference ‘Groups, Combinatorics and Geometry’ (eds. M. W. Liebeck and J. Saxl), London Math. Soc. Lecture Note Series 165, Cambridge University Press, 1992, pp. 380–396
R.T. Curtis, “A Survey of Symmetric Generation of Sporadic Simple Groups,” in The Atlas of Finite Groups: Ten Years On , (eds. R.T. Curtis and R.A. Wilson), London Math. Soc. Lecture Note Series 249, Cambridge University Press, 1998, pp. 39–57
Weyl on what he calls the relativity problem—
"The relativity problem is one of central significance throughout geometry and algebra and has been recognized as such by the mathematicians at an early time."
— Hermann Weyl, 1949, "Relativity Theory as a Stimulus in Mathematical Research"
"This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them."
— Hermann Weyl, 1946, The Classical Groups, Princeton University Press, p. 16
Twenty-four years ago a note of Feb. 20, 1986, supplied an example of such coordinatizations in finite geometry. In that note, the group of mediating transformations acted directly on coordinates within a 4×4 array. When the 4×4 array is embedded in a 4×6 array, a larger and more interesting group, M24 (containing the original group), acts on the larger array. There is no obvious solution to Weyl's relativity problem for M24. That is, there is no obvious way to apply exactly 24 distinct transformable coordinates (or symbol-strings) to the 24 array elements in such a way that the natural group of mediating transformations of the 24 symbol-strings is M24.
There is, however, an assignment of symbol-strings that yields a family of sets with automorphism group M24.
R.D. Carmichael in 1931 on his construction of the Steiner system S(5,8,24)–
"The linear fractional group modulo 23 of order 24•23•11 is often represented as a doubly transitive group of degree 24 on the symbols ∞, 0, 1, 2,…, 22. This transitive group contains a subgroup of order 8 each element of which transforms into itself the set ∞, 0, 1, 3, 12, 15, 21, 22 of eight elements, while the whole group transforms this set into 3•23•11 sets of eight each. This configuration of octuples has the remarkable property that any given set of five of the 24 symbols occurs in one and just one of these octuples. The largest permutation group Γ on the 24 symbols, each element of which leaves this configuration invariant, is a five-fold transitive group of degree 24 and order 24•23•22•21•20•48. This is the Mathieu group of degree 24."
— R. D. Carmichael, 1931, "Tactical Configurations of Rank Two," in American Journal of Mathematics, Vol. 53, No. 1 (Jan., 1931), pp. 217-240
For the significance of the date "February 20," see . . .
|
Google One: Gemini Advanced AI on 13 May 2024. Prompt: How can Weyl's 1946 remarks on coordinatization in "The Classical Groups" be applied to models of finite geometries? Response (after several drafts): In "The Classical Groups," Hermann Weyl discusses the concept of coordinatization, which is the process of assigning numerical coordinates to points in a geometric space. This process is fundamental in connecting abstract geometric concepts with concrete numerical representations, allowing for algebraic manipulation and analysis. Weyl's remarks on coordinatization have significant implications for models of finite geometries. Finite geometries are geometric systems with a finite number of points and lines, and they often exhibit different properties compared to traditional Euclidean geometry. Here's how Weyl's ideas can be applied to finite geometries: 1. **Relativity of Coordinatization:** Weyl emphasizes that the choice of coordinate system is arbitrary and that different coordinate systems can be used to describe the same geometric object. This relativity of coordinatization is particularly relevant in finite geometries, where multiple coordinate systems may exist, each with its own advantages and disadvantages. 2. **Equivalent Coordinatizations:** Weyl introduces the concept of "equivalent coordinatizations," which are different coordinate systems that can be transformed into one another through a group of transformations. In finite geometries, identifying and understanding these equivalent coordinatizations can provide deeper insights into the underlying structure and symmetries of the geometry. 3. **Objective Class of Coordinatizations:** Weyl discusses the problem of fixing an "objective class" of coordinatizations that capture essential features of the geometry while being independent of arbitrary choices. In finite geometries, this could involve identifying coordinatizations that best reflect the specific properties and relationships within the geometry. 4. **Group of Transformations:** Weyl emphasizes the role of the "group of transformations" that mediates between equivalent coordinatizations. In finite geometries, understanding these transformation groups can help classify different types of finite geometries and reveal their underlying symmetries. By applying Weyl's insights, researchers can gain a deeper understanding of finite geometries, including their classification, properties, and relationships. Additionally, exploring different coordinatization schemes can lead to new algebraic and geometric tools for studying finite geometries. For further exploration, you can delve into the works of other mathematicians like Steven H. Cullinane, who has written extensively on finite geometry and its connections to relativity and other areas of mathematics. I hope this explanation is helpful! Please let me know if you have any further questions. |
Update at about 5 PM ET the same day . . .
|
Prompt: Correction: Cullinane has NOT written on finite geometry's "connections to relativity." He has, instead, quoted Weyl's remarks on what Weyl himself called "the relativity problem," but what was in fact his own term for problems involving coordinatization. Such problems are of interest both in physics and in finite geometry, but the latter is a field of pure mathematics, NOT of physics. Response: You are absolutely correct. I apologize for the error in my previous response. Steven H. Cullinane has indeed quoted Weyl's remarks on "the relativity problem" in the context of finite geometry. However, as you rightly pointed out, this term refers to Weyl's own terminology for problems involving coordinatization and not the theory of relativity in physics. Finite geometry is a field of pure mathematics and does not directly connect to the physical theories of relativity. While both areas involve concepts of space and transformations, they operate in fundamentally different domains. Cullinane's work focuses on applying Weyl's insights on coordinatization to the specific challenges and structures within finite geometries. This involves exploring different coordinatization schemes, understanding their equivalences, and identifying transformation groups that reveal the underlying symmetries of finite geometries. Thank you for pointing out this important distinction. It highlights the importance of precise language and accurate attribution when discussing complex mathematical concepts. |
From The Man Who Knew Infinity to The Man Who Knew Zero.
Related mathematics: The Diamond Theorem Correlation, which
results from interchanging infinity and zero in the figure below.
"Read something that means something."
— New Yorker ad
.
Click image for
related posts.
Background — Relativity Problem in Log24.
"The class is objectively characterized, but not
the individual coordinate assignment."
Tell it to Watchduck, Hermann.
See a related remark by Quack5quack in Raiders of the Lost Coordinates.
Related material —
“The message was clear: having a finite frame of reference
creates the illusion of a world, but even the reference frame itself
is an illusion. Observers create reality, but observers aren’t real.
There is nothing ontologically distinct about an observer, because
you can always find a frame in which that observer disappears:
the frame of the frame itself, the boundary of the boundary.”
— Amanda Gefter in 2014, quoted here on Mayday 2020.
See as well, in a post from the date of Hunter Thompson’s death :
“Today, February 20, is the 19th anniversary of my note
The Relativity Problem in Finite Geometry.”
“No serious difficulty is encountered as long as one deals
with a domain consisting of a finite number of points only,
which can be ‘called up’ one after the other.” — Weyl
Background — The relativity problem in this journal.
See also this journal on November 29, 2011 —The Flight from Ennui.
Related illustration from earlier in 2011 —
See also this journal on 20 Sept. 2011 — Relativity Problem Revisited —
as well as Congregated Light.
The Hudson array mentioned above is as follows —
See also Whitehead and the
Relativity Problem (Sept. 22).
For coordinatization of a 4×4
array, see a note from 1986
in the Feb. 26 post Citation.
The exercise in the previous post was suggested by a passage
purporting to "use standard block design theory" that was written
by some anonymous author at Wikipedia on March 1, 2019:
Here "rm OR" apparently means "remove original research."
Before the March 1 revision . . .
The "original research" objected to and removed was the paragraph
beginning "To explain this further." That paragraph was put into the
article earlier on Feb. 28 by yet another anonymous author (not by me).
An account of my own (1976 and later) original research on this subject
is pictured below, in a note from Feb. 20, 1986 —
"János Bolyai was a nineteenth-century mathematician who
set the stage for the field of non-Euclidean geometry."
— Transylvania Now , October 26, 2018
From Coxeter and the Relativity Problem —
Desiring the exhilarations of changes:
The motive for metaphor, shrinking from
The weight of primary noon,
The A B C of being,
The ruddy temper, the hammer
Of red and blue, the hard sound—
Steel against intimation—the sharp flash,
The vital, arrogant, fatal, dominant X.
See as well, in this journal, Deathly Hallows, Relativity Problem, and Space Cross.
A related quote: "This is not mathematics; this is theology."
"Composed in light of both Hiroshima and
Einstein’s general theory of relativity,
Dali’s crucifixion . . . ."
— "The Crucified God: A Death in Pictures,"
by Ed Simon, April 11, 2017,
http://marginalia.lareviewofbooks.org/…
See as well Log24, The Relativity Problem at Hiroshima (Dec. 3, 2018).
Related material —
Some images, and a definition, suggested by my remarks here last night
on Apollo and Ross Douthat's remarks today on "The Return of Paganism" —
In finite geometry and combinatorics,
an inscape is a 4×4 array of square figures,
each figure picturing a subset of the overall 4×4 array:
Related material — the phrase
"Quantum Tesseract Theorem" and …
A. An image from the recent
film "A Wrinkle in Time" —
B. A quote from the 1962 book —
"There's something phoney
in the whole setup, Meg thought.
There is definitely something rotten
in the state of Camazotz."
From the former date above —
|
Saturday, September 17, 2016 |
From the latter date above —
|
Tuesday, October 18, 2016
Parametrization
|
From March 2018 —
From mathoverflow.net on Dec. 7, 2016 —
The exceptional isomorphism between
PGL(3,2) and PSL(2,7): geometric origin?
Essentially the same question was asked earlier at
math.stackexchange.com on Aug. 2, 2010.
See also this journal in November 2017 —
"Read something that means something."
— New Yorker ad
.
Background — Relativity Problem in Log24.
For example, Plato's diamond as an object to be transformed —
Versions of the transformed object —
See also The 4×4 Relativity Problem in this journal.
The term "parametrization," as discussed in Wikipedia,
seems useful for describing labelings that are not, at least
at first glance, of a vector-space nature.
Examples: The labelings of a 4×4 array by a blank space
plus the 15 two-subsets of a six-set (Hudson, 1905) or by a
blank plus the 5 elements and the 10 two-subsets of a five-set
(derived in 2014 from a 1906 page by Whitehead), or by
a blank plus the 15 line diagrams of the diamond theorem.
Thus "parametrization" is apparently more general than
the word "coodinatization" used by Hermann Weyl —
“This is the relativity problem: to fix objectively
a class of equivalent coordinatizations and to
ascertain the group of transformations S
mediating between them.”
— Hermann Weyl, The Classical Groups ,
Princeton University Press, 1946, p. 16
Note, however, that Weyl's definition of "coordinatization"
is not limited to vector-space coordinates. He describes it
as simply a mapping to a set of reproducible symbols .
(But Weyl does imply that these symbols should, like vector-space
coordinates, admit a group of transformations among themselves
that can be used to describe transformations of the point-space
being coordinatized.)
For illustrations based on the above equations, see
Coxeter and the Relativity Problem and Singer 7-Cycles .
The art above is by the Copenhagen studio
Hvass & Hannibal. For a photo of the artists,
see a webpage on Beijing Design Week 2011.
Hvass and Hannibal were apparently in Beijing
for the "open workshop," Sept. 17-23, 2011.
Gestalt-related material from this journal that week —
* Title suggested by that of a book by Quine.
See also a Log24 post on this subject from Dec. 14, 2013,
especially (scroll down) the update of March 9, 2014.
Related material on the Turyn-Curtis construction
from the University of Cambridge —
— Slide by "Dr. Parker" — Apparently Richard A. Parker —
Lecture 4, "Discovering M24," in slides for lectures 1-8 from lectures
at Cambridge in 2010-2011 on "Sporadic and Related Groups."
See also the Parker lectures of 2012-2013 on the same topic.
A third construction of Curtis's 35 4×6 1976 MOG arrays would use
Cullinane's analysis of the 4×4 subarrays' affine and projective structure,
and point out the fact that Conwell's 1910 correspondence of the 35
4+4-partitions of an 8-set with the 35 lines of the projective 3-space
over the 2-element field, PG(3, 2), is essentially the same correspondence
as that constituting Curtis's 1976 MOG.
See The Diamond Theorem, Finite Relativity, Galois Space,
Generating the Octad Generator, and The Klein Correspondence.
Update of March 22-March 23 —
Adding together as (0,1)-matrices over GF(2) the black parts (black
squares as 1's, all other squares as 0's) of the 35 4×6 arrays of the 1976
Curtis MOG would then reveal* the symmetric role played in octads
by what Curtis called the heavy brick , and so reveal also the action of
S3 on the three Curtis bricks that leaves invariant the set of all 759
octads of the S(5, 8, 24) constructed from the 35 MOG arrays. For more
details of this "by-hand" construction, see Geometry of the 4×4 Square.
For the mathematical properties of the S(5, 8, 24), it is convenient to
have a separate construction (such as Turyn's), not by hand, of the
extended binary Golay code. See the Brouwer preprint quoted above.
* "Then a miracle occurs," as in the classic 1977 Sidney Harris cartoon.
Illustration of array addition from March 23 —
For the late mathematics educator Zoltan Dienes.
“There comes a time when the learner has identified
the abstract content of a number of different games
and is practically crying out for some sort of picture
by means of which to represent that which has been
gleaned as the common core of the various activities.”
— Article by “Melanie” at Zoltan Dienes’s website
Dienes reportedly died at 97 on Jan. 11, 2014.
From this journal on that date —
A star figure and the Galois quaternion.
The square root of the former is the latter.
Update of 5:01 PM ET Feb. 6, 2014 —
An illustration by Dienes related to the diamond theorem —
See also the above 15 images in …
… and versions of the 4×4 coordinatization in The 4×4 Relativity Problem
(Jan. 17, 2014).
Profile picture of "Jo Lyxe" (Josefine Lyche) at Vimeo—
Compare to an image of Vril muse Maria Orsitsch.
From the catalog of a current art exhibition
(25 May – 31 August, 2013) in Norway,
I DE LANGE NÆTTER —
|
Josefine Lyche
Keywords (to help place my artwork in the (See also the original catalog page.) |
Clearly most of this (the non-highlighted parts) was taken
from my webpage Diamond Theory. I suppose I should be
flattered, but I am not thrilled to be associated with the
(apparently fictional) Vril Society.
For some background, see (for instance)
Conspiracy Theories and Secret Societies for Dummies .
Today's previous post on coordinate systems
suggests a look at the phrase "Galois coordinates."
A search shows that the phrase, though natural,
has apparently not been used before 2011* for solutions
to what Hermann Weyl called "the relativity problem."
A thorough historical essay on Galois coordinatization
in this sense would require more academic resources
than I have available. It would likely describe a number
of applications of Galois-field coordinates to square
(and perhaps to cubical) arrays that were studied before
1976, the date of my Diamond Theory monograph.
But such a survey might not find any such pre-1976
coordinatization of a 4×4 array by the 16 elements
of the vector 4-space over the Galois field with two
elements, GF(2).
Such coordinatizations are important because of their
close relationship to the Mathieu group M 24 .
See a preprint by Anne Taormina and Katrin Wendland,
"The overarching finite symmetry group of Kummer
surfaces in the Mathieu group M 24 ," with its remark
denying knowledge of any such coordinatization
prior to a 1989 paper by R. T. Curtis.
Related material:
Some images related to Galois coordinates, excerpted
from a Google search today (click to enlarge)—
* A rather abstract 2011 paper that uses the phrase
"Galois coordinates" may have some implications
for the naive form of the relativity problem
related to square and cubical arrays.
For the cruelest month
Click for a much larger version of the photo below.
These four Kountry Korn quartets are from the Fox Valleyaires
Men's Barbershop Chorus of Appleton, Wisconsin.
See also the fine arts here on Saturday, April 6, 2013—
The New York Times Magazine cover story
a decade ago, on Sunday, April 6, 2003:
"The artists demanded space
in tune with their aesthetic."
— "The Dia Generation,"
by Michael Kimmelman
Related material:
See Wikipedia for the difference between binary numbers
and binary coordinates from the finite Galois field GF(2).
For some background, see the relativity problem.
See also the chapter on vector spaces in Korn & Korn
(originally published by McGraw-Hill)—
.
(Continued from 1986)
|
S. H. Cullinane This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them.
— H. Weyl, The Classical Groups , In finite geometry "points" are often defined as ordered n-tuples of a finite (i.e., Galois) field GF(q). What geometric structures ("frames of reference," in Weyl's terms) are coordinatized by such n-tuples? Weyl's use of "objectively" seems to mean that such structures should have certain objective— i.e., purely geometric— properties invariant under each S. This note suggests such a frame of reference for the affine 4-space over GF(2), and a class of 322,560 equivalent coordinatizations of the frame. The frame: A 4×4 array. The invariant structure: The following set of 15 partitions of the frame into two 8-sets.
A representative coordinatization:
0000 0001 0010 0011
The group: The group AGL(4,2) of 322,560 regular affine transformations of the ordered 4-tuples over GF(2). |
S. H. Cullinane This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them.
— H. Weyl, The Classical Groups , In finite geometry "points" are often defined as ordered n-tuples of a finite (i.e., Galois) field GF(q). What geometric structures ("frames of reference," in Weyl's terms) are coordinatized by such n-tuples? Weyl's use of "objectively" seems to mean that such structures should have certain objective— i.e., purely geometric— properties invariant under each S. This note suggests such a frame of reference for the affine 4-space over GF(2), and a class of 322,560 equivalent coordinatizations of the frame. The frame: An array of 16 congruent equilateral subtriangles that make up a larger equilateral triangle. The invariant structure: The following set of 15 partitions of the frame into two 8-sets.
The group: The group AGL(4,2) of 322,560 regular affine transformations of the ordered 4-tuples over GF(2). |
For some background on the triangular version,
see the Square-Triangle Theorem,
noting particularly the linked-to coordinatization picture.
Another approach to the square-to-triangle
mapping problem (see also previous post)—
For the square model referred to in the above picture, see (for instance)
Coordinates for the 16 points in the triangular arrays
of the corresponding affine space may be deduced
from the patterns in the projective-hyperplanes array above.
This should solve the inverse problem of mapping,
in a natural way, the triangular array of 16 points
to the square array of 16 points.
Update of 9:35 AM ET July 16, 2012:
Note that the square model's 15 hyperplanes S
and the triangular model's 15 hyperplanes T —
— share the following vector-space structure —
| 0 | c | d | c + d |
| a | a + c | a + d | a + c + d |
| b | b + c | b + d | b + c + d |
| a + b | a + b + c | a + b + d | a + b + c + d |
(This vector-space a b c d diagram is from
Chapter 11 of Sphere Packings, Lattices
and Groups , by John Horton Conway and
N. J. A. Sloane, first published by Springer
in 1988.)
In memory of William S. Knowles, chiral chemist, who died last Wednesday (June 13, 2012)—
Detail from the Harvard Divinity School 1910 bookplate in yesterday morning's post—
"ANDOVER–HARVARD THEOLOGICAL LIBRARY"
Detail from Knowles's obituary in this morning's New York Times—
William Standish Knowles was born in Taunton, Mass., on June 1, 1917. He graduated a year early from the Berkshire School, a boarding school in western Massachusetts, and was admitted to Harvard. But after being strongly advised that he was not socially mature enough for college, he did a second senior year of high school at another boarding school, Phillips Academy in Andover, N.H.
Dr. Knowles graduated from Harvard with a bachelor’s degree in chemistry in 1939….
"This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them."
— Hermann Weyl, The Classical Groups, Princeton University Press, 1946, p. 16
From Pilate Goes to Kindergarten—
The six congruent quaternion actions illustrated above are based on the following coordinatization of the eightfold cube—
Problem: Is there a different coordinatization
that yields greater symmetry in the pictures of
quaternion group actions?
A paper written in a somewhat similar spirit—
"Chiral Tetrahedrons as Unitary Quaternions"—
ABSTRACT: Chiral tetrahedral molecules can be dealt [with] under the standard of quaternionic algebra. Specifically, non-commutativity of quaternions is a feature directly related to the chirality of molecules….
R.T. Curtis in a 1990 paper* discussed his method of "symmetric generation" of groups as applied to the Mathieu groups
See Finite Relativity and the Log24 posts Relativity Problem Revisited (Sept. 20) and Symmetric Generation (Sept. 21).
Here is some exposition of how this works with
* "Geometric Interpretations of the ‘Natural’ Generators of the Mathieu groups," Mathematical Proceedings of the Cambridge Philosophical Society (1990), Vol. 107, Issue 01, pp. 19-26.
Suggested by yesterday's Relativity Problem Revisited and by Cassirer on Objectivity—
From Symmetric Generation of Groups , by R.T. Curtis (Cambridge U. Press, 2007)—
"… we are saying much more than that
some set of seven involutions, which would be a very weak
requirement. We are asserting that M 24 is generated by a set
of seven involutions which possesses all the symmetries of
acting on the points of the 7-point projective plane…."
— Symmetric Generation , p. 41
"It turns out that this approach is particularly revealing and that
many simple groups, both sporadic and classical, have surprisingly
simple definitions of this type."
— Symmetric Generation , p. 42
See also (click to enlarge)—
Cassirer's remarks connect the concept of objectivity with that of object .
The above quotations perhaps indicate how the Mathieu group
"This is the moment which I call epiphany. First we recognise that the object is one integral thing, then we recognise that it is an organised composite structure, a thing in fact: finally, when the relation of the parts is exquisite, when the parts are adjusted to the special point, we recognise that it is that thing which it is. Its soul, its whatness, leaps to us from the vestment of its appearance. The soul of the commonest object, the structure of which is so adjusted, seems to us radiant. The object achieves its epiphany."
— James Joyce, Stephen Hero
For a simpler object "which possesses all the symmetries of
For symmetric generation of
Recent piracy of my work as part of a London art project suggests the following.
From http://www.trussel.com/rls/rlsgb1.htm
The 2011 Long John Silver Award for academic piracy
goes to ….
Hermann Weyl, for the remark on objectivity and invariance
in his classic work Symmetry that skillfully pirated
the much earlier work of philosopher Ernst Cassirer.
And the 2011 Parrot Award for adept academic idea-lifting
goes to …
Richard Evan Schwartz of Brown University, for his
use, without citation, of Cullinane’s work illustrating
Weyl’s “relativity problem” in a finite-geometry context.
For further details, click on the above names.
“Yo sé de un laberinto griego que es una línea única, recta.”
—Borges, “La Muerte y la Brújula”
“I know of one Greek labyrinth which is a single straight line.”
—Borges, “Death and the Compass”
Another single-line labyrinth—
Robert A. Wilson on the projective line with 24 points
and its image in the Miracle Octad Generator (MOG)—
Related material —
The remarks of Scott Carnahan at Math Overflow on October 25th, 2010
and the remarks at Log24 on that same date.
A search in the latter for miracle octad is updated below.
This search (here in a customized version) provides some context for the
Benedictine University discussion described here on February 25th and for
the number 759 mentioned rather cryptically in last night’s “Ariadne’s Clue.”
Update of March 3— For some historical background from 1931, see The Mathieu Relativity Problem.
"The cube has…13 axes of symmetry:
6 C2 (axes joining midpoints of opposite edges),
4 C3 (space diagonals), and
3C4 (axes joining opposite face centroids)."
–Wolfram MathWorld article on the cube
These 13 symmetry axes can be used to illustrate the interplay between Euclidean and Galois geometry in a cubic model of the 13-point Galois plane.
The geometer's 3×3×3 cube–
27 separate subcubes unconnected
by any Rubik-like mechanism–
The 13 symmetry axes of the (Euclidean) cube–
exactly one axis for each pair of opposite
subcubes in the (Galois) 3×3×3 cube–
A closely related structure–
the finite projective plane
with 13 points and 13 lines–
A later version of the 13-point plane
by Ed Pegg Jr.–
A group action on the 3×3×3 cube
as illustrated by a Wolfram program
by Ed Pegg Jr. (undated, but closely
related to a March 26, 1985 note
by Steven H. Cullinane)–
The above images tell a story of sorts.
The moral of the story–
Galois projective geometries can be viewed
in the context of the larger affine geometries
from which they are derived.
The standard definition of points in a Galois projective plane is that they are lines through the (arbitrarily chosen) origin in a corresponding affine 3-space converted to a vector 3-space.
If we choose the origin as the center cube in coordinatizing the 3×3×3 cube (See Weyl's relativity problem ), then the cube's 13 axes of symmetry can, if the other 26 cubes have properly (Weyl's "objectively") chosen coordinates, illustrate nicely the 13 projective points derived from the 27 affine points in the cube model.
The 13 lines of the resulting Galois projective plane may be derived from Euclidean planes through the cube's center point that are perpendicular to the cube's 13 Euclidean symmetry axes.
The above standard definition of points in a Galois projective plane may of course also be used in a simpler structure– the eightfold cube.
(The eightfold cube also allows a less standard way to picture projective points that is related to the symmetries of "diamond" patterns formed by group actions on graphic designs.)
See also Ed Pegg Jr. on finite geometry on May 30, 2006
at the Mathematical Association of America.
The current (Feb. 2009) Notices of the American Mathematical Society has a written version of Freeman Dyson's 2008 Einstein Lecture, which was to have been given in October but had to be canceled. Dyson paraphrases a mathematician on Carl Jung's theory of archetypes:
"… we do not need to accept Jung’s theory as true in order to find it illuminating."
The same is true of Jung's remarks on synchronicity.
For example —
Yesterday's entry, "A Wealth of Algebraic Structure," lists two articles– each, as it happens, related to Jung's four-diamond figure from Aion as well as to my own Notes on Finite Geometry. The articles were placed online recently by Cambridge University Press on the following dates:
R. T. Curtis's 1974 article defining his Miracle Octad Generator (MOG) was published online on Oct. 24, 2008.
Curtis's 1987 article on geometry and algebraic structure in the MOG was published online on Dec. 19, 2008.
On these dates, the entries in this journal discussed…
Oct. 24:
Cube Space, 1984-2003
Material related to that entry:
Dec. 19:
Art and Religion: Inside the White Cube
That entry discusses a book by Mark C. Taylor:
The Picture in Question: Mark Tansey and the Ends of Representation (U. of Chicago Press, 1999).
"What, then, is a frame, and what is frame work?"
One possible answer —
Hermann Weyl on the relativity problem in the context of the 4×4 "frame of reference" found in the above Cambridge University Press articles.
“From the grave, Albert Einstein poured gasoline on the culture wars between science and religion this week.
A letter the physicist wrote in 1954 to the philosopher Eric Gutkind, in which he described the Bible as ‘pretty childish’ and scoffed at the notion that the Jews could be a ‘chosen people,’ sold for $404,000 at an auction in London. That was 25 times the presale estimate.”
A less controversial Einstein-related remark:
“The relativity problem is one of central significance throughout geometry and algebra and has been recognized as such by the mathematicians at an early time.”
— Hermann Weyl, “Relativity Theory as a Stimulus in Mathematical Research,” Proceedings of the American Philosophical Society, Vol. 93, No. 7, Theory of Relativity in Contemporary Science: Papers Read at the Celebration of the Seventieth Birthday of Professor Albert Einstein in Princeton, March 19, 1949 (Dec. 30, 1949), pp. 535-541
"As noted previously, in Figure 2 viewed as a lattice the 16 digital labels 0000, 0001, etc., may be interpreted as naming the 16 subsets of a 4-set; in this case the partial ordering in the lattice is the structure preserved by the lattice's group of 24 automorphisms– the same automorphism group as that of the 16 Boolean connectives. If, however, these 16 digital labels are interpreted as naming the 16 functions from a 4-set to a 2-set (of two truth values, of two colors, of two finite-field elements, and so forth), it is not obvious that the notion of partial order is relevant. For such a set of 16 functions, the relevant group of automorphisms may be the affine group of A mentioned above. One might argue that each Venn diagram in Fig. 3 constitutes such a function– specifically, a mapping of four nonoverlapping regions within a rectangle to a set of two colors– and that the diagrams, considered simply as a set of two-color mappings, have an automorphism group of order larger than 24… in fact, of order 322,560. Whether such a group can be regarded as forming part of a 'geometry of logic' is open to debate."
The epigraph to "Finite Relativity" is:
"This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them."
— Hermann Weyl, The Classical Groups, Princeton University Press, 1946, p. 16
The added paragraph seems to fit this description.
Today is the 21st birthday of my note “The Relativity Problem in Finite Geometry.”
Some relevant quotations:
“This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them.”
— Hermann Weyl, The Classical Groups, Princeton University Press, 1946, p. 16
Describing the branch of mathematics known as Galois theory, Weyl says that it
“… is nothing else but the relativity theory for the set Sigma, a set which, by its discrete and finite character, is conceptually so much simpler than the infinite set of points in space or space-time dealt with by ordinary relativity theory.”
— Weyl, Symmetry, Princeton University Press, 1952, p. 138
Weyl’s set Sigma is a finite set of complex numbers. Some other sets with “discrete and finite character” are those of 4, 8, 16, or 64 points, arranged in squares and cubes. For illustrations, see Finite Geometry of the Square and Cube. What Weyl calls “the relativity problem” for these sets involves fixing “objectively” a class of equivalent coordinatizations. For what Weyl’s “objectively” means, see the article “Symmetry and Symmetry Breaking,” by Katherine Brading and Elena Castellani, in the Stanford Encyclopedia of Philosophy:
“The old and natural idea that what is objective should not depend upon the particular perspective under which it is taken into consideration is thus reformulated in the following group-theoretical terms: what is objective is what is invariant with respect to the transformation group of reference frames, or, quoting Hermann Weyl (1952, p. 132), ‘objectivity means invariance with respect to the group of automorphisms [of space-time].‘[22]
22. The significance of the notion of invariance and its group-theoretic treatment for the issue of objectivity is explored in Born (1953), for example. For more recent discussions see Kosso (2003) and Earman (2002, Sections 6 and 7).
References:
Born, M., 1953, “Physical Reality,” Philosophical Quarterly, 3, 139-149. Reprinted in E. Castellani (ed.), Interpreting Bodies: Classical and Quantum Objects in Modern Physics, Princeton, NJ: Princeton University Press, 1998, pp. 155-167.
Earman, J., 2002, “Laws, Symmetry, and Symmetry Breaking; Invariance, Conservation Principles, and Objectivity,’ PSA 2002, Proceedings of the Biennial Meeting of the Philosophy of Science Association 2002, forthcoming [Abstract/Preprint available online]
Kosso, P., 2003, “Symmetry, objectivity, and design,” in K. Brading and E. Castellani (eds.), Symmetries in Physics: Philosophical Reflections, Cambridge: Cambridge University Press, pp. 410-421.
Weyl, H., 1952, Symmetry, Princeton, NJ: Princeton University Press.
See also
Archives Henri Poincaré (research unit UMR 7117, at Université Nancy 2, of the CNRS)–
“Minkowski, Mathematicians, and the Mathematical Theory of Relativity,” by Scott Walter, in The Expanding Worlds of General Relativity (Einstein Studies, volume 7), H. Goenner, J. Renn, J. Ritter and T. Sauer, editors, Boston/Basel: Birkhäuser, 1999, pp. 45-86–
“Developing his ideas before Göttingen mathematicians in April 1909, Klein pointed out that the new theory based on the Lorentz group (which he preferred to call ‘Invariantentheorie’) could have come from pure mathematics (1910: 19). He felt that the new theory was anticipated by the ideas on geometry and groups that he had introduced in 1872, otherwise known as the Erlangen program (see Gray 1989: 229).”
References:
Gray, Jeremy J. (1989). Ideas of Space. 2d ed. Oxford: Oxford University Press.
Klein, Felix. (1910). “Über die geometrischen Grundlagen der Lorentzgruppe.” Jahresbericht der deutschen Mathematiker-Vereinigung 19: 281-300. [Reprinted: Physikalische Zeitschrift 12 (1911): 17-27].
Related material: A pathetically garbled version of the above concepts was published in 2001 by Harvard University Press. See Invariances: The Structure of the Objective World, by Robert Nozick.
Serious
"I don't think the 'diamond theorem' is anything serious, so I started with blitzing that."
— Charles Matthews at Wikipedia, Oct. 2, 2006
"The 'seriousness' of a mathematical theorem lies, not in its practical consequences, which are usually negligible, but in the significance of the mathematical ideas which it connects. We may say, roughly, that a mathematical idea is 'significant' if it can be connected, in a natural and illuminating way, with a large complex of other mathematical ideas."
— G. H. Hardy, A Mathematician's Apology
Matthews yesterday deleted references to the diamond theorem and related material in the following Wikipedia articles:
Affine group
Reflection group
Symmetry in mathematics
Incidence structure
Invariant (mathematics)
Symmetry
Finite geometry
Group action
History of geometry
This would appear to be a fairly large complex of mathematical ideas.
See also the following "large complex" cited, following the above words of Hardy, in Diamond Theory:
Affine geometry, affine planes, affine spaces, automorphisms, binary codes, block designs, classical groups, codes, coding theory, collineations, combinatorial, combinatorics, conjugacy classes, the Conwell correspondence, correlations, design theory, duads, duality, error correcting codes, exceptional groups, finite fields, finite geometry, finite groups, finite rings, Galois fields, generalized quadrangles, generators, geometry, GF(2), GF(4), the (24,12) Golay code, group actions, group theory, Hadamard matrices, hypercube, hyperplanes, hyperspace, incidence structures, invariance, Karnaugh maps, Kirkman's schoolgirl problem, Latin squares, Leech lattice, linear groups, linear spaces, linear transformations, Mathieu groups, matrix theory, Meno, Miracle Octad Generator, MOG, multiply transitive groups, octads, the octahedral group, orthogonal arrays, outer automorphisms, parallelisms, partial geometries, permutation groups, PG(3,2), polarities, Polya-Burnside theorem, projective geometry, projective planes, projective spaces, projectivities, Reed-Muller codes, the relativity problem, Singer cycle, skew lines, sporadic simple groups, Steiner systems, symmetric, symmetry, symplectic, synthemes, synthematic, tesseract, transvections, Walsh functions, Witt designs.
New Site
(Site title and address were revised on May 21, 2006.)
The new site for my math files is
finitegeometry.org/sc/index.html:
 |
Finite Geometry |
|
This site is about the (the mathematical structure, |
|
As time goes on, I'll be changing links on the Web to my math pages, which are now scattered at various Web addresses, to refer to this new site.
Incidentally, this is the 20th anniversary of my note, "The relativity problem in finite geometry."
Earendil_Silmarils:
Les Anamorphoses:
"Pour construire un dessin en perspective,
le peintre trace sur sa toile des repères:
la ligne d'horizon (1),
le point de fuite principal (2)
où se rencontre les lignes de fuite (3)
et le point de fuite des diagonales (4)."
_______________________________
Serge Mehl,
Perspective &
Géométrie Projective:
"… la géométrie projective était souvent
synonyme de géométrie supérieure.
Elle s'opposait à la géométrie
euclidienne: élémentaire…
La géométrie projective, certes supérieure
car assez ardue, permet d'établir
de façon élégante des résultats de
la géométrie élémentaire."
Similarly…
Finite projective geometry
(in particular, Galois geometry)
is certainly superior to
the elementary geometry of
quilt-pattern symmetry
and allows us to establish
de façon élégante
some results of that
elementary geometry.
Other Related Material…
from algebra rather than
geometry, and from a German
rather than from the French:
"This is the relativity problem:
to fix objectively a class of
equivalent coordinatizations
and to ascertain
the group of transformations S
mediating between them."
— Hermann Weyl,
The Classical Groups,
Princeton U. Press, 1946
Evariste Galois
Weyl also says that the profound branch
of mathematics known as Galois theory
"Perhaps every science must
start with metaphor
and end with algebra;
and perhaps without metaphor
there would never have been
any algebra."
For metaphor and
algebra combined, see
A.M.S. abstract 79T-A37,
Notices of the
American Mathematical Society,
February 1979, pages A-193, 194 —
the original version of the 4×4 case
of the diamond theorem.
"When approaching unfamiliar territory, we often, as observed earlier, try to describe or frame the novel situation using metaphors based on relations perceived in a familiar domain, and by using our powers of association, and our ability to exploit the structural similarity, we go on to conjecture new features for consideration, often not noticed at the outset. The metaphor works, according to Max Black, by transferring the associated ideas and implications of the secondary to the primary system, and by selecting, emphasising and suppressing features of the primary in such a way that new slants on it are illuminated."
— Paul Thompson, University College, Oxford,
The Nature and Role of Intuition
in Mathematical Epistemology
That intuition, metaphor (i.e., analogy), and association may lead us astray is well known. The examples of French perspective above show what might happen if someone ignorant of finite geometry were to associate the phrase "4×4 square" with the phrase "projective geometry." The results are ridiculously inappropriate, but at least the second example does, literally, illuminate "new slants"– i.e., diagonals– within the perspective drawing of the 4×4 square.
Similarly, analogy led the ancient Greeks to believe that the diagonal of a square is commensurate with the side… until someone gave them a new slant on the subject.
Relativity Blues
Today, February 20, is the 19th anniversary of my note The Relativity Problem in Finite Geometry. Here is some related material.
In 1931, the Christian writer Charles Williams grappled with the theology of time, space, free will, and the many-worlds interpretation of quantum mechanics (anticipating by many years the discussion of this topic by physicists beginning in the 1950's).
(Some pure mathematics — untainted by physics or theology — that is nevertheless related, if only by poetic analogy, to Williams's 1931 novel, Many Dimensions, is discussed in the above-mentioned note and in a generalization, Solomon's Cube.)
On the back cover of Williams's 1931 novel, the current publisher, William B. Eerdmans Publishing Company of Grand Rapids, Michigan, makes the following statement:
"Replete with rich religious imagery, Many Dimensions explores the relation between predestination and free will as it depicts different human responses to redemptive transcendence."
One possible response to such statements was recently provided in some detail by a Princeton philosophy professor. See On Bullshit, by Harry G. Frankfurt, Princeton University Press, 2005.
A more thoughtful response would take into account the following:
1. The arguments presented in favor of philosopher John Calvin, who discussed predestination, in The Death of Adam: Essays on Modern Thought, by Marilynne Robinson
2. The physics underlying Einstein's remarks on free will, God, and dice
3. The physics underlying Rebecca Goldstein's novel Properties of Light and Paul Preuss's novels Secret Passages and Broken Symmetries
4. The physics underlying the recent so-called "free will theorem" of John Conway and Simon Kochen of Princeton University
5. The recent novel Gilead, by Marilynne Robinson, which deals not with philosophy, but with lives influenced by philosophy — indirectly, by the philosophy of the aforementioned John Calvin.
From a review of Gilead by Jane Vandenburgh:
"In The Death of Adam, Robinson shows Jean Cauvin to be the foremost prophet of humanism whose Protestant teachings against the hierarchies of the Roman church set in motion the intellectual movements that promoted widespread literacy among the middle and lower classes, led to both the American and French revolutions, and not only freed African slaves in the United States but brought about suffrage for women. It's odd then that through our culture's reverse historicism, the term 'Calvinism' has come to mean 'moralistic repression.'"
For more on what the Calvinist publishing firm Eerdmans calls "redemptive transcendence," see various July 2003 Log24.net entries. If these entries include a fair amount of what Princeton philosophers call bullshit, let the Princeton philosophers meditate on the summary of Harvard philosophy quoted here on November 5 of last year, as well as the remarks of November 5, 2003, and those of November 5, 2002.
From Many Dimensions (Eerdmans paperback, 1963, page 53):
"Lord Arglay had a suspicion that the Stone would be purely logical. Yes, he thought, but what, in that sense, were the rules of its pure logic?"
A recent answer:
"We symbolize logical necessity
with the box 
)
and logical possibility
with the diamond 
).
— Keith Allen Korcz,
(Log24.net, 1/25/05)
And what do we
symbolize by 
?
"The possibilia that exist,
and out of which
the Universe arose,
are located in
a necessary being…."
— Michael Sudduth,
Notes on
God, Chance, and Necessity
by Keith Ward,
Regius Professor of Divinity
at Christ Church College, Oxford
(the home of Lewis Carroll)
Finite Relativity
Today is the 18th birthday of my note
“The Relativity Problem in Finite Geometry.”
That note begins with a quotation from Weyl:
“This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them.”
— Hermann Weyl, The Classical Groups, Princeton University Press, 1946, p. 16
Here is another quotation from Weyl, on the profound branch of mathematics known as Galois theory, which he says
“… is nothing else but the relativity theory for the set Sigma, a set which, by its discrete and finite character, is conceptually so much simpler than the infinite set of points in space or space-time dealt with by ordinary relativity theory.”
— Weyl, Symmetry, Princeton University Press, 1952, p. 138
This second quotation applies equally well to the much less profound, but more accessible, part of mathematics described in Diamond Theory and in my note of Feb. 20, 1986.
Powered by WordPress
