A Logocentric Archetype
Today we examine the relativist, nominalist, leftist, nihilist, despairing, depressing, absurd, and abominable work of Samuel Beckett, darling of the postmodernists.
One lens through which to view Beckett is an essay by Jennifer Martin, "Beckettian Drama as Protest: A Postmodern Examination of the 'Delogocentering' of Language." Martin begins her essay with two quotations: one from the contemptible French twerp Jacques Derrida, and one from Beckett's masterpiece of stupidity, Molloy. For a logocentric deconstruction of Derrida, see my note, "The Shining of May 29," which demonstrates how Derrida attempts to convert a rather important mathematical result to his brand of nauseating and pretentious nonsense, and of course gets it wrong. For a logocentric deconstruction of Molloy, consider the following passage:
"I took advantage of being at the seaside to lay in a store of sucking-stones. They were pebbles but I call them stones…. I distributed them equally among my four pockets, and sucked them turn and turn about. This raised a problem which I first solved in the following way. I had say sixteen stones, four in each of my four pockets these being the two pockets of my trousers and the two pockets of my greatcoat. Taking a stone from the right pocket of my greatcoat, and putting it in my mouth, I replaced it in the right pocket of my greatcoat by a stone from the right pocket of my trousers, which I replaced by a stone from the left pocket of my trousers, which I replaced by a stone from the left pocket of my greatcoat, which I replaced by the stone which was in my mouth, as soon as I had finished sucking it. Thus there were still four stones in each of my four pockets, but not quite the same stones….But this solution did not satisfy me fully. For it did not escape me that, by an extraordinary hazard, the four stones circulating thus might always be the same four."
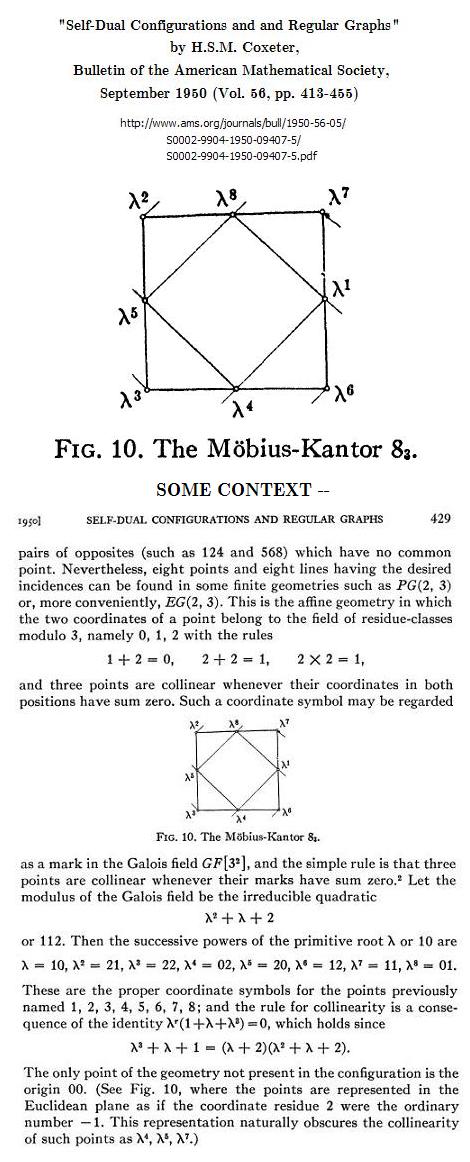
Beckett is describing, in great detail, how a damned moron might approach the extraordinarily beautiful mathematical discipline known as group theory, founded by the French anticleric and leftist Evariste Galois. Disciples of Derrida may play at mimicking the politics of Galois, but will never come close to imitating his genius. For a worthwhile discussion of permutation groups acting on a set of 16 elements, see R. D. Carmichael's masterly work, Introduction to the Theory of Groups of Finite Order, Ginn, Boston, 1937, reprinted by Dover, New York, 1956.
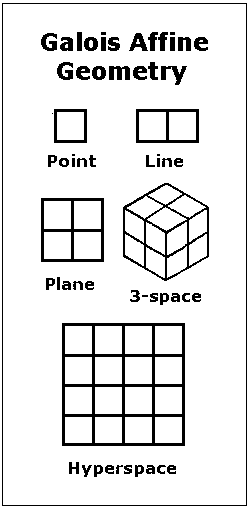
There are at least two ways of approaching permutations on 16 elements in what Pascal calls "l'esprit géométrique." My website Diamond Theory discusses the action of the affine group in a four-dimensional finite geometry of 16 points. For a four-dimensional euclidean hypercube, or tesseract, with 16 vertices, see the highly logocentric movable illustration by Harry J. Smith. The concept of a tesseract was made famous, though seen through a glass darkly, by the Christian writer Madeleine L'Engle in her novel for children and young adults, A Wrinkle in Tme.
This tesseract may serve as an archetype for what Pascal, Simone Weil (see my earlier notes), Harry J. Smith, and Madeleine L'Engle might, borrowing their enemies' language, call their "logocentric" philosophy.
For a more literary antidote to postmodernist nihilism, see Archetypal Theory and Criticism, by Glen R. Gill.
For a discussion of the full range of meaning of the word "logos," which has rational as well as religious connotations, click here.