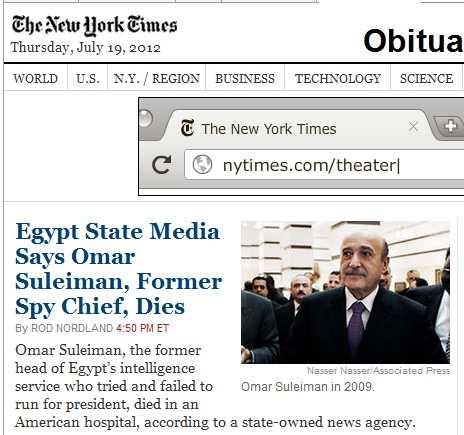
Cut to the Chase.

“1 + 2 + 3 + … = –1/12.”
Robin Williams and the Stages of Math
i) shock & denial
ii) anger
iii) bargaining
iv) depression
v) acceptance
And then…
vi) checking
vii) Joan Rivers:

Two items from the August 5, 2005, anniversary
of the day Marilyn Monroe was found dead—
2. Literary Symbol —
See also related material on Hollywood.
Leg-Pulling
 |
"… to make the author manifestly unreliable"
Not to mention the reader.
Related material —
"Democrats– in conclusion– Democrats in America
were put on earth to do one thing– Drag the
ignorant hillbilly half of this country into the next
century, which in their case is the 19th."
Reply to Maher:
"Hell is other people."
— Jean-Paul Sartre
|
Related material: Dragging Maher into the 18th century– From
Related material– Lemniscate to Langlands (2004) |
The books pictured above are From Discrete to Continuous ,
by Katherine Neal, and Geometrical Landscapes , by Amir Alexander.
Commentary—
“Harriot has given no indication of how to resolve
such problems, but he has pasted in in English,
at the bottom of his page, these three enigmatic
lines:
‘Much ado about nothing.
Great warres and no blowes.
Who is the foole now?’
Harriot’s sardonic vein of humour, and the subtlety of
his logical reasoning still have to receive their full due.”
— “Minimum and Maximum, Finite and Infinite:
Bruno and the Northumberland Circle,” by Hilary Gatti,
Journal of the Warburg and Courtauld Institutes ,
Vol. 48 (1985), pp. 144-163
|
Cullinane Diamond Theorem Research Report by https://you.com/?chatMode=research on March 3, 2024 Overview of the Cullinane Diamond Theorem The Cullinane Diamond Theorem is a mathematical concept developed by Steven H. Cullinane that explores the symmetrical properties of certain geometric patterns. It is particularly concerned with the structure of finite projective geometry as it relates to the 35 square patterns found in R. T. Curtis's Miracle Octad Generator (MOG). The theorem asserts that every G-image of a diamond figure D possesses some form of ordinary or color-interchange symmetry. Symmetry and Group Theory The theorem is deeply rooted in group theory, with G being isomorphic to the affine group A on the linear 4-space over the finite field GF(2). This group has a significant order of 322,560 and underlies the symmetry of both the diamond-theorem figures and the square patterns of the MOG . The 35 structures of the 840 G-images of D are isomorphic to the 35 lines in the 3-dimensional projective space over GF(2), which explains the symmetry of the line diagrams and the two-color patterns. The Diamond Theorem in Various Dimensions The diamond theorem can be applied to different cases, such as the 4×4, 2×2, and even 3-dimensional cubes like the 2x2x2 and 4x4x4 cubes. The generalized statement of the theorem involves inscribing a white diamond in a black square and dividing it into four quadrants, each with a diagonal split into black and white halves. Algebraic Implications The theorem has algebraic implications, such as the ability to express every 4-coloring as a sum of three 2-colorings. This algebraic formulation is useful for demonstrating that certain four-colored graphic images can form a ring under multiplication. There is also an infinite family of such 'diamond' rings, isomorphic to rings of matrices over GF(4). Philosophical and Cultural Context Steven H. Cullinane has also explored the philosophical implications of the diamond theorem, referring to it in the context of Plato's Meno dialogue and opposing it to the 'Story Theory of truth' as discussed by Richard J. Trudeau. The theorem is seen as a correct statement of the relation between geometry and the physical universe. Clarification on Cullinan Diamonds It is important to note that the Cullinane Diamond Theorem is unrelated to the Cullinan diamond, which is a famous large gemstone discovered in South Africa and now part of the British Crown Jewels. The Cullinan diamond has its own historical and cultural significance, with its various cut shapes and ownership history. In summary, the Cullinane Diamond Theorem is a mathematical concept that reveals the symmetrical properties of certain geometric patterns, with applications in group theory and algebra. It also has philosophical implications, drawing connections to classical ideas about truth and geometry. |
Instagram ad for You.com AI in research mode
"Show me ALL your sources, babe."
— Line adapted from Leonardo DiCaprio
From some Canadian legal boilerplate —
E. Be able to provide complete, clean, unencumbered
chain of title for the Project, must have all the rights,
releases and clearances necessary to produce, own and
exploit the Project and for deployment of the Project . . . .
Weak Links in the Chain of Title —
A 2006 biography of geometer H.S.M. Coxeter:
The Aleph (implicit in a 1950 article by Coxeter):
Click on images
for further details.

From Chomsky's remarks in The New York Times today —
"It is at once comic and tragic, as Borges might have noted,
that so much money and attention should be concentrated
on so little a thing — something so trivial when contrasted
with the human mind, which by dint of language, in the
words of Wilhelm von Humboldt, can make 'infinite use of
finite means,' creating ideas and theories with universal reach."
A search in this journal for Humboldt University yields . . .
"Cum grano salis" — Boris Karloff in "The Black Cat."
From tonight's previous post —
"here I come again . . . the square root of minus one,
having terminated my humanities" —
Samuel Beckett, Stories and Texts for Nothing
(New York: Grove, 1967), 128.
|
From The French Mathematician 0
I had foreseen it all in precise detail. i = an imaginary being
Here, on this complex space, |
Related reading . . .
See also "William Lawvere, Category Theory, Hegel, Mao, and Code."
( https://www.reddit.com/r/socialistprogrammers/comments/m1oe88/
william_lawvere_category_theory_hegel_mao_and_code/ )
Also relating category theory and computation —
the interests of Lawvere and those of Davis — is
an article at something called The Topos Institute (topos.site) —
"Computation and Category Theory," by Joshua Meyers,
Wednesday, 10 Aug., 2022.
Meyers on Davis —
"The novelist Cormac McCarthy has been a fixture around
the Santa Fe Institute since its embryonic stages in the
early 1980s. Cormac received a MacArthur Award in 1981
and met one of the members of the board of the MacArthur
Foundation, Murray Gell-Mann, who had won the Nobel Prize
in physics in 1969. Cormac and Murray discovered that they
shared a keen interest in just about everything under the sun
and became fast friends. When Murray helped to found the
Santa Fe Institute in 1984, he brought Cormac along, knowing
that everyone would benefit from this cross-disciplinary
collaboration." — https://www.santafe.edu/news-center/news/
cormac-and-sfi-abiding-friendship
Joy Williams, review of two recent Cormac McCarthy novels —
"McCarthy has pocketed his own liturgical, ecstatic style
as one would a coin, a ring, a key, in the service of a more
demanding and heartless inquiry through mathematics and
physics into the immateriality, the indeterminacy, of reality."
A Demanding and Heartless Coin, Ring, and Key:
COIN

RING
"We can define sums and products so that the G-images of D generate
an ideal (1024 patterns characterized by all horizontal or vertical "cuts"
being uninterrupted) of a ring of 4096 symmetric patterns. There is an
infinite family of such 'diamond' rings, isomorphic to rings of matrices
over GF(4)."
KEY
"It must be remarked that these 8 heptads are the key to an elegant proof…."
— Philippe Cara, "RWPRI Geometries for the Alternating Group A8," in
Finite Geometries: Proceedings of the Fourth Isle of Thorns Conference
(July 16-21, 2000), Kluwer Academic Publishers, 2001, ed. Aart Blokhuis,
James W. P. Hirschfeld, Dieter Jungnickel, and Joseph A. Thas, pp. 61-97.
For those who prefer a "liturgical, ecstatic style" —

Click the above galaxy for a larger image.
"O God, I could be bounded in a nutshell
and count myself a king of infinite space,
were it not that I have bad dreams." — Hamlet
Battle of the Nutshells —
From a much larger nutshell
on the above code date—
Update of 11:30 AM ET April 1, 2022 — A simpler version:
The above picture may be used to to introduce the concept of a "shape constant"
in similar figures — like the shape constant pi in a circle or the square root of 2
in a square. In each of the three similar figures at right above, the ratio of the
triangular area to the area of the attached square is a shape constant …
the same, because of their similarity, for each of the three shapes. Since the
areas of the top two triangles at right sum to that of the enclosed triangle at left,
their attached square areas sum to the area of the bottom square, Q.E.D.
The source of the proof —
Note the book subtitle below: "minutes from an infinite paradise."

For further details, see other posts tagged Revelado.
Hans Freudenthal in 1962 on the axiomatic approach to geometry
of Fano and Hilbert —
"The bond with reality is cut."

Some philosophical background —

For Weyl's "few isolated relational concepts," see (for instance)
Projective Geometries over Finite Fields , by
J. W. P. Hirschfeld (first published by Oxford University Press in 1979).
Weyl in 1932 —
|
Mathematics is the science of the infinite , its goal the symbolic comprehension of the infinite with human, that is finite, means. It is the great achievement of the Greeks to have made the contrast between the finite and the infinite fruitful for the cognition of reality. The intuitive feeling for, the quiet unquestioning acceptance of the infinite, is peculiar to the Orient; but it remains merely an abstract consciousness, which is indifferent to the concrete manifold of reality and leaves it unformed, unpenetrated. Coming from the Orient, the religious intuition of the infinite, the apeiron , takes hold of the Greek soul in the Dionysiac-Orphic epoch which precedes the Persian wars. Also in this respect the Persian wars mark the separation of the Occident from the Orient. This tension between the finite and the infinite and its conciliation now become the driving motive of Greek investigation; but every synthesis, when it has hardly been accomplished, causes the old contrast to break through anew and in a deepened sense. In this way it determines the history of theoretical cognition to our day. — "The Open World: Three Lectures on the Metaphysical Implications of Science," 1932 |
The "secret, subterranean river" of Shulevitz is
a flow of thought favorable to the cause of feminism,
but not necessarily to other "revolutionary" ideas.
Compare and contrast:
"Where Alph, the sacred river, ran"
— Coleridge, Kubla Khan
"Where Aleph the sacred symbol ran"
— Cullinane, "The Coxeter Aleph"
For group discussion:
How (if at all) is the "finitude" of Heidegger related to
mathematical finitude and The King of Infinite Space ?
From this journal on Nov. 9-12, 2004:
|
Fade to Black “…that ineffable constellation of talents that makes the player of rank: a gift for conceiving abstract schematic possibilities; a sense of mathematical poetry in the light of which the infinite chaos of probability and permutation is crystallized under the pressure of intense concentration into geometric blossoms; the ruthless focus of force on the subtlest weakness of an opponent.” — Trevanian, Shibumi “‘Haven’t there been splendidly elegant colors in Japan since ancient times?’ ‘Even black has various subtle shades,’ Sosuke nodded.” — Yasunari Kawabata, The Old Capital An Ad Reinhardt painting described in the entry of
Ad Reinhardt, Abstract Painting, 1960-66. The viewer may need to tilt the screen to see that “The grid is a staircase to the Universal…. We could think about Ad Reinhardt, who, despite his repeated insistence that ‘Art is art,’ ended up by painting a series of… nine-square grids in which the motif that inescapably emerges is a Greek cross.  Greek Cross There is no painter in the West who can be unaware of the symbolic power of the cruciform shape and the Pandora’s box of spiritual reference that is opened once one uses it.” — “Grids,” by Rosalind Krauss, |
Related material from The New York Times today —
With apologies to those readers unable to follow knight moves .
The Queen's Gambit , by Walter Tevis,
published Feb. 1983 —
“Would you care for a cocktail?” he asked pleasantly.
She looked around her at the quiet restaurant,
at the people eating lunch, at the table with desserts
near the velvet rope at the entrance to the dining room.
“A Gibson,” she said. “On the rocks.”
"A silver tide of phosphenes boiled across my field of vision
as the matrix began to unfold in my head, a 3-D chessboard,
infinite and perfectly transparent."
"'Rikki Don't Lose That Number' is a single
released in 1974 by rock/jazz rock group Steely Dan
and the opening track of their third album Pretzel Logic .
It was the most successful single of the group's career,
peaking at number 4 on the Billboard Hot 100 in
the summer of 1974." — Wikipedia
Brian Harley, Mate in Two Moves , 1931—
“The key is the cocktail that begins the proceedings.”

See as well my post "Introduction to Cyberspace" (May 26, 2020).
In memory of Wilford Brimley:
“The polymorphic Thing, capable of absorbing the human
as but one among other morphological possibilities in its
seemingly infinite repertoire, can be understood, that is,
as the embodiment of evolution.”
— Eric White, Science Fiction Studies #61 (Vol. 20, Part 3, Nov. 1993),
“The Erotics of Becoming: XENOGENESIS and The Thing“

|
" Lying at the axis of everything, zero is both real and imaginary. Lovelace was fascinated by zero; as was Gottfried Leibniz, for whom, like mathematics itself, it had a spiritual dimension. It was this that let him to imagine the binary numbers that now lie at the heart of computers: 'the creation of all things out of nothing through God's omnipotence, it might be said that nothing is a better analogy to, or even demonstration of such creation than the origin of numbers as here represented, using only unity and zero or nothing.' He also wrote, 'The imaginary number is a fine and wonderful recourse of the divine spirit, almost an amphibian between being and nonbeing.' "
— A footnote from page 229 of Sydney Padua's |
A related passage —
|
From The French Mathematician 0
I had foreseen it all in precise detail. i = an imaginary being
Here, on this complex space, |
Hume, from posts tagged "four-set" in this journal —
"The mind is a kind of theatre, where several perceptions
successively make their appearance; pass, repass, glide away,
and mingle in an infinite variety of postures and situations.
There is properly no simplicity in it at one time, nor identity
in different, whatever natural propension we may have
to imagine that simplicity and identity."
Paz, from a search for Paz + Identity in this journal —
|
"At the point of convergence by Octavio Paz, translated by Helen Lane
|
The above reading was suggested by a post of
New Year's Day, Jan. 1, 2013 — The Simplest Situation.
See also Ahem (Sunday morning, Dec. 10, 2017).
From a post last month —
"You're gonna need a bigger boat."
— Roy Scheider in "Jaws"
"We're gonna need more holy water."
— "Season of the Witch"
… and for Tom Hanks, Dan Brown, and Francine Prose —
From a search in this journal for "More Holy Water" —
A post of January 7, 2011, has the following:
"Infinite Jest… now stands as the principal contender
for what serious literature can aspire to
in the late twentieth and early twenty-first centuries."
— All Things Shining, a work of pop philosophy
published January 4th
"You're gonna need a bigger boat."
— Roy Scheider in "Jaws"
"We're gonna need more holy water."
— "Season of the Witch"
A post suggested by the word tzimtzum (see Wednesday)
or tsimtsum (see this morning) —
Lifeboat from the Tsimtsum in Life of Pi —

Another sort of tsimtsum, contracting infinite space to a finite space —
"Much like the irrational number pi,
the primal tsimtsum transforms
an infinite circle into a measured line."
— Tzvi Freeman at Chabad.org
The College Mathematics Journal , 46, No. 3 (May 2015), pp. 162–171
From "The Most Notorious Section Phrases," by Sophie G. Garrett
in The Harvard Crimson on April 5, 2017 —
This passage reminds me of (insert impressive philosophy
that was not in the reading).
This student is just being a show off. We get that they are smart
and well read. Congrats, but please don’t make the rest of the us
look bad in comparison. It should be enough to do the assigned
reading without making connections to Hume’s theory of the self.
Hume on personal identity (the "self") —
|
For my part, when I enter most intimately into what I call myself, I always stumble on some particular perception or other, of heat or cold, light or shade, love or hatred, pain or pleasure. I never can catch myself at any time without a perception, and never can observe any thing but the perception. When my perceptions are removed for any time, as by sound sleep, so long am I insensible of myself, and may truly be said not to exist. And were all my perceptions removed by death, and could I neither think, nor feel, nor see, nor love, nor hate, after the dissolution of my body, I should be entirely annihilated, nor do I conceive what is further requisite to make me a perfect nonentity. I may venture to affirm of the rest of mankind, that they are nothing but a bundle or collection of different perceptions, which succeed each other with an inconceivable rapidity, and are in a perpetual flux and movement. Our eyes cannot turn in their sockets without varying our perceptions. Our thought is still more variable than our sight; and all our other senses and faculties contribute to this change: nor is there any single power of the soul, which remains unalterably the same, perhaps for one moment. The mind is a kind of theatre, where several perceptions successively make their appearance; pass, repass, glide away, and mingle in an infinite variety of postures and situations. There is properly no simplicity in it at one time, nor identity in different, whatever natural propension we may have to imagine that simplicity and identity. The comparison of the theatre must not mislead us. They are the successive perceptions only, that constitute the mind; nor have we the most distant notion of the place where these scenes are represented, or of the materials of which it is composed. |
Related material —
Imago Dei in this journal.
Backstory —
The previous post
and The Crimson Abyss.
The “inarticulate” image from last night’s
“Raid on the Inarticulate” —
This is, in a sense, an island of nothing in a sea of being.
Contrast with an opposite image in Wittgenstein’s “Diktat für Schlick”:
| From The Voices of Wittgenstein: The Vienna Circle , ed. by Gordon Baker, first published by Routledge in 2003. From Ch. 1, “Dictation for Schlick” — p. 69 — |
“Ripples spread from castle rock ….” — “Endgame,” 1986
From Models and Metaphors , by Max Black,
Cornell University Press, 1962 —

I do not recommend the work of Lewin, nor that of a later
science groupie, Keith Devlin.
In September 2014, Devlin wrote an ignorant column about
a sort of bad mathematical joke based on a divergent infinite series.
He has now returned to the topic, this time writing more about
its proper mathematical background: analytic continuation .
Lewin is to Devlin as Lévi-Strauss is to Chomsky.
None of these four should be taken very seriously.
Max Black, however, should .
The title is from a post of last Thursday afternoon — Dec. 8, 2016.
An image from that post appeared here last year —
See also philosophy notes from Infinite Jest .
Some backstory —
See also, from that same day, "24-Part Invention."
* The title is a reference to a 2001 article by Cartier on
"the evolution of concepts of space and symmetry" —
A prequel to the 2013 film "The Zero Theorem" —
"Down below, infinitely deep into the blackness,
things were beginning. The blackness had
arranged itself into a whirlpool…."
— Peter Dickinson, A Box of Nothing (1985),
"Chapter 19: Star Tree"
— may serve as a sequel to the life of the book's author.
(See Dickinson Sequel in this journal.)
"O God, I could be bounded in a nutshell
and count myself a king of infinite space,
were it not that I have bad dreams." — Hamlet
The New York Review of Books , in a review
of two books on video games today, quotes an author
who says that the Vikings believed the sky to be
“the blue skull of a giant.”
See as well posts tagged The Nutshell.
An image that led off the year-end review yesterday in
the weblog of British combinatorialist Peter J. Cameron:
See also this weblog's post final post of 2014,
with a rectangular array illustrating the six faces
of a die, and Cameron's reference yesterday to
a die-related post…
"The things on my blog that seem to be
of continuing value are the expository
series like the one on the symmetric group
(the third post in this series was reblogged
by Gil Kalai last month, which gave it a new
lease of life)…."
A tale from an author of Prague:
| The Emperor—so they say—has sent a message, directly from his death bed, to you alone, his pathetic subject, a tiny shadow which has taken refuge at the furthest distance from the imperial sun. He ordered the herald to kneel down beside his bed and whispered the message into his ear. He thought it was so important that he had the herald repeat it back to him. He confirmed the accuracy of the verbal message by nodding his head. And in front of the entire crowd of those who’ve come to witness his death—all the obstructing walls have been broken down and all the great ones of his empire are standing in a circle on the broad and high soaring flights of stairs—in front of all of them he dispatched his herald. The messenger started off at once, a powerful, tireless man. Sticking one arm out and then another, he makes his way through the crowd. If he runs into resistance, he points to his breast where there is a sign of the sun. So he moves forward easily, unlike anyone else. But the crowd is so huge; its dwelling places are infinite. If there were an open field, how he would fly along, and soon you would hear the marvelous pounding of his fist on your door. But instead of that, how futile are all his efforts. He is still forcing his way through the private rooms of the innermost palace. He will never he win his way through. And if he did manage that, nothing would have been achieved. He would have to fight his way down the steps, and, if he managed to do that, nothing would have been achieved. He would have to stride through the courtyards, and after the courtyards the second palace encircling the first, and, then again, stairs and courtyards, and then, once again, a palace, and so on for thousands of years. And if he finally did burst through the outermost door—but that can never, never happen—the royal capital city, the centre of the world, is still there in front of him, piled high and full of sediment. No one pushes his way through here, certainly not with a message from a dead man. But you sit at your window and dream of that message when evening comes. |
See also a passage quoted in this weblog on the original
date of Cameron's Prague image, July 26, 2014 —
"The philosopher Graham Harman is invested in
re-thinking the autonomy of objects and is part
of a movement called Object-Oriented-Philosophy
(OOP)." — From “The Action of Things,” a 2011
M.A. thesis at the Center for Curatorial Studies,
Bard College, by Manuela Moscoso
— in the context of a search here for the phrase
"structure of the object." An image from that search:
Robin Williams and the Stages of Math
i) shock & denial
ii) anger
iii) bargaining
iv) depression
v) acceptance
And then…
vi) checking
vii) Joan Rivers

See also

The previous post, Infinite Jest, suggests
a midrash on “–1/12” (i.e., minus one-twelfth):
Here and at Catholics for Classical Education.
See also Tom Wolfe on manifestos —

— and part of an interesting Sept. 2, 2014, manifesto by
Common Core supporter Keith Devlin:
“Graduate students of mathematics are introduced to further
assumptions (about handling the infinite, and various other issues),
equally reasonable and useful, and in accord both with our everyday
intuitions (insofar as they are relevant) and with the rest of
mainstream mathematics. And on the basis of those assumptions,
you can prove that
1 + 2 + 3 + … = –1/12.
That’s right, the sum of all the natural numbers equals –1/12.
This result is so much in-your-face, that people whose mathematics
education stopped at the undergraduate level (if they got that far)
typically say it is wrong. It’s not. Just as with the 0.999… example,
where we had to construct a proper meaning for an infinite decimal
expansion before we could determine what its value is, so to we
have to define what that infinite sum means. ….”
For a correction to Devlin’s remarks, see a physics professor’s weblog post —
“From a strictly mathematical point of view,
the equation 1+2+3+4+ … = -1/12 is incorrect,
and involves confusing the Dirichlet series with
the zeta function.” — Greg Gbur, May 25, 2010
From an obituary for a Kennedy advisor
who reportedly died at 94 on February 23, 2014*—
“He favored withdrawing rural civilians
into what he called ‘strategic hamlets’
and spraying defoliants to cut off
the enemy’s food supply.”
Other rhetoric: Hamlet and Infinite Space in this journal,
as well as King of Infinite Space , Part I and Part II.
These “King” links, to remarks on Coxeter and Saniga ,
are about two human beings to whom Hamlet’s
phrase “king of infinite space” has been applied.
The phrase would, of course, be more accurately
applied to God.
* The date of the ‘God’s Architecture’ sermon
at Princeton discussed in this afternoon’s post.
Edward Frenkel on Eichler's reciprocity law
(Love and Math , Kindle edition of 2013-10-01,
page 88, location 1812)—
"It seems nearly unbelievable that there
would be a rule generating these numbers.
And yet, German mathematician Martin
Eichler discovered one in 1954.11 "
"11. I follow the presentation of this result
given in Richard Taylor, Modular arithmetic:
driven by inherent beauty and human
curiosity , The Letter of the Institute for
Advanced Study [IAS], Summer 2012,
pp. 6– 8. I thank Ken Ribet for useful
comments. According to André Weil’s book
Dirichlet Series and Automorphic Forms ,
Springer-Verlag, 1971 [pp. 143-144], the
cubic equation we are discussing in this
chapter was introduced by John Tate,
following Robert Fricke."
|
Update of Feb. 19:
Actually, the cubic equation discussed Y 2 + Y = X 3 – X 2
whereas the equation given by Weil, Y 2 – Y = X 3 – X 2 .
Whether this is a misprint in Weil's book,
At any rate, the cubic equation discussed by
For further background, see (for instance) |
Richard Taylor, op. cit. —
|
One could ask for a similar method that given any number of polynomials in any number of variables helps one to determine the number of solutions to those equations in arithmetic modulo a variable prime number p . Such results are referred to as “reciprocity laws.” In the 1920s, Emil Artin gave what was then thought to be the most general reciprocity law possible—his abelian reciprocity law. However, Artin’s reciprocity still only applied to very special equations—equations with only one variable that have “abelian Galois group.” Stunningly, in 1954, Martin Eichler (former IAS Member) found a totally new reciprocity law, not included in Artin’s theorem. (Such reciprocity laws are often referred to as non-abelian.) More specifically, he found a reciprocality [sic ] law for the two variable equation Y 2 + Y = X 3 – X 2. He showed that the number of solutions to this equation in arithmetic modulo a prime number p differs from p [in the negative direction] by the coefficient of q p in the formal (infinite) product
q (1 – q 2 )(1 – q 11) 2 (1 – q 2)2 For example, you see that the coefficient of q5 is 1, so Eichler’s theorem tells us that Y 2 + Y = X 3 − X 2 should have 5 − 1 = 4 solutions in arithmetic modulo 5. You can check this by checking the twenty-five possibilities for (X,Y) modulo 5, and indeed you will find exactly four solutions: (X,Y) ≡ (0,0), (0,4), (1,0), (1,4) mod 5. Within less than three years, Yutaka Taniyama and Goro Shimura (former IAS Member) proposed a daring generalization of Eichler’s reciprocity law to all cubic equations in two variables. A decade later, André Weil (former IAS Professor) added precision to this conjecture, and found strong heuristic evidence supporting the Shimura-Taniyama reciprocity law. This conjecture completely changed the development of number theory. |
With this account and its context, Taylor has
perhaps atoned for his ridiculous remarks
quoted at Log24 in The Proof and the Lie.
Review —
From a Jan. 20, 2011, Emory University press release —
"Finite formula found for partition numbers" —
"We found a function, that we call P, that is like
a magical oracle," Ono says. "I can take any number,
plug it into P, and instantly calculate the partitions
of that number. P does not return gruesome numbers
with infinitely many decimal places. It's the finite,
algebraic formula that we have all been looking for."
Some may prefer Chinese oracles.
The title refers to a classic 1960 novel by John Hersey.
“How do you get young people excited about space?”
— Megan Garber in The Atlantic , Aug. 16, 2012
(Italics added.) (See previous four posts.)
Allyn Jackson on “Simplicity, in Mathematics and in Art,”
in the new August 2013 issue of Notices of the American
Mathematical Society—
“As conventions evolve, so do notions of simplicity.
Franks mentioned Gauss’s 1831 paper that
established the respectability of complex numbers.”
This suggests a related image by Gauss, with a
remark on simplicity—
Here Gauss’s diagram is not, as may appear at first glance,
a 3×3 array of squares, but is rather a 4×4 array of discrete
points (part of an infinite plane array).
Related material that does feature the somewhat simpler 3×3 array
of squares, not seen as part of an infinite array—
Marketing the Holy Field
Click image for the original post.
For a purely mathematical view of the holy field, see Visualizing GL(2,p).
The New York Times philosophy column "The Stone"
last evening had an essay on art by a sarcastic anarchist,
one Crispin Sartwell—
"… whole generations of art lovers have been
trained in modernist dogma, and arts institutions’
access to various forms of state or foundation
support depend on it completely. One goes to
the museum to gasp at stunning works of
incomparable, super-human genius by beings
who are infinitely more exalted and important
than the mere humans staring at their paintings.
That’s why ordinary people staring at a Picasso
(allegedly) experience a kind of transcendence
or re-articulation of their lives and world."
Cubism Re-Articulated:
Click image for some backstory.
(IMAGE: Walter Gropius and Froebel's Third Gift,
from a Google image search today)
Background: Cubism in this journal and
Pilate Goes to Kindergarten.
Related material: Chesterton + Thursday in this journal.
See Coxeter + Aleph in this journal.
Epigraph to "The Aleph," a 1945 story by Borges:
"O God! I could be bounded in a nutshell,
and count myself a King of infinite space…"
– Hamlet, II, 2
Rachel Dodes in The Wall Street Journal
on All Souls' Day, 2012—
"In one of the first lines uttered by Daniel Day-Lewis, playing Abraham Lincoln in the new Steven Spielberg film opening Nov. 9, he says, 'I could be bounded in a nutshell, and count myself a king of infinite space— were it not that I have bad dreams.'
The line was ripped straight from 'Hamlet,' by Lincoln's favorite writer, William Shakespeare. Tony Kushner, the Pulitzer Prize-winning playwright ('Angels in America') who wrote the script for the film, says that Shakespeare, much like Lincoln, 'had extraordinary mastery over the darkest parts of the human spirit.'"
The above quotation omits Shakespeare's words prefacing the nutshell part— "O God."
These same words in a different tongue— "Hey Ram"— have often been quoted as the last words of Gandhi. (See yesterday's noon post.)
"… for the Highest Essence (brahman ),
which is the core of the world, is identical
with the Highest Self (ātman ), the kernel
of man's existence."
— Heinrich Zimmer, Myths and Symbols
in Indian Art and Civilization , Pantheon
Books, 1946, page 142
Related material: A post linked to here on Friday night
that itself links to a different Shakespeare speech.
The title refers to a search (see below)
suggested by three things—
The search— Labyrinth 23.
(Within the search results, note particularly the post "The Infinity Point.")
"The word 'space' has, as you suggest, a large number of different meanings."
— Nanavira Thera in [Early Letters. 136] 10.xii.1958
From that same letter (links added to relevant Wikipedia articles)—
|
Space (ākāsa) is undoubtedly used in the Suttas
Your second letter seems to suggest that the space |
A simpler metaphysical system along the same lines—
|
The theory, he had explained, was that the persona
— The Gameplayers of Zan , |
"I am glad you have discovered that the situation is comical:
ever since studying Kummer I have been, with some difficulty,
refraining from making that remark."
— Nanavira Thera, [Early Letters, 131] 17.vii.1958
For those who prefer fiction:
"Many Dimensions (1931) — An evil antiquarian illegally purchases
the fabled Stone of Suleiman (Williams uses this Muslim form
rather than the more familiar King Solomon) from its Islamic guardian
in Baghdad and returns to England to discover not only that the Stone
can multiply itself infinitely without diminishing the original, but that it
also allows its possessor to transcend the barriers of space and time."
— Wikipedia article on the author Charles Williams
Jim Holt in tomorrow’s New York Times—
“Allow me to quote Nietzsche
(although I know that will be considered
by some to be in bad taste):
‘As the circle of science grows larger,
it touches paradox at more places.'”
A possible source for this misquotation—
Harvard University Press—
A more accurate quotation—
Anyone who has ever experienced the pleasure of Socratic insight and felt how, spreading in ever-widening circles, it seeks to embrace the whole world of appearances, will never again find any stimulus toward existence more violent than the craving to complete this conquest and to weave the net impenetrably tight. To one who feels that way, the Platonic Socrates will appear as the teacher of an altogether new form of “Greek cheerfulness” and blissful affirmation of existence that seeks to discharge itself in actions— most often in maieutic and educational influences on noble youths, with a view to eventually producing a genius.
But science, spurred by its powerful illusion, speeds irresistibly towards its limits where its optimism, concealed in the essence of logic, suffers shipwreck. For the periphery of the circle of science has an infinite number of points; and while there is no telling how this circle could ever be surveyed completely, noble and gifted men nevertheless reach, e’er half their time and inevitably, such boundary points on the periphery from which one gazes into what defies illumination. When they see to their horror how logic coils up at these boundaries and finally bites its own tail— suddenly the new form of insight breaks through, tragic insight which, merely to be endured, needs art as a protection and remedy.
— Friedrich Nietzsche, The Birth of Tragedy , translated by Walter Kaufmann (Modern Library)

Jamie James in The Music of the Spheres
(Springer paperback, 1995), page 28—
Pythagoras constructed a table of opposites
from which he was able to derive every concept
needed for a philosophy of the phenomenal world.
As reconstructed by Aristotle in his Metaphysics,
the table contains ten dualities….
|
Limited |
Unlimited |
Of these dualities, the first is the most important;
all the others may be seen as different aspects
of this fundamental dichotomy.
For further information, search on peiron + apeiron or
consult, say, Ancient Greek Philosophy , by Vijay Tankha.
The limited-unlimited contrast is not unrelated to the
contrasts between
From a film released Friday, April 13th, 2012—

"Time for you to see the field." — Bagger Vance, as quoted here yesterday.
* Title courtesy of David Foster Wallace.
(Continued from March 10, 2012)
An inaccuracy in a passage linked to yesterday—
“The created universe, the whole of things, is,
in words from Joyce’s Ulysses , ‘predicated on the void.'”
The “predicated” phrase seems to be absent from Ulysses .
Joyce does, however, have the following (from ricorso.net)—
| “William Blake” (March 1912) – cont.: ‘Armed with this two-edged sword, the art of Michaelangelo and the revelations of Swedenborg, Blake killed the dragon of experience and natural wisdom, and, by minimising space and time and denying the existence of memory and the senses, he tried to paint his works on the void of the divine bosom. [See note, infra.]To him, each moment shorter than a pulse-beat was equivalent in its duration to six thousand years, because in such an infinitely short instant the work of the poet is conceived and born. To him, all space larger than a red globule of human blood was visionary, created by the hammer of Los, while in a space smaller than a globule of blood we approach eternity, of which our vegetable world is but a shadow. Not with the eye, then, but beyond the eye, the soul and the supreme move must look, because the eye, which was born in the night while the soul was sleeping in rays of light, will also die in the night. […] The mental process by which Blake arrives at the threshold of the infinite is a similar process. Flying from the infinitely small to the infinitely large, from a drop of blood to the universe of stars, his soul is consumed by the rapidity of flight, and finds itself renewed and winged and immortal on the edge of th dark ocean of God. And althought he based his art on such idealist premises, convinced that eternity was in love with the products of time, this sons of God with the sons of [MS ends here].’ (Critical Writings, 1959, 1966 Edn., pp.221-22; quoted [in part] in Richard Ellmann, James Joyce, 1965 Edn., p.330.) [For full text, see RICORSO Library, “Major Authors”, via index, or direct.] Note – for “void” [supra] , cf. Stephen in “Scylla & Charybdis”: ‘Fatherhood […] is a mystical estate, an apostolic succession, from only begetter to only begotten. On that mystery and not on the madonna which the cunning Italian intellect flung to the mob of Europe the church is founded and founded irremovably because founded, like the world, macro- and microcosm, upon the void.’ (Ulysses, Penguin Edn. 1967, p.207; [my itals.].) |
Some academics may prefer a more leftist version of
“predicated on the void”—

Post 2310 in yesterday evening’s Short Story links to two posts
from 2006 inspired by Oxford mathematician Marcus du Sautoy—
|
Thursday, May 25, 2006
|
The first paragraph of
“Zeta Functions of Groups: The Quest for Order
Versus the Flight from Ennui,” by Marcus du Sautoy,
Mathematical Institute, University of Oxford—
“Mathematics is about the search for patterns,
to see order where others see chaos. We are very lucky
to find ourselves studying a subject which is neither so rigid
that the patterns are easy, yet not too complicated
lest our brains fail to master its complexities.
John Cawelti sums up this interplay perfectly in a book*
not about mathematics but about mystery and romance:
‘if we seek order and security, the result is likely to be
boredom and sameness. But rejecting order for the sake
of change and novelty brings danger and uncertainty…
the history of culture can be interpreted as a dynamic
tension between these two basic impulses…
between the quest for order and the flight from ennui.”’
* John G. Cawelti, Adventure, Mystery, and Romance:
Formula Stories as Art and Popular Culture ,
University of Chicago Press, 1976.
[Cawelti cites as his souce on interpreting “the history
of culture” Harry Berger, Jr., “Naive Consciousness and
Culture Change: An Essay in Historical Structuralism,”
Bulletin of the Midwest Modern Language Association ,
Vol. 6, No. 1 (Spring 1973): page 35.]
Here du Sautoy paints mathematicians as seekers of order,
apparently not realizing that the author he approvingly quotes
states that seekers of order face the danger of boredom.
Another danger to seekers
of order is, of course, seeing
order where there is none.
The reported last words of
Apple founder Steve Jobs were
"Oh wow. Oh wow. Oh wow."
In the spirit of these words, a
Google search from today—
See also…
Peter J. Cameron yesterday on Galois—
"He was killed in a duel at the age of 20…. His work languished for another 14 years until Liouville published it in his Journal; soon it was recognised as the foundation stone of modern algebra, a position it has never lost."
Here Cameron is discussing Galois theory, a part of algebra. Galois is known also as the founder* of group theory, a more general subject.
Group theory is an essential part of modern geometry as well as of modern algebra—
"In der Galois'schen Theorie, wie hier, concentrirt sich das Interesse auf Gruppen von Änderungen. Die Objecte, auf welche sich die Änderungen beziehen, sind allerdings verschieden; man hat es dort mit einer endlichen Zahl discreter Elemente, hier mit der unendlichen Zahl von Elementen einer stetigen Mannigfaltigkeit zu thun."
— Felix Christian Klein, Erlanger Programm , 1872
("In the Galois theory, as in ours, the interest centres on groups of transformations. The objects to which the transformations are applied are indeed different; there we have to do with a finite number of discrete elements, here with the infinite number of elements in a continuous manifoldness." (Translated by M.W. Haskell, published in Bull. New York Math. Soc. 2, (1892-1893), 215-249))
Related material from Hermann Weyl, Symmetry , Princeton University Press, 1952 (paperback reprint of 1982, pp. 143-144)—
"A field is perhaps the simplest algebraic structure we can invent. Its elements are numbers…. Space is another example of an entity endowed with a structure. Here the elements are points…. What we learn from our whole discussion and what has indeed become a guiding principle in modern mathematics is this lesson: Whenever you have to do with a structure-endowed entity Σ try to determine is group of automorphisms , the group of those element-wise transformations which leave all structural relations undisturbed. You can expect to gain a deep insight into the constitution of Σ in this way."
For a simple example of a group acting on a field (of 8 elements) that is also a space (of 8 points), see Generating the Octad Generator and Knight Moves.
* Joseph J. Rotman, An Introduction to the Theory of Groups , 4th ed., Springer, 1994, page 2
Review of DeLillo's novel Point Omega—
"One difference between art and entertainment has to do with the speed of perception. Art deliberately slows and complicates reading, hearing, and/or viewing so that you’re challenged to re-think and re-feel form and experience. Entertainment deliberately accelerates and simplifies them so that you don’t have to think about or feel very much of anything at all except, perhaps, the adrenalin rush before dazzling spectacle. Although, of course, there can be myriad gradations between the former and latter, in their starkest articulation we’re talking about the distance between, say, David Foster Wallace’s Infinite Jest and Dan Brown’s The Lost Symbol…."
— Lance Olsen, March 1, 2010, in The Quarterly Conversation
Robert Hughes on fast and slow art—
"We have had a gutful of fast art and fast food. What we need more of is slow art: art that holds time as a vase holds water: art that grows out of modes of perception and whose skill and doggedness make you think and feel; art that isn't merely sensational, that doesn't get its message across in 10 seconds, that isn't falsely iconic, that hooks onto something deep-running in our natures. In a word, art that is the very opposite of mass media. For no spiritually authentic art can beat mass media at their own game."
– Speech of June 1, 2004
Log24 on art speeds—
A Study in Art Education (June 15, 2007)
Twenty-four (March 13, 2011)
Ben Brantley in The New York Times on May 26—
While you theatergoing butterflies out there keep nattering on about the Tonys— who will win, who should win, and so on— I have been focused on an issue of far greater momentousness and urgency. That’s the shameful squandering on Broadway of what our country would seem to believe is our most valued (and infinitely exploitable) natural resource: our celebrities….
Lindsay Lohan: This undeniably talented (and for all intents and purposes, former) film actress poses a special challenge. Her only recent work appears to have been as a paparazzi model and professional partygoer, and a big, line-laden dramatic part like Blanche DuBois might be too onerous to start with. So why not put her in the Broadway premiere of “Finishing the Picture,” a late-career Arthur Miller play inspired by the travails of making a movie (“The Misfits”) with his wife Marilyn Monroe? Having seen a production of this play in Chicago, I can testify that the Marilyn part requires only that the actress playing her be willing to appear asleep and stupefied and, briefly, to walk across the stage naked. For Ms. Lohan, who credibly impersonated Marilyn for a New York magazine photo shoot, this ought to be a cinch. Should an eight-performance week prove too taxing, I suggest Paris Hilton for matinees.
This midnight post was suggested by Sunday's midday 4-digit NY Lottery number, 7286, and by the following web pages:
7286 Style by Lindsay Lohan and 7286 Prisoner Transport.
Some background from a third 7286 web page—
Starlet Lindsay Lohan is bringing her signature Hollywood style to the masses with her new 7286 line. The starlet's stylish stamp is on every aspect of the line, from the name (7-2-86 is her birthday) to the brand's tag line : "Give a girl the right handbag, and she can conquer the world!"
A Meditation on the NY Lottery of May 29
Yesterday's NY Lottery— Midday 981, Evening 275.
As noted in yesterday morning's linked-to post,
The Shining of May 29…
"By groping toward the light we are made to realize
how deep the darkness is around us."
— Arthur Koestler, The Call Girls: A Tragi-Comedy ,
Random House, 1973, page 118
One interpretation of the mystic numbers revealed by the Lottery yesterday—
981 as the final page* of David Foster Wallace's famed novel Infinite Jest …

275 as a page in Wallace's non-fiction book about infinity Everything and More …

Gregory Chaitin points out that this is nonsense …

As noted elsewhere in this journal, I have a different concept of "math's absolute
Prince of Darkness"— and, indeed, of a "quest for Omega." (See posts of May 2010.)
Yesterday's numbers indicate a different struggle between darkness and light—
Light —

Darkness —

* From infinitesummer.org/archives/168 — "A note about editions:
As it turns out, all (physical) editions of Infinite Jest have 981 pages:
the one from 1996, the one from 2004, the paperback, the hardcover, etc.
A big thank you to the men and women in the publishing industry who
were kind and/or lazy enough to keep things consistent."
Heisenberg on Heraclitus
From Physics and Philosophy , by Werner Heisenberg, 1958, reprinted by Penguin Classics, 2003—
Page 28—
… In the philosophy of Heraclitus of Ephesus the concept of Becoming occupies the foremost
place. He regarded that which moves, the fire, as the basic element. The difficulty, to reconcile
the idea of one fundamental principle with the infinite variety of phenomena, is solved for him by
recognizing that the strife of the opposites is really a kind of harmony. For Heraclitus the world is
at once one and many, it is just 'the opposite tension' of the opposites that constitutes the unity
of the One. He says: 'We must know that war is common to all and strife is justice, and that all
things come into being and pass away through strife.'
Looking back to the development of Greek philosophy up to this point one realizes that it has
been borne from the beginning to this
Page 29—
stage by the tension between the One and the Many. For our senses the world consists of an
infinite variety of things and events, colors and sounds. But in order to understand it we have to
introduce some kind of order, and order means to recognize what is equal, it means some sort
of unity. From this springs the belief that there is one fundamental principle, and at the same
time the difficulty to derive from it the infinite variety of things. That there should be a material
cause for all things was a natural starting point since the world consists of matter. But when one
carried the idea of fundamental unity to the extreme one came to that infinite and eternal
undifferentiated Being which, whether material or not, cannot in itself explain the infinite variety
of things. This leads to the antithesis of Being and Becoming and finally to the solution of
Heraclitus, that the change itself is the fundamental principle; the 'imperishable change, that
renovates the world,' as the poets have called it. But the change in itself is not a material cause
and therefore is represented in the philosophy of Heraclitus by the fire as the basic element,
which is both matter and a moving force.
We may remark at this point that modern physics is in some way extremely near to the
doctrines of Heraclitus. If we replace the word 'fire' by the word 'energy' we can almost repeat
his statements word for word from our modern point of view. Energy is in fact the substance
from which all elementary particles, all atoms and therefore all things are made, and energy is
that which moves. Energy is a substance, since its total amount does not change, and the
elementary particles can actually be made from this substance as is seen in many experiments on
the creation of elementary particles. Energy can be changed into motion, into heat, into light
and into tension. Energy may be called the fundamental cause for all change in the world. But this
comparison of Greek philosophy with the ideas of modern science will be discussed later.
* See earlier uses of the phrase in this journal. Further background— Hopkins and Heraclitus.
Literary remarks for Maundy Thursday—

— C. P. Snow, foreword to G. H. Hardy's A Mathematician's Apology
Related material—
Emory University press release of January 20th, 2011:
"In 1937, Hans Rademacher found an exact formula for calculating partition values. While the method was a big improvement over Euler's exact formula, it required adding together infinitely many numbers that have infinitely many decimal places. 'These numbers are gruesome,' Ono says….
… The final eureka moment occurred near another Georgia landmark: Spaghetti Junction. Ono and Jan Bruinier were stuck in traffic near the notorious Atlanta interchange. While chatting in the car, they hit upon a way to overcome the infinite complexity of Rademacher's method. They went on to prove a formula that requires only finitely many simple numbers.
'We found a function, that we call P, that is like a magical oracle,' Ono says. 'I can take any number, plug it into P, and instantly calculate the partitions of that number….'"
See also this journal on April 15 and a Google Groups [sage-devel] thread, Ono-Bruinier partition formula. That thread started on April 15 and was last updated this morning.
Conclusion of “The Place of Pure Mathematics” —
“Dogmas and philosophies, it would seem, rise and fall. But gradually accumulating throughout the ages, from the earliest dawn of history, there is a body of doctrine, a reasoned insight into the relations of exact ideas, painfully won and often tested. And this remains the main heritage of man; his little beacon of light amidst the solitudes and darknesses of infinite space; or, if you prefer, like the shout of children at play together in the cultivated valleys, which continues from generation to generation.
Yes, and continues for ever! A universe which has the potentiality of becoming thus conscious of itself is not without something of which that which we call memory is but an image. Somewhere, somehow, in ways we dream not of, when you and I have merged again into the illimitable whole, when all that is material has ceased, the faculty in which we now have some share, shall surely endure; the conceptions we now dimly struggle to grasp, the joy we have in the effort, these are but part of a greater whole. Some may fear, and some may hope, that they and theirs shall not endure for ever. But he must have studied Nature in vain who does not see that our spiritual activities are inherent in the mighty process of which we are part; who can doubt of their persistence.
And, on the intellectual side, of all that is best ascertained, and surest, and most definite, of these; of all that is oldest and most universal; of all that is most fundamental and far-reaching, of these activities, Pure Mathematics is the symbol and the sum.”
— From a 1913 address by geometry saint Henry Frederick Baker, who died on this date in 1956
The feast of another saint, Patrick, also falls on 3/17. The date itself is related, if only by chance, to the following remark—
“317 is a prime, not because we think so,
or because our minds are shaped in one way
rather than another, but because it is so,
because mathematical reality is built that way.”
— From a 1940 book by the somewhat less saintly number theorist G. H. Hardy
Indiana Jones and the Magical Oracle
Mathematician Ken Ono in the December 2010 American Mathematical Society Notices—

The "dying genius" here is Ramanujan, not Galois. The story now continues at the AMS website—

(Excerpt from Jan. 27 screenshot;
the partitions story has been the top
news item at the site all week.)
From a Jan. 20, 2011, Emory University press release —
"Finite formula found for partition numbers" —
"We found a function, that we call P, that is like a magical oracle," Ono says. "I can take any number, plug it into P, and instantly calculate the partitions of that number. P does not return gruesome numbers with infinitely many decimal places. It's the finite, algebraic formula that we have all been looking for."
For an introduction to the magical oracle, see a preprint, "Bruinier-Ono," at the American Institute of Mathematics website.
Ono also discussed the oracle in a video (see minute 25) recorded Jan. 21 and placed online today.
See as well "Exact formulas for the partition function?" at mathoverflow.net.
A Nov. 29, 2010, remark by Thomas Bloom on that page leads to a 2006 preprint by Ono and Kathrin Bringmann, "An Arithmetic Formula for the Partition Function*," that seems not unrelated to Ono's new "magical oracle" formula—
The Bruinier-Ono paper does not mention the earlier Bringmann-Ono work.
(Both the 2011 Bruinier-Ono paper and the 2006 Bringmann-Ono paper mention their debt to a 2002 work by Zagier— Don Zagier, "Traces of singular moduli," in Motives, Polylogarithms and Hodge theory, Part II (Irvine, CA, 1998), International Press Lecture Series 3 (International Press, Somerville, MA, 2002), pages 211-244.)
Some background for those who prefer mathematics to narrative—
The Web of Modularity: Arithmetic of the Coefficients of Modular Forms and q-Series ,
by Ken Ono, American Mathematical Society CBMS Series, 2004.
Where Entertainment Is God continues...
New York Lottery today— Midday 710, Evening 563.
This suggeests a scientific note from the date 7/10 (2009) and the page number 563 from Dec. 29—
Bulletin of the American Mathematical Society , October 2002, p. 563:
“To produce decorations for their weaving, pottery, and other objects, early artists experimented with symmetries and repeating patterns. Later the study of symmetries of patterns led to tilings, group theory, crystallography, finite geometries, and in modern times to security codes and digital picture compactifications. Early artists also explored various methods of representing existing objects and living things. These explorations led to… [among other things] computer-generated movies (for example, Toy Story ).”
– David W. Henderson, Cornell University
For a different perspective on Toy Story , see the Dec. 29 post.
Other entertainments — The novel Infinite Jest and two versions of "Heeere's Johnny !" —
From Stanley Kubrick and from today's New York Times :

See also All Things Shining and the lottery theology of Jorge Luis Borges.
(A continuation of this morning's Coxeter and the Aleph)
"You've got to pick up every stitch… Must be the season of the witch."
— Donovan song at the end of Nicole Kidman's "To Die For"
| Mathematics and Narrative, Illustrated | |

|
 Narrative |
"As is well known, the Aleph is the first letter of the Hebrew alphabet.
Its use for the strange sphere in my story may not be accidental.
For the Kabbala, the letter stands for the En Soph ,
the pure and boundless godhead; it is also said that it takes
the shape of a man pointing to both heaven and earth, in order to show
that the lower world is the map and mirror of the higher; for Cantor's
Mengenlehre , it is the symbol of transfinite numbers,
of which any part is as great as the whole."
— Borges, "The Aleph"
From WorldLingo.com —
|
"Infinite Jest… now stands as the principal contender
for what serious literature can aspire to
in the late twentieth and early twenty-first centuries."
— All Things Shining, a work of pop philosophy published January 4th
"You're gonna need a bigger boat." — Roy Scheider in "Jaws"
"We're gonna need more holy water." — "Season of the Witch," a film opening tonight
See also, with respect to David Foster Wallace, infinity, nihilism,
and the above reading of "Ayn Sof" as "nothingness,"
the quotations compiled as "Is Nothing Sacred?"
In a nutshell —
Epigraph to "The Aleph," a 1945 story by Borges:
O God! I could be bounded in a nutshell,
and count myself a King of infinite space…
— Hamlet, II, 2

The story in book form, 1949
A 2006 biography of geometer H.S.M. Coxeter:

The Aleph (implicit in a 1950 article by Coxeter):

The details:
Related material: Group Actions, 1984-2009.
In memory of kaleidoscope enthusiast Cozy Baker, who died at 86, according to Saturday's Washington Post , on October 19th.
This journal on that date — Savage Logic and Savage Logic continued.
See this journal on All Saints' Day 2006 for some background to those posts—
“Savage logic works like a kaleidoscope whose chips can fall into a variety of patterns while remaining unchanged in quantity, form, or color. The number of patterns producible in this way may be large if the chips are numerous and varied enough, but it is not infinite. The patterns consist in the disposition of the chips vis-a-vis one another (that is, they are a function of the relationships among the chips rather than their individual properties considered separately). And their range of possible transformations is strictly determined by the construction of the kaleidoscope, the inner law which governs its operation. And so it is too with savage thought. Both anecdotal and geometric, it builds coherent structures out of ‘the odds and ends left over from psychological or historical process.’
These odds and ends, the chips of the kaleidoscope, are images drawn from myth, ritual, magic, and empirical lore. (How, precisely, they have come into being in the first place is one of the points on which Levi-Strauss is not too explicit, referring to them vaguely as the ‘residue of events… fossil remains of the history of an individual or a society.’) Such images are inevitably embodied in larger structures– in myths, ceremonies, folk taxonomies, and so on– for, as in a kaleidoscope, one always sees the chips distributed in some pattern, however ill-formed or irregular. But, as in a kaleidoscope, they are detachable from these structures and arrangeable into different ones of a similar sort. Quoting Franz Boas that ‘it would seem that mythological worlds have been built up, only to be shattered again, and that new worlds were built from the fragments,’ Levi-Strauss generalizes this permutational view of thinking to savage thought in general.”
– Clifford Geertz, “The Cerebral Savage: the Structural Anthropology of Claude Levi-Strauss,” in Encounter, Vol. 28 No. 4 (April 1967), pp. 25-32.
Related material —
See also "Levi-Strauss" in this journal and "At Play in the Field."
Thanks to David Lavery for the following dialogue on the word "narrative" in politics—
"It's like – does this fit into narrative?
It's like, wait, wait, what about a platform? What about, like, ideas?
What about, you know, these truths we hold to be self-evident?
No, it's the narrative."
"Is narrative a fancy word for spin?"
Related material —
Church Logic (Log24, October 29) —
What sort of geometry
is the following?
"What about, you know, these truths we hold to be self-evident?"
Some background from Cambridge University Press in 1976 —

Commentary —
The Church Logic post argues that Cameron's implicit definition of "non-Euclidean" is incorrect.
The four-point, six-line geometry has as lines "all subsets of the point set" which have cardinality 2.
It clearly satisfies Euclid's parallel postulate. Is it, then, not non-Euclidean?
That would, according to the principle of the excluded middle (cf. Church), make it Euclidean.
A definition from Wikipedia that is still essentially the same as it was when written on July 14, 2003—
"Finite geometry describes any geometric system that has only a finite number of points. Euclidean geometry, for example, is not finite, because a Euclidean line contains infinitely many points…."
This definition would seem to imply that a finite geometry (such as the four-point geometry above) should be called non -Euclidean whether or not it violates Euclid's parallel postulate. (The definition's author, unlike many at Wikipedia, is not anonymous.)
See also the rest of Little Gidding.
Barnes & Noble has an informative new review today of the recent Galois book Duel at Dawn.
It begins…
"In 1820, the Hungarian noble Farkas Bolyai wrote an impassioned cautionary letter to his son Janos:
'I know this way to the very end. I have traversed this bottomless night, which extinguished all light and joy in my life… It can deprive you of your leisure, your health, your peace of mind, and your entire happiness… I turned back when I saw that no man can reach the bottom of this night. I turned back unconsoled, pitying myself and all mankind. Learn from my example…'
Bolyai wasn't warning his son off gambling, or poetry, or a poorly chosen love affair. He was trying to keep him away from non-Euclidean geometry."
For a less dark view (obtained by simply redefining "non-Euclidean" in a more logical way*) see Non-Euclidean Blocks and Finite Geometry and Physical Space.
* Finite geometry is not Euclidean geometry— and is, therefore, non-Euclidean
in the strictest sense (though not according to popular usage), simply because
Euclidean geometry has infinitely many points, and a finite geometry does not.
(This more logical definition of "non-Euclidean" seems to be shared by
at least one other person.)
And some finite geometries are non-Euclidean in the popular-usage sense,
related to Euclid's parallel postulate.
The seven-point Fano plane has, for instance, been called
"a non-Euclidean geometry" not because it is finite
(though that reason would suffice), but because it has no parallel lines.
(See the finite geometry page at the Centre for the Mathematics
of Symmetry and Computation at the University of Western Australia.)
"Things fall apart;
the centre cannot hold"

The above building is home to the Derridean leftists
of the Villanova philosophy department.
“center loosens,
forms again elsewhere”
|
"The most obvious problem with Derrida's argument in The Gift of Death is his misconception of Christianity. In his description of Christian mystery, the crucified figure of Jesus is strikingly absent, having been replaced by a mysterious 'infinite other.' In this respect, Derrida's understanding of Christianity is essentially gnostic; the humanity of Jesus is displaced by gnostic mystery. Although Derrida claims to describe historical Christianity, in fact, his argument is based on a serious distortion of Christian practice and theology. Although the title might seem an obvious reference to Christ's atoning death, Derrida's book can only be characterized as an overt and unacknowledged displacement of the Crucifixion and its central place in Christian worship."
— Peter Goldman, now at Westminster College in Salt Lake City |
See also Highway 1 Revisited (August 1, 2006).
Excerpts from "The Concept of Group and the Theory of Perception,"
by Ernst Cassirer, Philosophy and Phenomenological Research,
Volume V, Number 1, September, 1944.
(Published in French in the Journal de Psychologie, 1938, pp. 368-414.)
The group-theoretical interpretation of the fundaments of geometry is,
from the standpoint of pure logic, of great importance, since it enables us to
state the problem of the "universality" of mathematical concepts in simple
and precise form and thus to disentangle it from the difficulties and ambigui-
ties with which it is beset in its usual formulation. Since the times of the
great controversies about the status of universals in the Middle Ages, logic
and psychology have always been troubled with these ambiguities….
Our foregoing reflections on the concept of group permit us to define more
precisely what is involved in, and meant by, that "rule" which renders both
geometrical and perceptual concepts universal. The rule may, in simple
and exact terms, be defined as that group of transformations with regard to
which the variation of the particular image is considered. We have seen
above that this conception operates as the constitutive principle in the con-
struction of the universe of mathematical concepts….
…Within Euclidean geometry,
a "triangle" is conceived of as a pure geometrical "essence," and this
essence is regarded as invariant with respect to that "principal group" of
spatial transformations to which Euclidean geometry refers, viz., displace-
ments, transformations by similarity. But it must always be possible to
exhibit any particular figure, chosen from this infinite class, as a concrete
and intuitively representable object. Greek mathematics could not
dispense with this requirement which is rooted in a fundamental principle
of Greek philosophy, the principle of the correlatedness of "logos" and
"eidos." It is, however, characteristic of the modern development of
mathematics, that this bond between "logos" and "eidos," which was indis-
soluble for Greek thought, has been loosened more and more, to be, in the
end, completely broken….
…This process has come to its logical
conclusion and systematic completion in the development of modern group-
theory. Geometrical figures are no longer regarded as fundamental, as
date of perception or immediate intuition. The "nature" or "essence" of a
figure is defined in terms of the operations which may be said to
generate the figure. The operations in question are, in turn, subject to
certain group conditions….
…What we
find in both cases are invariances with respect to variations undergone by
the primitive elements out of which a form is constructed. The peculiar
kind of "identity" that is attributed to apparently altogether heterogen-
eous figures in virtue of their being transformable into one another by means
of certain operations defining a group, is thus seen to exist also in the
domain of perception. This identity permits us not only to single out ele-
ments but also to grasp "structures" in perception. To the mathematical
concept of "transformability" there corresponds, in the domain of per-
ception, the concept of "transposability." The theory of the latter con-
cept has been worked out step by step and its development has gone through
various stages….
…By the acceptance of
"form" as a primitive concept, psychological theory has freed it from the
character of contingency which it possessed for its first founders. The inter-
pretation of perception as a mere mosaic of sensations, a "bundle" of simple
sense-impressions has proved untenable….
…In the domain of mathematics this state of affairs mani-
fests itself in the impossibility of searching for invariant properties of a
figure except with reference to a group. As long as there existed but one
form of geometry, i.e., as long as Euclidean geometry was considered as the
geometry kat' exochen this fact was somehow concealed. It was possible
to assume implicitly the principal group of spatial transformations that lies
at the basis of Euclidean geometry. With the advent of non-Euclidean
geometries, however, it became indispensable to have a complete and sys-
tematic survey of the different "geometries," i.e., the different theories of
invariancy that result from the choice of certain groups of transformation.
This is the task which F. Klein set to himself and which he brought to a
certain logical fulfillment in his Vergleichende Untersuchungen ueber neuere
geometrische Forschungen….
…Without discrimination between the
accidental and the substantial, the transitory and the permanent, there
would be no constitution of an objective reality.
This process, unceasingly operative in perception and, so to speak, ex-
pressing the inner dynamics of the latter, seems to have come to final per-
fection, when we go beyond perception to enter into the domain of pure
thought. For the logical advantage and peculiar privilege of the pure con –
cept seems to consist in the replacement of fluctuating perception by some-
thing precise and exactly determined. The pure concept does not lose
itself in the flux of appearances; it tends from "becoming" toward "being,"
from dynamics toward statics. In this achievement philosophers have
ever seen the genuine meaning and value of geometry. When Plato re-
gards geometry as the prerequisite to philosophical knowledge, it is because
geometry alone renders accessible the realm of things eternal; tou gar aei
ontos he geometrike gnosis estin. Can there be degrees or levels of objec-
tive knowledge in this realm of eternal being, or does not rather knowledge
attain here an absolute maximum? Ancient geometry cannot but answer
in the affirmative to this question. For ancient geometry, in the classical
form it received from Euclid, there was such a maximum, a non plus ultra.
But modern group theory thinking has brought about a remarkable change
In this matter. Group theory is far from challenging the truth of Euclidean
metrical geometry, but it does challenge its claim to definitiveness. Each
geometry is considered as a theory of invariants of a certain group; the
groups themselves may be classified in the order of increasing generality.
The "principal group" of transformations which underlies Euclidean geome-
try permits us to establish a number of properties that are invariant with
respect to the transformations in question. But when we pass from this
"principal group" to another, by including, for example, affinitive and pro-
jective transformations, all that we had established thus far and which,
from the point of view of Euclidean geometry, looked like a definitive result
and a consolidated achievement, becomes fluctuating again. With every
extension of the principal group, some of the properties that we had taken
for invariant are lost. We come to other properties that may be hierar-
chically arranged. Many differences that are considered as essential
within ordinary metrical geometry, may now prove "accidental." With
reference to the new group-principle they appear as "unessential" modifica-
tions….
… From the point of view of modern geometrical systematization,
geometrical judgments, however "true" in themselves, are nevertheless not
all of them equally "essential" and necessary. Modern geometry
endeavors to attain progressively to more and more fundamental strata of
spatial determination. The depth of these strata depends upon the com-
prehensiveness of the concept of group; it is proportional to the strictness of
the conditions that must be satisfied by the invariance that is a universal
postulate with respect to geometrical entities. Thus the objective truth
and structure of space cannot be apprehended at a single glance, but have to
be progressively discovered and established. If geometrical thought is to
achieve this discovery, the conceptual means that it employs must become
more and more universal….
In the above view, four of the tesseract's 16
vertices are overlaid by other vertices.
For views that are more complete and
moveable, see Smith's tesseract page.
Four-Part Tesseract Divisions—

The above figure shows how four-part partitions
of the 16 vertices of a tesseract in an infinite
Euclidean space are related to four-part partitions
of the 16 points in a finite Galois space
|
Euclidean spaces versus Galois spaces in a larger context—
Infinite versus Finite The central aim of Western religion —
"Each of us has something to offer the Creator...
the bridging of
masculine and feminine,
life and death.
It's redemption.... nothing else matters."
-- Martha Cooley in The Archivist (1998)
The central aim of Western philosophy —
Dualities of Pythagoras
as reconstructed by Aristotle:
Limited Unlimited
Odd Even
Male Female
Light Dark
Straight Curved
... and so on ....
"Of these dualities, the first is the most important; all the others may be seen as different aspects of this fundamental dichotomy. To establish a rational and consistent relationship between the limited [man, etc.] and the unlimited [the cosmos, etc.] is… the central aim of all Western philosophy." |
Another picture related to philosophy and religion—
Jung's Four-Diamond Figure from Aion—

This figure was devised by Jung
to represent the Self. Compare the
remarks of Paul Valéry on the Self—
|
Flight from Eden: The Origins of Modern Literary Criticism and Theory, by Steven Cassedy, U. of California Press, 1990, pages 156-157—
Valéry saw the mind as essentially a relational system whose operation he attempted to describe in the language of group mathematics. "Every act of understanding is based on a group," he says (C, 1:331). "My specialty— reducing everything to the study of a system closed on itself and finite" (C, 19: 645). The transformation model came into play, too. At each moment of mental life the mind is like a group, or relational system, but since mental life is continuous over time, one "group" undergoes a "transformation" and becomes a different group in the next moment. If the mind is constantly being transformed, how do we account for the continuity of the self? Simple; by invoking the notion of the invariant. And so we find passages like this one: "The S[elf] is invariant, origin, locus or field, it's a functional property of consciousness" (C, 15:170 [2:315]). Just as in transformational geometry, something remains fixed in all the projective transformations of the mind's momentary systems, and that something is the Self (le Moi, or just M, as Valéry notates it so that it will look like an algebraic variable). Transformation theory is all over the place. "Mathematical science… reduced to algebra, that is, to the analysis of the transformations of a purely differential being made up of homogeneous elements, is the most faithful document of the properties of grouping, disjunction, and variation in the mind" (O, 1:36). "Psychology is a theory of transformations, we just need to isolate the invariants and the groups" (C, 1:915). "Man is a system that transforms itself" (C, 2:896). O Paul Valéry, Oeuvres (Paris: Pléiade, 1957-60) C Valéry, Cahiers, 29 vols. (Paris: Centre National de le Recherche Scientifique, 1957-61) |
Note also the remarks of George David Birkhoff at Rice University
in 1940 (pdf) on Galois's theory of groups and the related
"theory of ambiguity" in Galois's testamentary letter—
|
… metaphysical reasoning always relies on the Principle of Sufficient Reason, and… the true meaning of this Principle is to be found in the “Theory of Ambiguity” and in the associated mathematical “Theory of Groups.” If I were a Leibnizian mystic, believing in his “preestablished harmony,” and the “best possible world” so satirized by Voltaire in “Candide,” I would say that the metaphysical importance of the Principle of Sufficient Reason and the cognate Theory of Groups arises from the fact that God thinks multi-dimensionally* whereas men can only think in linear syllogistic series, and the Theory of Groups is the appropriate instrument of thought to remedy our deficiency in this respect. * That is, uses multi-dimensional symbols beyond our grasp. |
Related material:
A medal designed by Leibniz to show how
binary arithmetic mirrors the creation by God
of something (1) from nothing (0).

Another array of 16 strings of 0's and 1's, this time
regarded as coordinates rather than binary numbers—


Some context by a British mathematician —

|
Imago by Wallace Stevens Who can pick up the weight of Britain, Who can move the German load Or say to the French here is France again? Imago. Imago. Imago. It is nothing, no great thing, nor man Of ten brilliancies of battered gold And fortunate stone. It moves its parade Of motions in the mind and heart, A gorgeous fortitude. Medium man In February hears the imagination's hymns And sees its images, its motions And multitudes of motions And feels the imagination's mercies, In a season more than sun and south wind, Something returning from a deeper quarter, A glacier running through delirium, Making this heavy rock a place, Which is not of our lives composed . . . Lightly and lightly, O my land, Move lightly through the air again. |
Continued from May 8
(Feast of Saint Robert Heinlein)
“Wells and trees were dedicated to saints. But the offerings at many wells and trees were to something other than the saint; had it not been so they would not have been, as we find they often were, forbidden. Within this double and intertwined life existed those other capacities, of which we know more now, but of which we still know little– clairvoyance, clairaudience, foresight, telepathy.”
— Charles Williams, Witchcraft, Faber and Faber, London, 1941
Why "Saint" Robert? See his accurate depiction of evil– the Eater of Souls in Glory Road.
For more on Williams's "other capacities," see Heinlein's story "Lost Legacy."
A related story– Fritz Leiber's "The Mind Spider." An excerpt:
The conference—it was much more a hyper-intimate
gabfest—proceeded.
"My static box bugged out for a few ticks this morning,"
Evelyn remarked in the course of talking over the
trivia of the past twenty-four hours.
The static boxes were an invention of Grandfather
Horn. They generated a tiny cloud of meaningless brain
waves. Without such individual thought-screens, there was
too much danger of complete loss of individual personality
—once Grandfather Horn had "become" his infant daughter
as well as himself for several hours and the unfledged
mind had come close to being permanently lost in its own
subconscious. The static boxes provided a mental wall be-
– hind which a mind could safely grow and function, similar
to the wall by which ordinary minds are apparently
always enclosed.
In spite of the boxes, the Horns shared thoughts and
emotions to an amazing degree. Their mental togetherness
was as real and as mysterious—and as incredible—as
thought itself . . . and thought is the original angel-cloud
dancing on the head of a pin. Their present conference
was as warm and intimate and tart as any actual family
gathering in one actual room around one actual table.
Five minds, joined together in the vast mental darkness
that shrouds all minds. Five minds hugged together for
comfort and safety in the infinite mental loneliness that
pervades the cosmos.
Evelyn continued, "Your boxes were all working, of
course, so I couldn't get your thoughts—just the blurs of
your boxes like little old dark grey stars. But this time
if gave me a funny uncomfortable feeling, like a spider
Crawling down my—Grayl! Don't feel so wildly! What
Is it?”
Then… just as Grayl started to think her answer…
something crept from the vast mental darkness and infinite
cosmic loneliness surrounding the five minds of the
Horns.
Grayl was the first to notice. Her panicky thought had
ttie curling too-keen edge of hysteria. "There are six of
us now! There should only be five, but there are six.
Count! Count, I tell you! Six!"
To Mort it seemed that a gigantic spider was racing
across the web of their thoughts….
See also this journal on May 30– "720 in the Book"– and on May 31– "Memorial for Galois."
("Obnoxious nerds"— a phrase Martin Gardner recently applied to Galois— will note that 720
Significant Passage:
On the Writing Style of Visual Thinkers
"The words are filled with unstated meaning.
They are (the term is Ricoeur's) 'packed'
and need unpacking." —Gerald Grow
From the date of Ricoeur's death,
May 20, 2005—
“Plato’s most significant passage
may be found in Phaedrus 265b…."
|
With a little effort, cross-referenced." — Opening sentence
|
Mozart's K 265 is variations on the theme
now known as "Twinkle, Twinkle, Little Star."
For darker variations on the Twinkle theme,
see the film "Joshua" and Martin Gardner's
Annotated Alice (Norton, 2000, pp. 73-75).

For darker variations on the asterisk theme,
see Darkness Visible (May 25)
and Vonnegut's Asterisk.
From Ursula K. Le Guin’s novel
The Dispossessed: An Ambiguous Utopia (1974)—
Chapter One
“There was a wall. It did not look important. It was built of uncut rocks roughly mortared. An adult could look right over it, and even a child could climb it. Where it crossed the roadway, instead of having a gate it degenerated into mere geometry, a line, an idea of boundary. But the idea was real. It was important. For seven generations there had been nothing in the world more important than that wall.
Like all walls it was ambiguous, two-faced. What was inside it and what was outside it depended upon which side of it you were on.”
Note—
“We note that the phrase ‘instead of having a gate it degenerated into mere geometry’ is mere fatuousness. If there is an idea here, degenerate, mere, and geometry in concert do not fix it. They bat at it like a kitten at a piece of loose thread.”
— Samuel R. Delany, The Jewel-Hinged Jaw: Notes on the Language of Science Fiction (Dragon Press, 1977), page 110 of revised edition, Wesleyan University Press, 2009
(For the phrase mere geometry elsewhere, see a note of April 22. The apparently flat figures in that note’s illustration “Galois Affine Geometry” may be regarded as degenerate views of cubes.)
Later in the Le Guin novel—
“… The Terrans had been intellectual imperialists, jealous wall builders. Even Ainsetain, the originator of the theory, had felt compelled to give warning that his physics embraced no mode but the physical and should not be taken as implying the metaphysical, the philosophical, or the ethical. Which, of course, was superficially true; and yet he had used number, the bridge between the rational and the perceived, between psyche and matter, ‘Number the Indisputable,’ as the ancient founders of the Noble Science had called it. To employ mathematics in this sense was to employ the mode that preceded and led to all other modes. Ainsetain had known that; with endearing caution he had admitted that he believed his physics did, indeed, describe reality.
Strangeness and familiarity: in every movement of the Terran’s thought Shevek caught this combination, was constantly intrigued. And sympathetic: for Ainsetain, too, had been after a unifying field theory. Having explained the force of gravity as a function of the geometry of spacetime, he had sought to extend the synthesis to include electromagnetic forces. He had not succeeded. Even during his lifetime, and for many decades after his death, the physicists of his own world had turned away from his effort and its failure, pursuing the magnificent incoherences of quantum theory with its high technological yields, at last concentrating on the technological mode so exclusively as to arrive at a dead end, a catastrophic failure of imagination. Yet their original intuition had been sound: at the point where they had been, progress had lain in the indeterminacy which old Ainsetain had refused to accept. And his refusal had been equally correct– in the long run. Only he had lacked the tools to prove it– the Saeba variables and the theories of infinite velocity and complex cause. His unified field existed, in Cetian physics, but it existed on terms which he might not have been willing to accept; for the velocity of light as a limiting factor had been essential to his great theories. Both his Theories of Relativity were as beautiful, as valid, and as useful as ever after these centuries, and yet both depended upon a hypothesis that could not be proved true and that could be and had been proved, in certain circumstances, false.
But was not a theory of which all the elements were provably true a simple tautology? In the region of the unprovable, or even the disprovable, lay the only chance for breaking out of the circle and going ahead.
In which case, did the unprovability of the hypothesis of real coexistence– the problem which Shevek had been pounding his head against desperately for these last three days. and indeed these last ten years– really matter?
He had been groping and grabbing after certainty, as if it were something he could possess. He had been demanding a security, a guarantee, which is not granted, and which, if granted, would become a prison. By simply assuming the validity of real coexistence he was left free to use the lovely geometries of relativity; and then it would be possible to go ahead. The next step was perfectly clear. The coexistence of succession could be handled by a Saeban transformation series; thus approached, successivity and presence offered no antithesis at all. The fundamental unity of the Sequency and Simultaneity points of view became plain; the concept of interval served to connect the static and the dynamic aspect of the universe. How could he have stared at reality for ten years and not seen it? There would be no trouble at all in going on. Indeed he had already gone on. He was there. He saw all that was to come in this first, seemingly casual glimpse of the method, given him by his understanding of a failure in the distant past. The wall was down. The vision was both clear and whole. What he saw was simple, simpler than anything else. It was simplicity: and contained in it all complexity, all promise. It was revelation. It was the way clear, the way home, the light.”
Related material—
Time Fold, Halloween 2005, and May and Zan.
See also The Devil and Wallace Stevens—
“In a letter to Harriet Monroe, written December 23, 1926, Stevens refers to the Sapphic fragment that invokes the genius of evening: ‘Evening star that bringest back all that lightsome Dawn hath scattered afar, thou bringest the sheep, thou bringest the goat, thou bringest the child home to the mother.’ Christmas, writes Stevens, ‘is like Sappho’s evening: it brings us all home to the fold’ (Letters of Wallace Stevens, 248).”
— “The Archangel of Evening,” Chapter 5 of Wallace Stevens: The Intensest Rendezvous, by Barbara M. Fisher, The University Press of Virginia, 1990
"The eye you see him with is the same
eye with which he sees you."
– Father Egan on page 333
of Robert Stone's A Flag for Sunrise
(Knopf hardcover, 1981)
Part I– Bounded in a Nutshell

Ian McKellen at a mental hospital's diamond-shaped window in "Neverwas"
Part II– The Royal Castle
Ian McKellen at his royal castle's diamond-shaped window in "Neverwas"
Part III– King of Infinite Space

H.S.M. Coxeter crowns himself "King of Infinite Space"
Related material:
See Coxeter in this journal.
Where Entertainment is God, continued—
The following paragraphs are from a review by Piotr Siemion of Infinite Jest, a novel by David Foster Wallace. Illustrations have been added.
"Wallace was somehow able to twist together three yarns…. …there's a J.D Salinger for those who like J.D. Salinger. There's William Burroughs for those hardy souls who like some kick in their prose. And there's a dash of Kurt Vonnegut too. All three voices, though, are amplified in Infinite Jest beyond mere distortion and then projected onto Wallace's peculiar own three-ring circus….
… there's entertainment. Make it a capital E.
Illustration by Clint Eastwood
from Log24 post "E is for Everlast"
Infinite Jest revolves, among its many gyrations, around the story of the Entertainment, a film-like creation going by the title of 'Infinite Jest' and created shortly before his suicidal death by the young tennis star's father. The Entertainment's copies are now being disseminated clandestinely all over Wallace's funny America. Problem is, of course, that the film is too good. Anybody who gets to watch it becomes hooked instantly and craves only to watch it again, and again, and again, until the audience drops dead of exhaustion and hunger. Why eat when you're entertained by such a good movie? Wallace's premise brings you back to that apocryphal lab experiment in which rats were treated to a similar choice. When the rat pushed one button, marked FOOD, it would get a food pellet. The other button, marked FUN, would fire up an electrode rigged right into the orgasm center somewhere in the rat's cortex. Needless to add, one rat after another would drop dead from hunger, still twitching luridly and trying to finesse one last push of the button. Same thing in Wallace's story, especially that even those characters who have not seen the Entertainment yet, keep on entertaining themselves by different means."
The title of the Entertainment, "Infinite Jest," might also be applied to a BBC program featuring mathematician Peter J. Cameron. The program's actual title was "To Infinity and Beyond." It was broadcast the night of Feb. 10 (the date of this journal's previous post).
Few, however, are likely to find the Infinity program addictive. For closer approaches to Wallace's ideal Entertainment, see instead Dante (in the context of this journal's Feb. 4 posts on Cameron and the afterlife) and the BBC News.
From Peter J. Cameron's weblog today—
According to the Buddha,
Scholars speak in sixteen ways of the state of the soul after death. They say that it has form or is formless; has and has not form, or neither has nor has not form; it is finite or infinite; or both or neither; it has one mode of consciousness or several; has limited consciousness or infinite; is happy or miserable; or both or neither.
He does go on to say that such speculation is unprofitable; but bear with me for a moment.
With logical constructs such as “has and has not form, or neither has nor has not form”, it is perhaps a little difficult to see what is going on. But, while I hesitate to disagree with the Compassionate One, I think there are more than sixteen possibilities described here: how many?
Cameron's own answer (from problem solutions for his book Combinatorics)–
One could argue here that the numbers of choices should be multiplied, not added; there are 4 choices for form, 4 for finiteness, 2 for modes of consciousness, 2 for finiteness of consciousness, and 4 for happiness, total 28 = 256. (You may wish to consider whether all 256 are really possible.)
Related material– "What is 256 about?"
Some partial answers–
April 2, 2003 — The Question (lottery number)
May 2, 2003 — Zen and Language Games (page number)
August 4, 2003 — Venn's Trinity (power of two)
September 28, 2005 — Mathematical Narrative (page number)
October 26, 2005 — Human Conflict Number Five (chronomancy)
June 23, 2006 — Binary Geometry (power of two)
July 23, 2006 — Partitions (power of two)
October 3, 2006 — Hard Lessons (number of pages,
as counted in one review)
October 10, 2006 — Mate (lottery number)
October 8, 2008 — Serious Numbers (page number)
Quoted here Nov. 10, 2009—
Epigraphs at
Peter Cameron’s home page:

The Galois Quaternion
|
I had foreseen it all in precise detail. i = an imaginary being Here, on this complex space, |
Related material:
The Galois Quaternion
Click for context.
(See also Nativity and the end
of this morning's post.)
"L’unité jointe à l’infini ne l’augmente de rien, non plus qu’un pied à une mesure infinie. Le fini s’anéantit en présence de l’infini, et devient un pur néant….
Nous connaissons qu’il y a un infini, et ignorons sa nature. Comme nous savons qu’il est faux que les nombres soient finis, donc il est vrai qu’il y a un infini en nombre. Mais nous ne savons ce qu’il est: il est faux qu’il soit pair, il est faux qu’il soit impair; car, en ajoutant 1 unité, il ne change point de nature; cependant c’est un nombre, et tout nombre est pair ou impair (il est vrai que cela s’entend de tout nombre fini). Ainsi…."
"Unity joined to infinity adds nothing to it, no more than one foot to an infinite measure. The finite is annihilated in the presence of the infinite, and becomes a pure nothing….
We know that there is an infinite, and are ignorant of its nature. As we know it to be false that numbers are finite, it is therefore true that there is an infinity in number. But we do not know what it is. It is false that it is even, it is false that it is odd; for the addition of a unit can make no change in its nature. Yet it is a number, and every number is odd or even (this is certainly true of every finite number). So…."
— Pensées (trans. W. F. Trotter), Courier Dover Publications, 2003
Un Pur Néant:
"So did God cause the big bang?
Overcome by metaphysical lassitude,
I finally reach over to my bookshelf
for The Devil's Bible.
Turning to Genesis I read:
'In the beginning
there was nothing.
And God said,
'Let there be light!'
And there was still nothing,
but now you could see it.'"
— Jim Holt, Big-Bang Theology,
Slate's "High Concept" department

Ainsi….
"In the garden of Adding,
Live Even and Odd"
— E. L. Doctorow


The above was, like the
previous entry, suggested by
this morning’s monumentally
tasteless NY Times obit page.
The author of the
“pleasantly discursive”
remark has been called both
“King of Geometry” and
“King of Infinite Space.”
He lived in Toronto.
Detail of this morning’s Times
(click for larger version) —
(Corcoran.com is the website of
a New York City real estate firm.
Today’s Bing.com search image is
a view of the city from Central Park.)
“We keep coming back
and coming back/To the real….”
— Wallace Stevens
Through the
Looking Glass:
A Sort of Eternity
From the new president’s inaugural address:
“… in the words of Scripture, the time has come to set aside childish things.”
The words of Scripture:
“through a glass”—
[di’ esoptrou].
By means of
a mirror [esoptron].
Childish things:

Not-so-childish:
Three planes through
the center of a cube
that split it into
eight subcubes:

Through a glass, darkly:
A group of 8 transformations is
generated by affine reflections
in the above three planes.
Shown below is a pattern on
the faces of the 2x2x2 cube
that is symmetric under one of
these 8 transformations–
a 180-degree rotation:
(Click on image
for further details.)
But then face to face:
A larger group of 1344,
rather than 8, transformations
of the 2x2x2 cube
is generated by a different
sort of affine reflections– not
in the infinite Euclidean 3-space
over the field of real numbers,
but rather in the finite Galois
3-space over the 2-element field.

Galois age fifteen,
drawn by a classmate.
These transformations
in the Galois space with
finitely many points
produce a set of 168 patterns
like the one above.
For each such pattern,
at least one nontrivial
transformation in the group of 8
described above is a symmetry
in the Euclidean space with
infinitely many points.
For some generalizations,
see Galois Geometry.
Related material:
The central aim of Western religion–
"Each of us has something to offer the Creator... the bridging of masculine and feminine, life and death. It's redemption.... nothing else matters." -- Martha Cooley in The Archivist (1998) The central aim of Western philosophy– Dualities of Pythagoras as reconstructed by Aristotle: Limited Unlimited Odd Even Male Female Light Dark Straight Curved ... and so on .... “Of these dualities, the first is the most important; all the others may be seen as different aspects of this fundamental dichotomy. To establish a rational and consistent relationship between the limited [man, etc.] and the unlimited [the cosmos, etc.] is… the central aim of all Western philosophy.” — Jamie James in The Music of the Spheres (1993) “In the garden of Adding — The Midrash Jazz Quartet in City of God, by E. L. Doctorow (2000) A quotation today at art critic Carol Kino’s website, slightly expanded: “Art inherited from the old religion — Octavio Paz,”Seeing and Using: Art and Craftsmanship,” in Convergences: Essays on Art and Literature (New York: Harcourt Brace Jovanovich 1987), 52 From Brian O’Doherty’s 1976 Artforum essays– not on museums, but rather on gallery space: “We have now reached
“Space: what you — James Joyce, Ulysses |
“Somehow it seems to fill my head with ideas– only I don’t exactly know what they are!…. Let’s have a look at the garden first!”
— A passage from Lewis Carroll’s Through the Looking-Glass. The “garden” part– but not the “ideas” part– was quoted by Jacques Derrida in Dissemination in the epigraph to Chapter 7, “The Time before First.”
“‘For you… he… we aren’t meaning…’ She was almost stammering, as if she were trying to say several things at once…. Suddenly she gave a little tortured scream. ‘O!’ she cried, ‘O! I can’t keep up! it keeps dividing! There’s too many things to think of!'”
— A passage from Charles Williams’s The Place of the Lion, Chapter 12.
“He was thinking faster than he had ever done, and questions rose out of nothing and followed each other– what was to will? Will was determination to choose– what was choice? How could there be choice, unless there was preference, and if there was preference there was no choice, for it was not possible to choose against that preferring nature which was his being; yet being consisted in choice, for only by taking and doing this and not that could being know itself, could it indeed be; to be then consisted in making an inevitable choice, and all that was left was to know the choice, yet even then was the chosen thing the same as the nature that chose, and if not… So swiftly the questions followed each other that he seemed to be standing in flashing coils of subtlety, an infinite ring of vivid intellect and more than intellect, for these questions were not of the mind alone but absorbed into themselves physical passion and twined through all his nature on an unceasing and serpentine journey.”
— A passage from The Place of the Lion, Chapter 10.
— Good Will Hunting
— T. S. Eliot, “The Waste Land“
“In the Roman Catholic tradition, the term ‘Body of Christ’ refers not only to the body of Christ in the spiritual realm, but also to two distinct though related things: the Church and the reality of the transubstantiated bread of the Eucharist….
According to the Catechism of the Catholic Church, ‘the comparison of the Church with the body casts light on the intimate bond between Christ and his Church. Not only is she gathered around him; she is united in him, in his body….’
….To distinguish the Body of Christ in this sense from his physical body, the term ‘Mystical Body of Christ’ is often used. This term was used as the first words, and so as the title, of the encyclical Mystici Corporis Christi of Pope Pius XII.”
Pope Pius XII:
“83. The Sacrament of the Eucharist is itself a striking and wonderful figure of the unity of the Church, if we consider how in the bread to be consecrated many grains go to form one whole, and that in it the very Author of supernatural grace is given to us, so that through Him we may receive the spirit of charity in which we are bidden to live now no longer our own life but the life of Christ, and to love the Redeemer Himself in all the members of His social Body.”
Log24 on this date in 2002:
Religious Symbolism
at Princeton
as well as
and a
“striking and wonderful figure”
from this morning’s newspaper–

|
"Credences of Summer," VII,
by Wallace Stevens, from
"Three times the concentred |
One possibility —
Bertram Kostant, Professor Emeritus of Mathematics at MIT, on an object discussed in a recent New Yorker:
"A word about E(8). In my opinion, and shared by others, E(8) is the most magnificent 'object' in all of mathematics. It is like a diamond with thousands of facets. Each facet offering a different view of its unbelievable intricate internal structure."
Another possibility —

A more modest object —
the 4×4 square.
Update of Aug. 20-21 —
Kostant's poetic comparison might be applied also to this object.
More precisely, there are 322,560 natural rearrangements– which a poet might call facets*— of the array, each offering a different view of the array's internal structure– encoded as a unique ordered pair of symmetric graphic designs. The symmetry of the array's internal structure is reflected in the symmetry of the graphic designs. For examples, see the Diamond 16 Puzzle.
For an instance of Stevens's "three times" process, see the three parts of the 2004 web page Ideas and Art.
* For the metaphor of rearrangements as facets, note that each symmetry (rearrangement) of a Platonic solid corresponds to a rotated facet: the number of symmetries equals the number of facets times the number of rotations (edges) of each facet–

If Greek geometers had started with a finite space (as in The Eightfold Cube), the history of mathematics might have dramatically illustrated Halmos's saying (Aug. 16) that
"The problem is– the genius is– given an infinite question, to think of the right finite question to ask. Once you thought of the finite answer, then you would know the right answer to the infinite question."
The Greeks, of course, answered the infinite questions first– at least for Euclidean space. Halmos was concerned with more general modern infinite spaces (such as Hilbert space) where the intuition to be gained from finite questions is still of value.
Seeing the Finite Structure
The following supplies some context for remarks of Halmos on combinatorics.
From Paul Halmos: Celebrating 50 years of Mathematics, by John H. Ewing, Paul Richard Halmos, Frederick W. Gehring, published by Springer, 1991–
Interviews with Halmos, “Paul Halmos by Parts,” by Donald J. Albers–
“Part II: In Touch with God*“– on pp. 27-28:
The Root of All Deep Mathematics
“Albers. In the conclusion of ‘Fifty Years of Linear Algebra,’ you wrote: ‘I am inclined to believe that at the root of all deep mathematics there is a combinatorial insight… I think that in this subject (in every subject?) the really original, really deep insights are always combinatorial, and I think for the new discoveries that we need– the pendulum needs– to swing back, and will swing back in the combinatorial direction.’ I always thought of you as an analyst.
Halmos: People call me an analyst, but I think I’m a born algebraist, and I mean the same thing, analytic versus combinatorial-algebraic. I think the finite case illustrates and guides and simplifies the infinite.
Some people called me full of baloney when I asserted that the deep problems of operator theory could all be solved if we knew the answer to every finite dimensional matrix question. I still have this religion that if you knew the answer to every matrix question, somehow you could answer every operator question. But the ‘somehow’ would require genius. The problem is not, given an operator question, to ask the same question in finite dimensions– that’s silly. The problem is– the genius is– given an infinite question, to think of the right finite question to ask. Once you thought of the finite answer, then you would know the right answer to the infinite question.
Combinatorics, the finite case, is where the genuine, deep insight is. Generalizing, making it infinite, is sometimes intricate and sometimes difficult, and I might even be willing to say that it’s sometimes deep, but it is nowhere near as fundamental as seeing the finite structure.”

Whether the above sketch of the passage from operator theory to harmonic analysis to Walsh functions to finite geometry can ever help find “the right finite question to ask,” I do not know. It at least suggests that finite geometry (and my own work on models in finite geometry) may not be completely irrelevant to mathematics generally regarded as more deep.
* See the Log24 entries following Halmos’s death.
On this date in 1961,
Ernest Hemingway shot
himself.

The Talented Patricia Highsmith
Related material:
The Languages of Addiction,
Ch. 13: The Barnes Complex
See also
The Garden of Eden.
The conclusion of yesterday’s commentary on the May 30-31 Pennsylvania Lottery numbers:
Thomas Pynchon, Gravity’s Rainbow:
“The fear balloons again inside his brain. It will not be kept down with a simple Fuck You…. A smell, a forbidden room, at the bottom edge of his memory. He can’t see it, can’t make it out. Doesn’t want to. It is allied with the Worst Thing.
He knows what the smell has to be: though according to these papers it would have been too early for it, though he has never come across any of the stuff among the daytime coordinates of his life, still, down here, back here in the warm dark, among early shapes where the clocks and calendars don’t mean too much, he knows that’s what haunting him now will prove to be the smell of Imipolex G.
Then there’s this recent dream he is afraid of having again. He was in his old room, back home. A summer afternoon of lilacs and bees and
286”
What are we to make of this enigmatic 286? (No fair peeking at page 287.)
One possible meaning, given The Archivist‘s claim that “existence is infinitely cross-referenced”–
Page 286 of Ernest G. Schachtel, Metamorphosis: On the Conflict of Human Development and the Psychology of Creativity (first published in 1959), Hillsdale NJ and London, The Analytic Press, 2001 (chapter– “On Memory and Childhood Amnesia”):
“Both Freud and Proust speak of the autobiographical [my italics] memory, and it is only with regard to this memory that the striking phenomenon of childhood amnesia and the less obvious difficulty of recovering any past experience may be observed.”
The concluding “summer afternoon of lilacs and bees” suggests that 286 may also be a chance allusion to the golden afternoon of Disney’s Alice in Wonderland. (Cf. St. Sarah’s Day, 2008)
Some may find the Disney afternoon charming; others may see it as yet another of Paul Simon’s dreaded cartoon graveyards.
More tastefully, there is poem 286 in the 1919 Oxford Book of English Verse– “Love.”
For a midrash on this poem, see Simone Weil, who became acquainted with the poem by chance:
“I always prefer saying chance rather than Providence.”
— Simone Weil, letter of about May 15, 1942
Weil’s brother André might prefer Providence (source of the Bulletin of the American Mathematical Society.)
 (Photo from Providence)
(Photo from Providence)
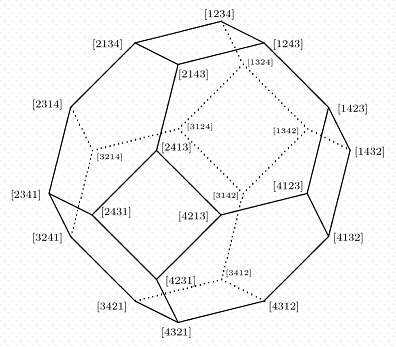
For more on the mathematical significance of this figure, see (for instance) Happy Birthday, Hassler Whitney, and Combinatorics of Coxeter Groups, by Anders Björner and Francesco Brenti, Graduate Texts in Mathematics, vol. 231, Springer, New York, 2005.
This book is reviewed in the current issue (July 2008) of the above-mentioned Providence Bulletin.
The review in the Bulletin discusses reflection groups in continuous spaces.
From Saturday's entry
(Log24, Dec. 22, 2007)
a link goes to–
The five entries of June 14, 2007.
From there, the link
"One Two Three Four,
Who Are We For?"
goes to–
Princeton: A Whirligig Tour
(Log24, June 5, 2007).
From there, the link
"Taking Christ to Studio 60"
goes to–
The five Log 24 entries
prior to midnight Sept. 18, 2006.
From there, the link
"Log24, January 18, 2004"
goes to–
A Living Church.
From there, the link
"click here"
goes to–
In the Bleak Midwinter
(Internet Movie Database)…
Tagline:
The drama. The passion. The intrigue… And the rehearsals haven't even started.
Plot Summary:
Out of work actor Joe volunteers to help try and save his sister's local church
for the community by putting on a Christmas production of Hamlet…
"… were it not that
I have bad dreams."
— Hamlet
Related material:
The New York Times online
obituaries of December 22,
Ike Turner's
"Bad Dreams" album
(see Log24, July 12, 2004),
"Devil Music," a composition
by H. S. M. Coxeter,
and
Those desiring more literary depth
may consult the G. K. Chesterton
play "Magic" for which Coxeter
wrote his "Devil Music" and
the Ingmar Bergman film
"The Magician" said to have
been inspired by Chesterton.
Rudolf Arnheim, a student of Gestalt psychology (which, an obituary notes, emphasizes "the perception of forms as organized wholes") was the first Professor of the Psychology of Art at Harvard. He died at 102 on Saturday, June 9, 2007.
The conclusion of yesterday's New York Times obituary of Arnheim:
"… in The New York Times Book Review in 1986, Celia McGee called Professor Arnheim 'the best kind of romantic,' adding, 'His wisdom, his patient explanations and lyrical enthusiasm are those of a teacher.'"
A related quotation:
"And you are teaching them a thing or two about yourself. They are learning that you are the living embodiment of two timeless characterizations of a teacher: 'I say what I mean, and I mean what I say' and 'We are going to keep doing this until we get it right.'"
Here, yet again, is an illustration that has often appeared in Log24– notably, on the date of Arnheim's death:

Related quotations:
"We have had a gutful of fast art and fast food. What we need more of is slow art: art that holds time as a vase holds water: art that grows out of modes of perception and whose skill and doggedness make you think and feel; art that isn't merely sensational, that doesn't get its message across in 10 seconds, that isn't falsely iconic, that hooks onto something deep-running in our natures. In a word, art that is the very opposite of mass media. For no spiritually authentic art can beat mass media at their own game."
— Robert Hughes, speech of June 2, 2004
"Whether the 3×3 square grid is fast art or slow art, truly or falsely iconic, perhaps depends upon the eye of the beholder."
If the beholder is Rudolf Arnheim, whom we may now suppose to be viewing the above figure in the afterlife, the 3×3 square is apparently slow art. Consider the following review of his 1982 book The Power of the Center:
"Arnheim deals with the significance of two kinds of visual organization, the concentric arrangement (as exemplified in a bull's-eye target) and the grid (as exemplified in a Cartesian coordinate system)….
It is proposed that the two structures of grid and target are the symbolic vehicles par excellence for two metaphysical/psychological stances. The concentric configuration is the visual/structural equivalent of an egocentric view of the world. The self is the center, and all distances exist in relation to the focal spectator. The concentric arrangement is a hermetic, impregnable pattern suited to conveying the idea of unity and other-worldly completeness. By contrast, the grid structure has no clear center, and suggests an infinite, featureless extension…. Taking these two ideal types of structural scaffold and their symbolic potential (cosmic, egocentric vs. terrestrial, uncentered) as given, Arnheim reveals how their underlying presence organizes works of art."
— Review of Rudolf Arnheim's The Power of the Center: A Study of Composition in the Visual Arts (Univ. of Calif. Press, 1982). Review by David A. Pariser, Studies in Art Education, Vol. 24, No. 3 (1983), pp. 210-213
Arnheim himself says in this book (pp. viii-ix) that "With all its virtues, the framework of verticals and horizontals has one grave defect. It has no center, and therefore it has no way of defining any particular location. Taken by itself, it is an endless expanse in which no one place can be distinguished from the next. This renders it incomplete for any mathematical, scientific, and artistic purpose. For his geometrical analysis, Descartes had to impose a center, the point where a pair of coordinates [sic] crossed. In doing so he borrowed from the other spatial system, the centric and cosmic one."
Students of art theory should, having read the above passages, discuss in what way the 3×3 square embodies both "ideal types of structural scaffold and their symbolic potential."
We may imagine such a discussion in an afterlife art class– in, perhaps, Purgatory rather than Heaven– that now includes Arnheim as well as Ernst Gombrich and Kirk Varnedoe.
Such a class would be one prerequisite for a more advanced course– Finite geometry of the square and cube.
"I have another far more solid and central ground for submitting to it as a faith, instead of merely picking up hints from it as a scheme. And that is this: that the Christian Church in its practical relation to my soul is a living teacher, not a dead one. It not only certainly taught me yesterday, but will almost certainly teach me to-morrow. Once I saw suddenly the meaning of the shape of the cross; some day I may see suddenly the meaning of the shape of the mitre. One free morning I saw why windows were pointed; some fine morning I may see why priests were shaven. Plato has told you a truth; but Plato is dead. Shakespeare has startled you with an image; but Shakespeare will not startle you with any more. But imagine what it would be to live with such men still living, to know that Plato might break out with an original lecture to-morrow, or that at any moment Shakespeare might shatter everything with a single song. The man who lives in contact with what he believes to be a living Church is a man always expecting to meet Plato and Shakespeare to-morrow at breakfast. He is always expecting to see some truth that he has never seen before."
— G. K. Chesterton, Orthodoxy, Ch. IX
From Plato, Pegasus, and the Evening Star (11/11/99):
|
"Nonbeing must in some sense be, otherwise what is it that there is not? This tangled doctrine might be nicknamed Plato's beard; historically it has proved tough, frequently dulling the edge of Occam's razor…. I have dwelt at length on the inconvenience of putting up with it. It is time to think about taking steps." "The Consul could feel his glance at Hugh becoming a cold look of hatred. Keeping his eyes fixed gimlet-like upon him he saw him as he had appeared that morning, smiling, the razor edge keen in sunlight. But now he was advancing as if to decapitate him." |
"O God, I could be
bounded in a nutshell
and count myself
a king of infinite space,
were it not that
I have bad dreams."
— Hamlet
From today's newspaper:

Notes:
For an illustration of
the phrase "solid and central,"
see the previous entry.
For further context, see the
five Log24 entries ending
on September 6, 2006.
For background on the word
"hollow," see the etymology of
"hole in the wall" as well as
"The God-Shaped Hole" and
"Is Nothing Sacred?"
For further ado, see
Macbeth, V.v
("signifying nothing")
and The New Yorker,
issue dated tomorrow.
Today is the 21st birthday of my note “The Relativity Problem in Finite Geometry.”
Some relevant quotations:
“This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them.”
— Hermann Weyl, The Classical Groups, Princeton University Press, 1946, p. 16
Describing the branch of mathematics known as Galois theory, Weyl says that it
“… is nothing else but the relativity theory for the set Sigma, a set which, by its discrete and finite character, is conceptually so much simpler than the infinite set of points in space or space-time dealt with by ordinary relativity theory.”
— Weyl, Symmetry, Princeton University Press, 1952, p. 138
Weyl’s set Sigma is a finite set of complex numbers. Some other sets with “discrete and finite character” are those of 4, 8, 16, or 64 points, arranged in squares and cubes. For illustrations, see Finite Geometry of the Square and Cube. What Weyl calls “the relativity problem” for these sets involves fixing “objectively” a class of equivalent coordinatizations. For what Weyl’s “objectively” means, see the article “Symmetry and Symmetry Breaking,” by Katherine Brading and Elena Castellani, in the Stanford Encyclopedia of Philosophy:
“The old and natural idea that what is objective should not depend upon the particular perspective under which it is taken into consideration is thus reformulated in the following group-theoretical terms: what is objective is what is invariant with respect to the transformation group of reference frames, or, quoting Hermann Weyl (1952, p. 132), ‘objectivity means invariance with respect to the group of automorphisms [of space-time].‘[22]
22. The significance of the notion of invariance and its group-theoretic treatment for the issue of objectivity is explored in Born (1953), for example. For more recent discussions see Kosso (2003) and Earman (2002, Sections 6 and 7).
References:
Born, M., 1953, “Physical Reality,” Philosophical Quarterly, 3, 139-149. Reprinted in E. Castellani (ed.), Interpreting Bodies: Classical and Quantum Objects in Modern Physics, Princeton, NJ: Princeton University Press, 1998, pp. 155-167.
Earman, J., 2002, “Laws, Symmetry, and Symmetry Breaking; Invariance, Conservation Principles, and Objectivity,’ PSA 2002, Proceedings of the Biennial Meeting of the Philosophy of Science Association 2002, forthcoming [Abstract/Preprint available online]
Kosso, P., 2003, “Symmetry, objectivity, and design,” in K. Brading and E. Castellani (eds.), Symmetries in Physics: Philosophical Reflections, Cambridge: Cambridge University Press, pp. 410-421.
Weyl, H., 1952, Symmetry, Princeton, NJ: Princeton University Press.
See also
Archives Henri Poincaré (research unit UMR 7117, at Université Nancy 2, of the CNRS)–
“Minkowski, Mathematicians, and the Mathematical Theory of Relativity,” by Scott Walter, in The Expanding Worlds of General Relativity (Einstein Studies, volume 7), H. Goenner, J. Renn, J. Ritter and T. Sauer, editors, Boston/Basel: Birkhäuser, 1999, pp. 45-86–
“Developing his ideas before Göttingen mathematicians in April 1909, Klein pointed out that the new theory based on the Lorentz group (which he preferred to call ‘Invariantentheorie’) could have come from pure mathematics (1910: 19). He felt that the new theory was anticipated by the ideas on geometry and groups that he had introduced in 1872, otherwise known as the Erlangen program (see Gray 1989: 229).”
References:
Gray, Jeremy J. (1989). Ideas of Space. 2d ed. Oxford: Oxford University Press.
Klein, Felix. (1910). “Über die geometrischen Grundlagen der Lorentzgruppe.” Jahresbericht der deutschen Mathematiker-Vereinigung 19: 281-300. [Reprinted: Physikalische Zeitschrift 12 (1911): 17-27].
Related material: A pathetically garbled version of the above concepts was published in 2001 by Harvard University Press. See Invariances: The Structure of the Objective World, by Robert Nozick.
“At times, bullshit can only be
countered with superior bullshit.”
— Norman Mailer
“It may be that universal history is the
history of the different intonations
given a handful of metaphors.”
— Jorge Luis Borges (1951),
“The Fearful Sphere of Pascal,”
in Labyrinths, New Directions, 1962
— Joseph A. Goguen, “Ontology, Society, and Ontotheology” (pdf)
Goguen does not give a source for this alleged “thoughts of God” statement.
A Web search for the source leads only to A Mathematical Journey, by Stanley Gudder, who apparently also attributes the saying to Euclid.
Neither Goguen nor Gudder seems to have had any interest in the accuracy of the Euclid attribution.
Talk of “nature” and “God” seems unlikely from Euclid, a pre-Christian Greek whose pure mathematics has (as G. H. Hardy might be happy to point out) little to do with either.
Loose talk about God’s thoughts has also been attributed to Kepler and Einstein… and we all know about Stephen Hawking.
Gudder may have been misquoting some other author’s blather about Kepler. Another possible source of the “thoughts of God” phrase is Hans Christian Oersted. The following is from Oersted’s The Soul in Nature—
“Sophia. Nothing of importance; though indeed I had one question on my lips when the conversion took the last turn. When you alluded to the idea, that the Reason manifested in Nature is infallible, while ours is fallible, should you not rather have said, that our Reason accords with that of Nature, as that in the voice of Nature with ours?
Alfred. Each of these interpretations may be justified by the idea to which it applies, whether we start from ourselves or external nature. There are yet other ways of expressing it; for instance, the laws of Nature are the thoughts of Nature.
Sophia. Then these thoughts of Nature are also thoughts of God.
Alfred. Undoubtedly so, but however valuable the expression may be, I would rather that we should not make use of it till we are convinced that our investigation leads to a view of Nature, which is also the contemplation of God. We shall then feel justified by a different and more perfect knowledge to call the thoughts of Nature those of God; I therefore beg you will not proceed to [sic] fast.”
Oersted also allegedly said that “The Universe is a manifestation of an Infinite Reason and the laws of Nature are the thoughts of God.” This remark was found (via Google book search) in an obscure journal that does not give a precise source for the words it attributes to Oersted.

(continued from
January 9, 2003)
George Balanchine
|
"What on earth is
a concrete universal?"
— Robert M. Pirsig
Review:
From Wikipedia's
"Upper Ontology"
and
Epiphany 2007:
"There is no neutral ground
that can serve as
a means of translating between
specialized (lower) ontologies."
There is, however,
"the field of reason"–
the 3×3 grid:
Click on grid
for details.
As Rosalind Krauss
has noted, some artists
regard the grid as
"a staircase to
the Universal."
Other artists regard
Epiphany itself as an
approach to
the Universal:
— Richard Kearney, 2005,
in The New Arcadia Review
Kearney (right) with
Martin Scorsese (left)
and Gregory Peck
in 1997.
— Richard Kearney, interview (pdf) in The Leuven Philosophy Newsletter, Vol. 14, 2005-2006
For more on "the possible," see Kearney's The God Who May Be, Diamonds Are Forever, and the conclusion of Mathematics and Narrative:
|
"We symbolize
logical necessity with the box and logical possibility with the diamond
"The possibilia that exist,
— Michael Sudduth, |
Putting the
X
in Xmas

|
“In one of Jorge Luis Borges’s best-known short stories, ‘Pierre Menard, Author of the Quixote,’ a 20th-century French writer sets out to compose a verbatim copy of Cervantes’s 17th-century masterpiece simply because he thinks he can, originality perhaps not being all it’s cracked up to be. He manages two chapters word for word, a spontaneous duplicate that Borges’s narrator finds to be ‘infinitely richer’ than the original because it contains all manner of new meanings and inflections, wrenched as it is from its proper time and context….”
[An artist’s version of a newspaper is]…. “a drawing of a copy of a version of what happened, holding a mirror up to nature with a refraction or two in between. In a way that mixes Borges with a dollop of Jean Baudrillard and a heavy helping of Walter Benjamin, the work also upends ideas….” |
The Work:
Pennsylvania Lottery
December 2006
Daily Number (Day):
| Borges, Menard’s Quixote, and The Harvard Crimson |
Mon., Dec. 11: 133 |
| Baudrillard (via a white Matrix) |
Sun., Dec. 10: 569 |
| Benjamin and a black view of life in “The Garden of Allah” |
Sat., Dec. 9: 602 |
Click on numbers
for commentary.
“There is nothing new under the sun. With the death of the real, or rather with its (re)surrection, hyperreality both emerges and is already always reproducing itself.” –Jean Baudrillard

The texts in question are said
to be manuscripts of
“Pierre Menard, Author of the Quixote,”
and “The Library of Babel.”
The latter deals (like
“The Mountains of Pi“)
with literature that can
be seen as the result
of a random process–
such as the lottery in
another story by Borges.
A less sinister lottery
is that of Pennsylvania–
known to some as
“the Keystone State.”
I prefer to think of it as
“the State of Grace.”

The “NITE” number 108 leads us
naturally to 1/08:
| Sunday, January 08, 2006
|
Another figure from 1/08,
St. Mary Magdalene, might,
adapting the words of Borges,
offer the following observation:
“Shakespeare’s text and the lottery’s
are verbally identical, but the second
is almost infinitely richer.
(More ambiguous, detractors will
say, but ambiguity is richness.)”
Related material: 11/22.
Geometry
from Point
to Hyperspace
by Steven H. Cullinane
Euclid is “the most famous
geometer ever known
and for good reason:
for millennia it has been
his window
that people first look through
when they view geometry.”
— Euclid’s Window:
The Story of Geometry
from Parallel Lines
to Hyperspace,
by Leonard Mlodinow
“…the source of
all great mathematics
is the special case,
the concrete example.
It is frequent in mathematics
that every instance of a
concept of seemingly
great generality is
in essence the same as
a small and concrete
special case.”
— Paul Halmos in
I Want To Be a Mathematician
Euclid’s geometry deals with affine
spaces of 1, 2, and 3 dimensions
definable over the field
of real numbers.
Each of these spaces
has infinitely many points.
Some simpler spaces are those
defined over a finite field–
i.e., a “Galois” field–
for instance, the field
which has only two
elements, 0 and 1, with
addition and multiplication
as follows:
|
|

From these five finite spaces,
we may, in accordance with
Halmos’s advice,
select as “a small and
concrete special case”
the 4-point affine plane,
which we may call

Galois’s Window.
The interior lines of the picture
are by no means irrelevant to
the space’s structure, as may be
seen by examining the cases of
the above Galois affine 3-space
and Galois affine hyperplane
in greater detail.
For more on these cases, see
The Eightfold Cube,
Finite Relativity,
The Smallest Projective Space,
Latin-Square Geometry, and
Geometry of the 4×4 Square.
(These documents assume that
the reader is familar with the
distinction between affine and
projective geometry.)
These 8- and 16-point spaces
may be used to
illustrate the action of Klein’s
simple group of order 168
and the action of
a subgroup of 322,560 elements
within the large Mathieu group.
The view from Galois’s window
also includes aspects of
quantum information theory.
For links to some papers
in this area, see
Elements of Finite Geometry.

Professor Emeritus,
Institute for Advanced Study
Savage Logic
"Savage logic works like a kaleidoscope whose chips can fall into a variety of patterns while remaining unchanged in quantity, form, or color. The number of patterns producible in this way may be large if the chips are numerous and varied enough, but it is not infinite. The patterns consist in the disposition of the chips vis-a-vis one another (that is, they are a function of the relationships among the chips rather than their individual properties considered separately). And their range of possible transformations is strictly determined by the construction of the kaleidoscope, the inner law which governs its operation. And so it is too with savage thought. Both anecdotal and geometric, it builds coherent structures out of 'the odds and ends left over from psychological or historical process.'
These odds and ends, the chips of the kaleidoscope, are images drawn from myth, ritual, magic, and empirical lore. (How, precisely, they have come into being in the first place is one of the points on which Levi-Strauss is not too explicit, referring to them vaguely as the 'residue of events… fossil remains of the history of an individual or a society.') Such images are inevitably embodied in larger structures– in myths, ceremonies, folk taxonomies, and so on– for, as in a kaleidoscope, one always sees the chips distributed in some pattern, however ill-formed or irregular. But, as in a kaleidoscope, they are detachable from these structures and arrangeable into different ones of a similar sort. Quoting Franz Boas that 'it would seem that mythological worlds have been built up, only to be shattered again, and that new worlds were built from the fragments,' Levi-Strauss generalizes this permutational view of thinking to savage thought in general."
— Clifford Geertz, "The Cerebral Savage: the Structural Anthropology of Claude Levi-Strauss," in Encounter, Vol. 28 No. 4 (April 1967), pp. 25-32.
Today's New York Times
reports that
Geertz died on Monday,
October 30, 2006.
Related material:
and Up the River:
|
While it's a story that's never been written, a suggested title– Indiana Jones Sails Up The River Of Death–
shows how readily we as individuals or we as a culture can automatically visualize a basic story motif. We may each see the particular elements of the story differently, but almost instantaneously we catch its drift. The hero sails up the river of death to discover what lies within his own heart: i.e., how much moral and physical strength he has. Indiana Jones sails up the River of Death. We are following Indiana Jones up the River of Death. We're going to visit with Colonel Kurtz. (You may not want to get off the boat.) No, I am not mixing up metaphors. These are the Story. |
Amen.

Thanks to Peter Woit’s weblog
for a link to the above illustration.
This picture of
“Coxeter Exhuming Geometry”
suggests the following comparison:

For the second tombstone,
see this morning’s entry,
Birth, Death, and Symmetry.
Further details on the geometry
underlying the second tombstone:

The above is from
Variable Resolution 4–k Meshes:
Concepts and Applications (pdf),
by Luiz Velho and Jonas Gomes.
See also Symmetry Framed
and The Garden of Cyrus.
| “That corpse you planted last year in your garden, Has it begun to sprout? Will it bloom this year? Or has the sudden frost disturbed its bed?” — T. S. Eliot, “The Waste Land“ |
"O God, I could be bounded in a nutshell
and count myself a king of infinite space,
were it not that I have bad dreams."
— Hamlet
Background:
"… Something have you heard
Of Hamlet's transformation; so call it,
Sith nor the exterior nor the inward man
Resembles that it was…."
The transformation:
Click on picture for details.
Related material:
Figures of Speech (June 7, 2006) and
Ursprache Revisited (June 9, 2006).

— Opening sentence of
Martha Cooley’s The Archivist
“Frere Jacques, Cuernavaca,
ach du lieber August.”
— John O’Hara, Hope of Heaven, 1938
For Tom Stoppard on his birthday:
“For I remember when I began to read, and to take some pleasure in it, there was wont to lie in my mother’s parlour (I know not by what accident, for she herself never in her life read any book but of devotion), but there was wont to lie Spenser’s works; this I happened to fall upon, and was infinitely delighted with the stories of the knights, and giants, and monsters, and brave houses, which I found everywhere there (though my understanding had little to do with all this); and by degrees with the tinkling of the rhyme and dance of the numbers, so that I think I had read him all over before I was twelve years old, and was thus made a poet.”
Order and Ennui
Meanwhile, back at the Institute for Advanced Study:
May 25, 4:40 PM —
Research Seminar
(Simonyi Hall Seminar Room) —
Pirita Paajanen,
The Hebrew University of Jerusalem:
Zeta functions of
finitely generated infinite groups
Some background cited by Paajanen:
M.P.F. du Sautoy, “Zeta functions of groups: The quest for order versus the fl ight from ennui,” Groups St Andrews 2001 – in Oxford, Volume 1, CUP 2003.
Those who prefer the showbiz approach to mathematics (the flight from ennui?) may enjoy a website giving further background from du Sautoy.
|
Holy the Firm
by Annie Dillard Esoteric Christianity, I read, posits a substance. It is a created substance, lower than metals and minerals on a “spiritual scale” and lower than salts and earths, occurring beneath salts and earths in the waxy deepness of planets, but never on the surface of planets where men could discern it; and it is in touch with the Absolute, at base. In touch with the Absolute! At base. The name of this substance is Holy the Firm. These are only ideas, by the single handful. Lines, lines, and their infinite points! Hold hands and crack the whip, and yank the Absolute out of there and into the light, God pale and astounded, spraying a spiral of salts and earths, God footloose and flung. And cry down the line to his passing white ear, “Old Sir! Do you hold space from buckling by a finger in its hole? O Old! Where is your other hand?” His right hand is clenching, calm, round the exploding left hand of Holy the Firm. — Annie Dillard, Holy the Firm, Harper & Row 1977, reissued by Harper Perennial Library in 1988 as a paperback, pp. 68-71. |
From James A. Michener‘s The Source:
“Trouble started in a quarter that neither Uriel nor Zadok could have foreseen. For many generations the wiser men of Zadok’s clan had worshipped El-Shaddai with the understanding that whereas Canaanites and Egyptians could see their gods directly, El-Shaddai was invisible and inhabited no specific place. Unequivocally the Hebrew patriarchs had preached this concept and the sager men of the clans accepted it, but to the average Hebrew who was not a philosopher the theory of a god who lived nowhere, who did not even exist in corporeal form, was not easy to comprehend. Such people were willing to agree with Zadok that their god did not live on this mountain– the one directly ahead– but they suspected that he did live on some mountain nearby, and when they said this they pictured an elderly man with a white beard who lived in a proper tent and whom they might one day see and touch. If questioned, they would have said that they expected El-Shaddai to look much like their father Zadok, but with a longer beard, a stronger voice, and more penetrating eyes.
Now, as these simpler-minded Hebrews settled down outside the walls of Makor, they began to see Canaanite processions leave the main gate and climb the mountain to the north, seeking the high place where Baal lived, and they witnessed the joy which men experienced when visiting their god, and the Hebrews began in subtle ways and easy steps to evolve the idea that Baal, who obviously lived in a mountain, and El-Shaddai, who was reported to do so, must have much in common. Furtively at first, and then openly, they began to climb the footpath to the place of Baal, where they found a monolith rising from the highest point of rock. Here was a tangible thing they could comprehend, and after much searching along the face of the mountain, a group of Hebrew men found a straight rock of size equal to the one accorded Baal, and with much effort they dragged it one starless night to the mountain top, where they installed it not far from the home of Baal….”


The above monolith is perhaps more
closely related to El-Shaddai than to
Madonna, Grammy Night, and Baal.
It reflects my own interests
(Mathematics and Narrative)
and those of Martin Buber
(Jews on Fiction):

|
"…that ineffable constellation of talents that makes the player of rank: a gift for conceiving abstract schematic possibilities; a sense of mathematical poetry in the light of which the infinite chaos of probability and permutation is crystallized under the pressure of intense concentration into geometric blossoms; the ruthless focus of force on the subtlest weakness of an opponent."
— Trevanian,
Shibumi
'Even black has various subtle shades,' Sosuke nodded."
— Yasunari Kawabata,
The Old Capital
"The Zen disciple sits for long hours silent and motionless, with his eyes closed. Presently he enters a state of impassivity, free from all ideas and all thoughts. He departs from the self and enters the realm of nothingness. This is not the nothingness or the emptiness of the West. It is rather the reverse, a universe of the spirit in which everything communicates freely with everything, transcending bounds, limitless."
— Yasunari Kawabata,
Nobel lecture, 1968

Proof 101
From a course description:
“This module aims to introduce the student to rigorous university level mathematics….
Syllabus: The idea of and need for mathematical statements and proofs…. proof by contradiction… proof by induction…. the infinite number of primes….”
In the December Notices of the American Mathematical Society, Brian (E. B.) Davies, a professor of mathematics at King’s College London, questions the consistency of Peano Arithmetic (PA), which has the following axioms:
From BookRags.com—
Axiom 1. 0 is a number.
Axiom 2. The successor of any number is a number.
Axiom 3. If a and b are numbers and if their successors are equal, then a and b are equal.
Axiom 4. 0 is not the successor of any number.
Axiom 5. If S is a set of numbers containing 0 and if the successor of any number in S is also in S, then S contains all the numbers.
It should be noted that the word “number” as used in the Peano axioms means “non-negative integer.” The fifth axiom deserves special comment. It is the first formal statement of what we now call the “induction axiom” or “the principle of mathematical induction.”
Peano’s fifth axiom particularly troubles Davies, who writes elsewhere:
I contend that our understanding of number should be placed in an historical context, and that the number system is a human invention. Elementary arithmetic enables one to determine the number of primes less than twenty as certainly as anything we know. On the other hand Peano arithmetic is a formal system, and its internal consistency is not provable, except within set-theoretic contexts which essentially already assume it, in which case their consistency is also not provable. The proof that there exists an infinite number of primes does not depend upon counting, but upon the law of induction, which is an abstraction from our everyday experience….
… Geometry was a well developed mathematical discipline based upon explicit axioms over one and a half millennia before the law of induction was first formulated. Even today many university students who have been taught the principle of induction prefer to avoid its use, because they do not feel that it is as natural or as certain as a purely algebraic or geometric proof, if they can find one. The feelings of university students may not settle questions about what is truly fundamental, but they do give some insight into our native intuitions.— E. B. Davies in
“Counting in the real world,”
March 2003 (word format),
To appear in revised form in
Brit. J. Phil. Sci. as
“Some remarks on
the foundations
of quantum mechanics”
Exercise:
Discuss Davies’s claim that
The proof that there exists an infinite number of primes does not depend upon counting, but upon the law of induction.
Cite the following passage in your discussion.
It will be clear by now that, if we are to have any chance of making progress, I must produce examples of “real” mathematical theorems, theorems which every mathematician will admit to be first-rate.
… I can hardly do better than go back to the Greeks. I will state and prove two of the famous theorems of Greek mathematics. They are “simple” theorems, simple both in idea and in execution, but there is no doubt at all about their being theorems of the highest class. Each is as fresh and significant as when it was discovered– two thousand years have not written a wrinkle on either of them. Finally, both the statements and the proofs can be mastered in an hour by any intelligent reader, however slender his mathematical equipment.
I. The first is Euclid’s proof of the existence of an infinity of prime numbers.
The prime numbers or primes are the numbers
(A) 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …
which cannot be resolved into smaller factors. Thus 37 and 317 are prime. The primes are the material out of which all numbers are built up by multiplication: thus
666 = 2 . 3 . 3 . 37.
Every number which is not prime itself is divisible by at least one prime (usually, of course, by several). We have to prove that there are infinitely many primes, i.e. that the series (A) never comes to an end.
Let us suppose that it does, and that
2, 3, 5, . . . , P
is the complete series (so that P is the largest prime); and let us, on this hypothesis, consider the numberQ = (2 . 3 . 5 . . . . . P) + 1.
It is plain that Q is not divisible by any of
2, 3, 5, …, P;
for it leaves the remainder 1 when divided by any one of these numbers. But, if not itself prime, it is divisible by some prime, and therefore there is a prime (which may be Q itself) greater than any of them. This contradicts our hypothesis, that there is no prime greater than P; and therefore this hypothesis is false.
The proof is by reductio ad absurdum, and reductio ad absurdum, which Euclid loved so much, is one of a mathematician’s finest weapons. It is a far finer gambit than any chess gambit: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game.
— G. H. Hardy,
A Mathematician’s Apology,
quoted in the online guide for
Clear and Simple as the Truth:
Writing Classic Prose, by
Francis-Noël Thomas
and Mark Turner,
Princeton University Press
In discussing Davies’s claim that the above proof is by induction, you may want to refer to Davies’s statement that
Geometry was a well developed mathematical discipline based upon explicit axioms over one and a half millennia before the law of induction was first formulated
and to Hardy’s statement that the above proof is due to Euclid.
Hobgoblin?
Brian Davies is a professor of mathematics at King’s College London. In the December Notices of the American Mathematical Society, he claims that arithmetic may, for all we know, be inconsistent:
“It is not possible to prove that Peano arithmetic is consistent”…?!
Where did Gödel say this? Gödel proved, in fact, according to a well-known mathematician at Princeton, that (letting PA stand for Peano Arithmetic),
— Edward Nelson,
Mathematics and Faith (pdf)
Remarkably, even after he has stated correctly Gödel’s result, Nelson, like Davies, concludes that
I prefer the argument that the existence of a model ensures the consistency of a theory.
For instance, the Toronto philosopher William Seager writes that
The relationship between consistency and the existence of a model is brought home by the following weblog entry that neatly summarizes a fallacious argument offered in the AMS Notices by Davies:
Consider the following list A1 of axioms.
(1) There is a natural number 0.
(2) Every natural number a has a successor, denoted by S(a).
(3) There is no natural number whose successor is 0.
(4) Distinct natural numbers have distinct successors: a = b if and only if S(a) = S(b).
(5) If a property is possessed by 0 and also by the successor of every natural number which possesses it, then it is possessed by all the natural numbers.
Now consider the following list A2 of axioms.
(1) G is a set of elements and these elements obey the group axioms.
(2) G is finite but not isomorphic to any known list of finite simple groups.
(3) G is simple, in other words, if N is a subset of G satisfying certain properties then N=G.
We can roughly compare A2 with A1. The second axiom in A2 can be thought of as analogous to the third axiom of A1. Also the third axiom of A2 is analogous to the fifth axiom of A1, insofar as it refers to an unspecified set with cetain properties and concludes that it is equal to G.
Now, as is generally believed by most group theorists, the system A2 is internally inconsistent and the proof its inconsistency runs for more than 10000 pages.
So who is to deny that the system A1 is also probably internally inconsistent! Particularly since Godel proved that you can not prove it is consistent (staying inside the system). May be the shortest proof of its inconsistency is one hundred million pages long!
— Posted by Krishna,
11/29/2005 11:46:00 PM,
at his weblog,
“Quasi-Coherent Ruminations”
An important difference between A1 (the set of axioms of Peano arithmetic) and A2 (a set of axioms that describe a new, unknown, finite simple group) is that A1 is known to have a model (the nonnegative integers) and A2 is not known to have a model.
Therefore, according to Seager’s argument, A1 is consistent and A2 may or may not be consistent.
The degree to which Seager’s argument invokes Platonic realism is debatable. Less debatable is the quasireligious faith in nominalism proclaimed by Davies and Nelson. Nelson’s own account of a religious experience in 1976 at Toronto is instructive.
— Edward Nelson,
Mathematics and Faith (pdf)
Nelson’s “Mathematics and Faith” was written for the Jubilee for Men and Women from the World of Learning held at the Vatican, 23-24 May 2000. It concludes with an invocation of St. Paul:
— Edward Nelson,
Mathematics and Faith (pdf)
Belief in the consistency of arithmetic may or may not be foolish, and therefore an Emersonian hobgoblin of little minds, but bullshit is bullshit, whether in London, in Princeton, in Toronto, or in Rome.
Holy Geometry
What was “the holy geometry book” (“das heilige Geometrie-Büchlein,” p. 10 in the Schilpp book below) that so impressed the young Albert Einstein?
“At the age of 12 I experienced a second wonder of a totally different nature: in a little book dealing with Euclidian plane geometry, which came into my hands at the beginning of a schoolyear. Here were assertions, as for example the intersection of the three altitudes of a triangle in one point, which– though by no means evident– could nevertheless be proved with such certainty that any doubt appeared to be out of the question. This lucidity and certainty made an indescribable impression upon me.”
(“Im Alter von 12 Jahren erlebte ich ein zweites Wunder ganz verschiedener Art: An einem Büchlein über Euklidische Geometrie der Ebene, das ich am Anfang eines Schuljahres in die Hand bekam. Da waren Aussagen wie z.B. das Sich-Schneiden der drei Höhen eines Dreieckes in einem Punkt, die– obwohl an sich keineswegs evident– doch mit solcher Sicherheit bewiesen werden konnten, dass ein Zweifel ausgeschlossen zu sein schien. Diese Klarheit und Sicherheit machte einen unbeschreiblichen Eindruck auf mich.”)
— Albert Einstein, Autobiographical Notes, pages 8 and 9 in Albert Einstein: Philosopher-Scientist, ed. by Paul A. Schilpp
From a website by Hans-Josef Küpper:
“Today it cannot be said with certainty which book is Einstein’s ‘holy geometry book.’ There are three different titles that come into question:
Theodor Spieker, 1890
Lehrbuch der ebenen Geometrie. Mit Übungsaufgaben für höhere Lehranstalten.
Heinrich Borchert Lübsen, 1870
Ausführliches Lehrbuch der ebenen und sphärischen Trigonometrie. Zum Selbstunterricht. Mit Rücksicht auf die Zwecke des praktischen Lebens.
Adolf Sickenberger, 1888
Leitfaden der elementaren Mathematik.
Young Albert Einstein owned all of these three books. The book by T. Spieker was given to him by Max Talmud (later: Talmey), a Jewish medic. The book by H. B. Lübsen was from the library of his uncle Jakob Einstein and the one of A. Sickenberger was from his parents.”
Küpper does not state clearly his source for the geometry-book information.
According to Banesh Hoffman and Helen Dukas in Albert Einstein, Creator and Rebel, the holy geometry book was Lehrbuch der Geometrie zum Gebrauch an höheren Lehranstalten, by Eduard Heis (Catholic astronomer and textbook writer) and Thomas Joseph Eschweiler.
An argument for Sickenberger from The Young Einstein: The Advent of Relativity (pdf), by Lewis Pyenson, published by Adam Hilger Ltd., 1985:
“Throughout Einstein’s five and a half years at the Luitpold Gymnasium, he was taught mathematics from one or another edition of the separately published parts of Sickenberger’s Textbook of Elementary Mathematics. When it first appeared in 1888 the book constituted a major contribution to reform pedagogy. Sickenberger based his book on twenty years of experience that in his view necessarily took precedence over ‘theoretical doubts and systematic scruples.’ At the same time Sickenberger made much use of the recent pedagogical literature, especially that published in the pages of Immanuel Carl Volkmar Hoffmann’s Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht, the leading pedagogical mathematics journal of the day. Following in the tradition of the reform movement, he sought to present everything in the simplest, most intuitive way possible. He opposed introducing scientific rigour and higher approaches in an elementary text. He emphasised that he would follow neither the synthesis of Euclidean geometry nor the so-called analytical-genetic approach. He opted for a great deal of freedom in the form of presentation because he believed that a textbook was no more than a crutch for oral instruction. The spoken word, in Sickenberger’s view, could infuse life into the dead forms of the printed text. Too often, he insisted in the preface to his text, mathematics was seen and valued ‘as the pure science of reason.’ In reality, he continued, mathematics was also ‘an essential tool for daily work.’ In view of the practical dimension of mathematics Sickenberger sought most of all to present basic propositions clearly rather than to arrive at formal conciseness. Numerous examples took the place of long, complicated, and boring generalities. In addition to the usual rules of arithmetic Sickenberger introduced diophantine equations. To solve three linear, homogeneous, first-order equations with three unknowns he specified determinants and determinant algebra. Then he went on to quadratic equations and logarithms. In the second part of his book, Sickenberger treated plane geometry.
According to a biography of Einstein written by his step-son-in-law, Rudolf Kayser– one that the theoretical physicist described as ‘duly accurate’– when he was twelve years old Einstein fell into possession of the ‘small geometry book’ used in the Luitpold Gymnasium before this subject was formally presented to him. Einstein corroborated Kayser’s passage in autobiographical notes of 1949, when he described how at the age of twelve ‘a little book dealing with Euclidean plane geometry’ came into his hands ‘at the beginning of a school year.’ The ‘lucidity and certainty’ of plane geometry according to this ‘holy geometry booklet’ made, Einstein wrote, ‘an indescribable impression on me.’ Einstein saw here what he found in other texts that he enjoyed: it was ‘not too particular’ in logical rigour but ‘made up for this by permitting the main thoughts to stand out clearly and synoptically.’ Upon working his way through this text, Einstein was then presented with one of the many editions of Theodor Spieker’s geometry by Max Talmey, a medical student at the University of Munich who dined with the Einsteins and who was young Einstein’s friend when Einstein was between the ages of ten and fifteen. We can only infer from Einstein’s retrospective judgment that the first geometry book exerted an impact greater than that produced by Spieker’s treatment, by the popular science expositions of Aaron Bernstein and Ludwig Büchner also given to him by Talmey, or by the texts of Heinrich Borchert Lübsen from which Einstein had by the age of fourteen taught himself differential and integral calculus.
Which text constituted the ‘holy geometry booklet’? In his will Einstein gave ‘all his books’ to his long-time secretary Helen Dukas. Present in this collection are three bearing the signature ‘J Einstein’: a logarithmic and trigonometric handbook, a textbook on analysis, and an introduction to infinitesimal calculus. The signature is that of Einstein’s father’s brother Jakob, a business partner and member of Einstein’s household in Ulm and Munich. He presented the books to his nephew Albert. A fourth book in Miss Dukas’s collection, which does not bear Jakob Einstein’s name, is the second part of a textbook on geometry, a work of astronomer Eduard Heis’s which was rewritten after his death by the Cologne schoolteacher Thomas Joseph Eschweiler. Without offering reasons for his choice Banesh Hoffmann has recently identified Heis and Eschweiler’s text as the geometry book that made such an impression on Einstein. Yet, assuming that Kayser’s unambiguous reporting is correct, it is far more likely that the geometrical part of Sickenberger’s text was what Einstein referred to in his autobiographical notes. Sickenberger’s exposition was published seven years after that of Heis and Eschweiler, and unlike the latter it appeared with a Munich press. Because it was used in the Luitpold Gymnasium, copies would have been readily available to Uncle Jakob or to whoever first acquainted Einstein with Euclidean geometry.”
What might be the modern version of a “holy geometry book”?

Transcendence through spelling:
Richard Gere and Flora Cross
as father and daughter
in "Bee Season."
Words Made Flesh: Code, Culture, Imagination—
… letters create things by the virtue of an algorithm…
Spelling is a sign, Elly. When you win the national bee, we'll know that you are ready to follow in Abulafia's footsteps. Once you're able to let the letters guide you through any word you are given, you will be ready to receive shefa."
In the quiet of the room, the sound of Eliza and her father breathing is everything.
"Do you mean," Eliza whispers, "that I'll be able to talk to God?"

Diamond Theory notes
of Feb. 4, 1986,
of April 26, 1986, and
of May 26, 1986,
Sacerdotal Jargon
(Log24, Dec. 5, 2002),
and 720 in the Book
(Log24, Epiphany 2004).
“Do not underestimate Evil Cullinane’s plan for World Domination! http://www.log24.com now shows that he has crossed over to the dark side, making sacrifices to the Ancient Hindu Goddess ‘Kalli’ to ward off our attacks! ‘Kalli’-nane will soon appear as the top result on every Google search.

Soon, all young mathematicians will be hypnotised by his dark diamonds of falsehood. At least, that’s his plan. But wait, who’s that brilliant mathematician who shines the light right through Cullinane’s fraud and exposes him to the whole world?! Crankbuster saves the day! (applause)”
Related material:
“And if the band you’re in
starts playing different tunes
I’ll see you on
the dark side of the moon.”
“In Hindu mythology, Kali, the Divine Mother, is the symbol for the infinite diversity of experience. Kali represents the entire physical plane. She is the drama, tragedy, humor, and sorrow of life. She is the brother, father, sister, mother, lover, and friend. She is the fiend, monster, beast, and brute.”

“Tickle her under the chin
and she’ll stay with you forever.”
— People Weekly‘s “Hero Pets!”
July 14 1997
Dance
Yesterday’s AP “Thought for Today”–
“In some sort of crude sense which no vulgarity, no humor, no overstatement can quite extinguish, the physicists have known sin; and this is a knowledge which they cannot lose.” – J. Robert Oppenheimer, American physicist (1904-1967).
From Log24 on Dec. 17, 2002:
The Dancing Wu Li Masters,
by Gary Zukav, Harvard ’64:
“The Wu Li Masters know that physicists are doing more than ‘discovering the endless diversity of nature.’ They are dancing with Kali [or Durga], the Divine Mother of Hindu mythology.”
“Eastern religions have nothing to say about physics, but they have a great deal to say about human experience. In Hindu mythology, Kali, the Divine Mother, is the symbol for the infinite diversity of experience. Kali represents the entire physical plane. She is the drama, tragedy, humor, and sorrow of life. She is the brother, father, sister, mother, lover, and friend. She is the fiend, monster, beast, and brute. She is the sun and the ocean. She is the grass and the dew. She is our sense of accomplishment and our sense of doing worthwhile. Our thrill of discovery is a pendant on her bracelet. Our gratification is a spot of color on her cheek. Our sense of importance is the bell on her toe.
This full and seductive, terrible and wonderful earth mother always has something to offer. Hindus know the impossibility of seducing her or conquering her and the futility of loving her or hating her; so they do the only thing that they can do. They simply honor her.”
How could I dance with another….?
— John Lennon and Paul McCartney, 1962-1963
Mathematics and Metaphor
The current (June/July) issue of the Notices of the American Mathematical Society has two feature articles. The first, on the vulgarizer Martin Gardner, was dealt with here in a June 19 entry, Darkness Visible. The second is related to a letter of André Weil (pdf) that is in turn related to mathematician Barry Mazur’s attempt to rewrite mathematical history and to vulgarize other people’s research by using metaphors drawn, it would seem, from the Weil letter.
A Mathematical Lie conjectures that Mazur’s revising of history was motivated by a desire to dramatize some arcane mathematics, the Taniyama conjecture, that deals with elliptic curves and modular forms, two areas of mathematics that have been known since the nineteenth century to be closely related.
Mazur led author Simon Singh to believe that these two areas of mathematics were, before Taniyama’s conjecture of 1955, completely unrelated —
“Modular forms and elliptic equations live in completely different regions of the mathematical cosmos, and nobody would ever have believed that there was the remotest link between the two subjects.” — Simon Singh, Fermat’s Enigma, 1998 paperback, p. 182
This is false. See Robert P. Langlands, review of Elliptic Curves, by Anthony W. Knapp, Bulletin of the American Mathematical Society, January 1994.
It now appears that Mazur’s claim was in part motivated by a desire to emulate the great mathematician André Weil’s manner of speaking; Mazur parrots Weil’s “bridge” and “Rosetta stone” metaphors —
From Peter Woit’s weblog, Feb. 10, 2005:
“The focus of Weil’s letter is the analogy between number fields and the field of algebraic functions of a complex variable. He describes his ideas about studying this analogy using a third, intermediate subject, that of function fields over a finite field, which he thinks of as a ‘bridge‘ or ‘Rosetta stone.'”
In “A 1940 Letter of André Weil on Analogy in Mathematics,” (pdf), translated by Martin H. Krieger, Notices of the A.M.S., March 2005, Weil writes that
“The purely algebraic theory of algebraic functions in any arbitrary field of constants is not rich enough so that one might draw useful lessons from it. The ‘classical’ theory (that is, Riemannian) of algebraic functions over the field of constants of the complex numbers is infinitely richer; but on the one hand it is too much so, and in the mass of facts some real analogies become lost; and above all, it is too far from the theory of numbers. One would be totally obstructed if there were not a bridge between the two. And just as God defeats the devil: this bridge exists; it is the theory of the field of algebraic functions over a finite field of constants….
On the other hand, between the function fields and the ‘Riemannian’ fields, the distance is not so large that a patient study would not teach us the art of passing from one to the other, and to profit in the study of the first from knowledge acquired about the second, and of the extremely powerful means offered to us, in the study of the latter, from the integral calculus and the theory of analytic functions. That is not to say that at best all will be easy; but one ends up by learning to see something there, although it is still somewhat confused. Intuition makes much of it; I mean by this the faculty of seeing a connection between things that in appearance are completely different; it does not fail to lead us astray quite often. Be that as it may, my work consists in deciphering a trilingual text {[cf. the Rosetta Stone]}; of each of the three columns I have only disparate fragments; I have some ideas about each of the three languages: but I know as well there are great differences in meaning from one column to another, for which nothing has prepared me in advance. In the several years I have worked at it, I have found little pieces of the dictionary. Sometimes I worked on one column, sometimes under another.”
Here is another statement of the Rosetta-stone metaphor, from Weil’s translator, Martin H. Krieger, in the A.M.S. Notices of November 2004, “Some of What Mathematicians Do” (pdf):
“Weil refers to three columns, in analogy with the Rosetta Stone’s three languages and their arrangement, and the task is to ‘learn to read Riemannian.’ Given an ability to read one column, can you find its translation in the other columns? In the first column are Riemann’s transcendental results and, more generally, work in analysis and geometry. In the second column is algebra, say polynomials with coefficients in the complex numbers or in a finite field. And in the third column is arithmetic or number theory and combinatorial properties.”
For greater clarity, see Armand Borel (pdf) on Weil’s Rosetta stone, where the three columns are referred to as Riemannian (transcendental), Italian (“algebraico-geometric,” over finite fields), and arithmetic (i.e., number-theoretic).
From Fermat’s Enigma, by Simon Singh, Anchor paperback, Sept. 1998, pp. 190-191:
Barry Mazur: “On the one hand you have the elliptic world, and on the other you have the modular world. Both these branches of mathematics had been studied intensively but separately…. Than along comes the Taniyama-Shimura conjecture, which is the grand surmise that there’s a bridge between these two completely different worlds. Mathematicians love to build bridges.”
Simon Singh: “The value of mathematical bridges is enormous. They enable communities of mathematicians who have been living on separate islands to exchange ideas and explore each other’s creations…. The great potential of the Taniyama-Shimura conjecture was that it would connect two islands and allow them to speak to each other for the first time. Barry Mazur thinks of the Taniyama-Shimura conjecture as a translating device similar to the Rosetta stone…. ‘It’s as if you know one language and this Rosetta stone is going to give you an intense understanding of the other language,’ says Mazur. ‘But the Taniyama-Shimura conjecture is a Rosetta stone with a certain magical power.'”
If Mazur, who is scheduled to speak at a conference on Mathematics and Narrative this July, wants more material on stones with magical powers, he might consult The Blue Matrix and The Diamond Archetype.
|
Fade to Black “…that ineffable constellation of talents that makes the player of rank: a gift for conceiving abstract schematic possibilities; a sense of mathematical poetry in the light of which the infinite chaos of probability and permutation is crystallized under the pressure of intense concentration into geometric blossoms; the ruthless focus of force on the subtlest weakness of an opponent.” — Trevanian, Shibumi
“‘Haven’t there been splendidly elegant colors in Japan since ancient times?’ ‘Even black has various subtle shades,’ Sosuke nodded.” — Yasunari Kawabata, The Old Capital
An Ad Reinhardt painting
Ad Reinhardt, The viewer may need to tilt “The grid is a staircase to the Universal…. We could think about Ad Reinhardt, who, despite his repeated insistence that ‘Art is art,’ ended up by painting a series of… nine-square grids in which the motif that inescapably emerges is a Greek cross.  Greek Cross There is no painter in the West who can be unaware of the symbolic power of the cruciform shape and the Pandora’s box of spiritual reference that is opened once one uses it.” — Rosalind Krauss,
|
In memory of
St. William Golding
(Sept. 19, 1911 – June 19, 1993)
Cross-Referenced
From today’s New York Times,
a review of a Werner Herzog film,
“Wheel of Time,” that opens
today in Manhattan:
“With a little effort, anything can be
shown to connect with anything else:
existence is infinitely cross-referenced.”
— Opening sentence of
Martha Cooley’s The Archivist
These images suggest
a Google search on the phrase
“crucified on the wheel of time,”
From Dark City: A Hollywood Jesus Movie Review —
“There is something mesmerizing about this important film. It flows in the same vein as The Truman Show, The Game, and Pleasantville. Something isn’t real with the world around John Murdoch. Some group is trying to control things and it isn’t God.”
Amen.
Related material:
Skewed Mirrors and
The Graces of Paranoia
Powered by WordPress