Tuesday, April 7, 2020
Moonshine, the MOG, and the Hexacode
Friday, September 25, 2015
Friday, March 13, 2015
Mathieu Moonshine
(Continued from yesterday's "earlier references" link.)
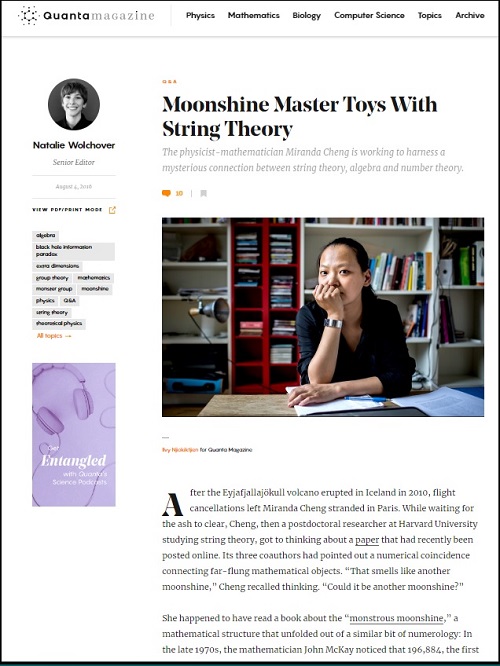
Yesterday at the Simons Foundation's Quanta Magazine :
See also earlier Log24 references to Mathieu moonshine .
I do not know the origin of this succinct phrase, taken from
an undated web page of Anne Taormina.
Friday, July 25, 2014
Magic in the Moonshine
“The yarns of seamen have a direct simplicity, the whole meaning
of which lies within the shell of a cracked nut. But Marlow was not
typical (if his propensity to spin yarns be excepted), and to him the
meaning of an episode was not inside like a kernel but outside,
enveloping the tale which brought it out only as a glow brings out a
haze, in the likeness of one of these misty halos that sometimes
are made visible by the spectral illumination of moonshine.”
— Joseph Conrad in Heart of Darkness
“By groping toward the light we are made to realize
how deep the darkness is around us.”
— Arthur Koestler, The Call Girls: A Tragi-Comedy,
Random House, 1973, page 118
“Spectral evidence is a form of evidence
based upon dreams and visions.” —Wikipedia
See also Moonshine (May 15, 2014) and, from the date of the above
New York Times item, two posts tagged Wunderkammer .
Related material: From the Spectrum program of the Mathematical
Association of America, some non-spectral evidence.
Thursday, May 15, 2014
Moonshine
“The yarns of seamen have a direct simplicity, the whole meaning
of which lies within the shell of a cracked nut. But Marlow was not
typical (if his propensity to spin yarns be excepted), and to him the
meaning of an episode was not inside like a kernel but outside,
enveloping the tale which brought it out only as a glow brings out a
haze, in the likeness of one of these misty halos that sometimes
are made visible by the spectral illumination of moonshine.”
— Joseph Conrad in Heart of Darkness
Photo of full moon over Oslo last night by Josefine Lyche:

A scene from my film viewing last night:

Some background (click to enlarge):
Note:
The “I, Frankenstein” scene above should not be interpreted as
a carrying of Martin Gardner through a lyche gate. Gardner
is, rather, symbolized by the asterisk in the first image from
the above Google search.
Thursday, September 5, 2013
Wednesday, September 4, 2013
Thursday, September 29, 2011
Michaelmas Moonshine
Lottery hermeneutics for Michaelmas—
New York Lottery the evening of Thursday, Sept. 29, 2011—
499 and 6985.
For 499, see post 499 in this journal ("Angel Night," Sept. 29, 2002).
For 6985, see a Sunday, 6/9/85, review of Amy's Eyes , a children's book by Richard Kennedy.
"Especially for the adult reader, the narrator's musings comprise many of the book's great pleasures. He discusses the seductiveness of numerology, the 'Wayward Daughter of Mathematics'….''
Wednesday, September 28, 2011
Mathieu Moonshine
The properties of the Mathieu group
For some related papers, see Mendeley.com.
Tuesday, December 12, 2023
If It’s Tuesday…

|
“The yarns of seamen have a direct simplicity, — Joseph Conrad in Heart of Darkness
“By groping toward the light we are made to realize
— Arthur Koestler, The Call Girls: A Tragi-Comedy, |
Saturday, April 29, 2023
Toying
From this journal on 4/01, 2009:
The Cruelest Month —

"Langdon sensed she was toying with him…." — Dan Brown
Less playfully . . .
See also the show tune from the end of "Second Tree from the Corner,"
a classic New Yorker short story by E. B. White. (And related posts.)
Saturday, January 29, 2022
Friday, October 8, 2021
Monday, April 19, 2021
Diamond Theorem at ScienceOpen
Update on April 20, 2021 —
The following was added today to the above summary:
“It describes a group of 322,560 permutations, later known as
‘the octad group,’ that now plays a role in speculative high-energy physics.
See Moonshine, Superconformal Symmetry, and Quantum Error Correction .”
Sunday, April 26, 2020
Crux
This post was suggested by a David Justice weblog post yesterday,
Coincidence and Cosmos. Some related remarks —
“The yarns of seamen have a direct simplicity, the whole meaning
of which lies within the shell of a cracked nut. But Marlow was not
typical (if his propensity to spin yarns be excepted), and to him the
meaning of an episode was not inside like a kernel but outside,
enveloping the tale which brought it out only as a glow brings out a
haze, in the likeness of one of these misty halos that sometimes
are made visible by the spectral illumination of moonshine.”
— Joseph Conrad in Heart of Darkness
“By groping toward the light we are made to realize
how deep the darkness is around us.”
— Arthur Koestler, The Call Girls: A Tragi-Comedy,
Random House, 1973, page 118
See as well posts now tagged Crux.
Saturday, March 7, 2020
The “Octad Group” as Symmetries of the 4×4 Square
From "Mathieu Moonshine and Symmetry Surfing" —
(Submitted on 29 Sep 2016, last revised 22 Jan 2018)
by Matthias R. Gaberdiel (1), Christoph A. Keller (2),
and Hynek Paul (1)
(1) Institute for Theoretical Physics, ETH Zurich
(2) Department of Mathematics, ETH Zurich
https://arxiv.org/abs/1609.09302v2 —
"This presentation of the symmetry groups Gi is
particularly well-adapted for the symmetry surfing
philosophy. In particular it is straightforward to
combine them into an overarching symmetry group G
by combining all the generators. The resulting group is
the so-called octad group
G = (Z2)4 ⋊ A8 .
It can be described as a maximal subgroup of M24
obtained by the setwise stabilizer of a particular
'reference octad' in the Golay code, which we take
to be O9 = {3,5,6,9,15,19,23,24} ∈ 𝒢24. The octad
subgroup is of order 322560, and its index in M24
is 759, which is precisely the number of
different reference octads one can choose."
This "octad group" is in fact the symmetry group of the affine 4-space over GF(2),
so described in 1979 in connection not with the Golay code but with the geometry
of the 4×4 square.* Its nature as an affine group acting on the Golay code was
known long before 1979, but its description as an affine group acting on
the 4×4 square may first have been published in connection with the
Cullinane diamond theorem and Abstract 79T-A37, "Symmetry invariance in a
diamond ring," by Steven H. Cullinane in Notices of the American Mathematical
Society , February 1979, pages A-193, 194.
* The Galois tesseract .
Update of March 15, 2020 —
Conway and Sloane on the "octad group" in 1993 —

Monday, July 15, 2019
Saturday, May 4, 2019
The Chinese Jars of Shing-Tung Yau
The title refers to Calabi-Yau spaces.
Four Quartets
. . . Only by the form, the pattern,
Can words or music reach
The stillness, as a Chinese jar still
Moves perpetually in its stillness.
A less "cosmic" but still noteworthy code — The Golay code.
This resides in a 12-dimensional space over GF(2).
Related material from Plato and R. T. Curtis —
A related Calabi-Yau "Chinese jar" first described in detail in 1905 —
A figure that may or may not be related to the 4x4x4 cube that
holds the classical Chinese "cosmic code" — the I Ching —

ftp://ftp.cs.indiana.edu/pub/hanson/forSha/AK3/old/K3-pix.pdf
Monday, April 23, 2018
Facets

See also the Feb. 17, 2017, post on Bertram Kostant
as well as "Mathieu Moonshine and Symmetry Surfing."
Wednesday, October 5, 2016
Sources
From a Google image search yesterday —

Sources (left to right, top to bottom) —
Math Guy (July 16, 2014)
The Galois Tesseract (Sept. 1, 2011)
The Full Force of Roman Law (April 21, 2014)
A Great Moonshine (Sept. 25, 2015)
A Point of Identity (August 8, 2016)
Pascal via Curtis (April 6, 2013)
Correspondences (August 6, 2011)
Symmetric Generation (Sept. 21, 2011)
Saturday, April 9, 2016
Expanding the Spielfeld (continued)
"Mr. Conrad was relentless and rigorous in expanding
the parameters of the fields in which he worked."
See also Spielfeld in this journal, as well as Conrad Moonshine.
Friday, April 1, 2016
Thursday, December 3, 2015
Overarching Symmetry
From p. 34 of the preprint "Snapshots of Conformal Field Theory,"
by Katrin Wendland, arXiv, 11 April 2014 —

50. Gannon, T.: Much ado about Mathieu (arXiv:1211.5531 [math.RT])
85. Taormina, A., Wendland, K.: The overarching finite symmetry group
of Kummer surfaces in the Mathieu group M24. JHEP 08, 125 (2013)
86. Taormina, A., Wendland, K.: Symmetry-surfing the moduli space
of Kummer K3s (arXiv:1303.2931 [hep-th])
87. Taormina, A., Wendland, K.: A twist in the M24 moonshine story
(arXiv:1303.3221 [hep-th])
The Wendland paper was published on Jan. 7, 2015, in
Mathematical Aspects of Quantum Field Theories ,
edited by Damien Calaque and Thomas Strobl
(Springer Mathematical Physics Studies), pages 89-129.
Friday, August 28, 2015
Sunday, May 17, 2015
Saturday, March 14, 2015
Introduction to Yau
This is related somewhat distantly to Mathieu moonshine.
Saturday, September 21, 2013
Mathematics and Narrative (continued)
Mathematics:
A review of posts from earlier this month —
Wednesday, September 4, 2013
|
Narrative:

Aooo.
Happy birthday to Stephen King.
Thursday, September 5, 2013
Kernel and Glow
"The yarns of seamen have a direct simplicity, the whole meaning
of which lies within the shell of a cracked nut. But Marlow was not
typical (if his propensity to spin yarns be excepted), and to him the
meaning of an episode was not inside like a kernel but outside,
enveloping the tale which brought it out only as a glow brings out a
haze, in the likeness of one of these misty halos that sometimes
are made visible by the spectral illumination of moonshine."
— Joseph Conrad in Heart of Darkness
Kernel — See Nocciolo.
Glow — See Moonshine and Moonshine II.
See also Cold Open (Jan. 29, 2011) and
Where Entertainment is God (Aug. 25, 2013).
Sunday, July 7, 2013
Mere 61
Today is the 61st anniversary of the publication
of the book Mere Christianity , by C. S. Lewis.
In its honor, here is a link to "Hexagram 61"
in this journal.
See also "Moonshine and Lion."
Monday, June 10, 2013
Galois Coordinates
Today's previous post on coordinate systems
suggests a look at the phrase "Galois coordinates."
A search shows that the phrase, though natural,
has apparently not been used before 2011* for solutions
to what Hermann Weyl called "the relativity problem."
A thorough historical essay on Galois coordinatization
in this sense would require more academic resources
than I have available. It would likely describe a number
of applications of Galois-field coordinates to square
(and perhaps to cubical) arrays that were studied before
1976, the date of my Diamond Theory monograph.
But such a survey might not find any such pre-1976
coordinatization of a 4×4 array by the 16 elements
of the vector 4-space over the Galois field with two
elements, GF(2).
Such coordinatizations are important because of their
close relationship to the Mathieu group M 24 .
See a preprint by Anne Taormina and Katrin Wendland,
"The overarching finite symmetry group of Kummer
surfaces in the Mathieu group M 24 ," with its remark
denying knowledge of any such coordinatization
prior to a 1989 paper by R. T. Curtis.
Related material:
Some images related to Galois coordinates, excerpted
from a Google search today (click to enlarge)—
* A rather abstract 2011 paper that uses the phrase
"Galois coordinates" may have some implications
for the naive form of the relativity problem
related to square and cubical arrays.
Saturday, May 11, 2013
Core
Promotional description of a new book:
“Like Gödel, Escher, Bach before it, Surfaces and Essences will profoundly enrich our understanding of our own minds. By plunging the reader into an extraordinary variety of colorful situations involving language, thought, and memory, by revealing bit by bit the constantly churning cognitive mechanisms normally completely hidden from view, and by discovering in them one central, invariant core— the incessant, unconscious quest for strong analogical links to past experiences— this book puts forth a radical and deeply surprising new vision of the act of thinking.”
“Like Gödel, Escher, Bach before it….”
Or like Metamagical Themas .
Rubik core:
Non- Rubik cores:
| Of the odd nxnxn cube: | Of the even nxnxn cube: |
Related material: The Eightfold Cube and…
“A core component in the construction
is a 3-dimensional vector space V over F2 .”
— Page 29 of “A twist in the M24 moonshine story,”
by Anne Taormina and Katrin Wendland.
(Submitted to the arXiv on 13 Mar 2013.)
Tuesday, April 30, 2013
Logline
Found this morning in a search:
A logline is a one-sentence summary of your script.
www.scriptologist.com/Magazine/Tips/Logline/logline.html
It's the short blurb in TV guides that tells you what a movie
is about and helps you decide if you're interested …
The search was suggested by a screenwriting weblog post,
"Loglines: WHAT are you doing?".
What is your story about?
No, seriously, WHAT are you writing about?
Who are the characters? What happens to them?
Where does it take place? What’s the theme?
What’s the style? There are nearly a million
little questions to answer when you set out
to tell a story. But it all starts with one
super, overarching question.
What are you writing about? This is the first
big idea that we pull out of the ether, sometimes
before we even have any characters.
What is your story about?
The screenwriting post was found in an earlier search for
the highlighted phrase.
The screenwriting post was dated December 15, 2009.
What I am doing now is checking for synchronicity.
This weblog on December 15, 2009, had a post
titled A Christmas Carol. That post referred to my 1976
monograph titled Diamond Theory .
I guess the script I'm summarizing right now is about
the heart of that theory, a group of 322,560 permutations
that preserve the symmetry of a family of graphic designs.
For that group in action, see the Diamond 16 Puzzle.
The "super overarching" phrase was used to describe
this same group in a different context:
This is from "Mathieu Moonshine," a webpage by Anne Taormina.
A logline summarizing my approach to that group:
Finite projective geometry explains
the surprising symmetry properties
of some simple graphic designs—
found, for instance, in quilts.
The story thus summarized is perhaps not destined for movie greatness.
Sunday, April 28, 2013
C’mon Baby…
 |
Let's do the twist. The image at left See this journal |
A phrase from yesterday's noon post:
Sinking the Magic 8-Ball .
A scene from the above film is related to this phrase.
Another image from the film poster:

A review of the film:
"The final 'twist' seems to negate the entire story,
like a bad shaggy-dog joke."
Such a joke:
“Words and numbers are of equal value,
for, in the cloak of knowledge,
one is warp and the other woof.”
— The princesses Rhyme and Reason
in The Phantom Tollbooth
"A core component in the construction
is a 3-dimensional vector space V over F2 ."
— Page 29 of "A twist in the M24 moonshine story,"
by Anne Taormina and Katrin Wendland.
(Submitted to the arXiv on 13 Mar 2013.)
The number of points in such a space is, of course, 8.
Saturday, April 27, 2013
Mark and Remark
“Fact and fiction weave in and out of novels like a shell game.” —R.B. Kitaj
Not just novels.
Fact:
The mark preceding A8 in the above denotes the semidirect product.
 |
Symbol from the box-style I Ching (Cullinane, 1/6/89). This is Hexagram 55, “Abundance [Fullness].” |
The mathematical quote, from last evening’s Symmetry, is from Anne Taormina.
The I Ching remark is not.
Another version of Abbondanza —
Fiction:
Found in Translation and the giorno June 22, 2009, here.
Friday, April 26, 2013
Symmetry
Anne Taormina on Mathieu Moonshine —
This is, of course, the same group (of order 322,560) underlying the Diamond 16 Puzzle.
The Cruelest Month continues…
"Well in North Carolina…" — George Jones
For those averse to white lightning —
A link in yesterday 's 5:24 PM post yields moonshine.
See also Title and 24 Hour Psycho.
Wednesday, October 31, 2012
Speak, Memory
"… the effective work of memory is the very definition of art."
— "In Memoriam: Chris Marker," by Richard Brody,
New Yorker weblog post, July 30, 2012
New York Lottery this evening: 178, 0772.
Definition: See 178 on May 25, 2012.
Art: See 772 on Nov. 21, 2010 and Harvard Black Diamond.
Moonshine:
The time of this post, 8:28, may be taken as
a reference to the date, 8/28, of the Feast of St. Augustine.
Augustine's remarks on memory are not without interest.
Wednesday, October 24, 2012
In a Nutshell
"The yarns of seamen have a direct simplicity,
the whole meaning of which
lies within the shell of a cracked nut.
But Marlow was not typical
(if his propensity to spin yarns be excepted),
and to him the meaning of an episode
was not inside like a kernel but outside,
enveloping the tale which brought it out
only as a glow brings out a haze,
in the likeness of one of these misty halos
that sometimes are made visible by
the spectral illumination of moonshine."
— Joseph Conrad in Heart of Darkness
Friday, December 23, 2011
Friday, June 24, 2011
Just One More Thing…
Moonshine and Lion
are left to bury the dead.
DEMETRIUS
Ay, and Wall too.
BOTTOM
[Starting up] No assure you;
the wall is down
that parted their fathers.
Click image for details.
Sunday, April 3, 2011
On to Chicago!
Commentary on last night—

Tonight: The After-Party.
In related news…

"The yarns of seamen have a direct simplicity, the whole meaning of which
lies within the shell of a cracked nut. But Marlow was not typical
(if his propensity to spin yarns be excepted), and to him the meaning
of an episode was not inside like a kernel but outside, enveloping the tale
which brought it out only as a glow brings out a haze, in the likeness of
one of these misty halos that sometimes are made visible by
the spectral illumination of moonshine."
– Joseph Conrad in Heart of Darkness , quoted here in
Cold Open (Saturday night, January 29, 2011)
Wednesday, March 2, 2011
Labyrinth of the Line
“Yo sé de un laberinto griego que es una línea única, recta.”
—Borges, “La Muerte y la Brújula”
“I know of one Greek labyrinth which is a single straight line.”
—Borges, “Death and the Compass”
Another single-line labyrinth—
Robert A. Wilson on the projective line with 24 points
and its image in the Miracle Octad Generator (MOG)—
Related material —
The remarks of Scott Carnahan at Math Overflow on October 25th, 2010
and the remarks at Log24 on that same date.
A search in the latter for miracle octad is updated below.

This search (here in a customized version) provides some context for the
Benedictine University discussion described here on February 25th and for
the number 759 mentioned rather cryptically in last night’s “Ariadne’s Clue.”
Update of March 3— For some historical background from 1931, see The Mathieu Relativity Problem.
Monday, February 7, 2011
Reappearing All Over Again
A sequel to "A Reappearing Number," "Reappearing Continued," and "Classical Requiem"—
A connection to the numerology of today's date, The Seventh— "Frame Tale." (Click, then scroll down.)
Saturday, January 29, 2011
Cold Open
"The yarns of seamen have a direct simplicity, the whole meaning of which lies within the shell of a cracked nut. But Marlow was not typical (if his propensity to spin yarns be excepted), and to him the meaning of an episode was not inside like a kernel but outside, enveloping the tale which brought it out only as a glow brings out a haze, in the likeness of one of these misty halos that sometimes are made visible by the spectral illumination of moonshine."
— Joseph Conrad in Heart of Darkness
Some background—

An image from yesterday's search
God, TIme, Hopkins
"We got tom-toms over here bigger than a monster
Bla Bla Bla Bla Bla Bla Bla Bla"
— "Massive Attack"
"I'm just checking your math on that. Yes, I got the same thing."
"Live… Uh, check that… From New York, it's Saturday Night! "
Saturday, August 2, 2008
Saturday August 2, 2008
Simon tells me he has a quasi-religious faith in the Monster. One day, he says, … the Monster will expose the structure of the universe.
… although Simon says he is keen for me to write a book about him and his work on the Monster and his obsession with buses, he doesn’t like talking, has no sense of anecdotes or extended conversation, and can’t remember (or never paid any attention to) 90 per cent of the things I want him to tell me about in his past. It is not modesty. Simon is not modest or immodest: he just has no self-curiosity. To Simon, Simon is a collection of disparate facts and no interpretative glue. He is a man without adjectives. His speech is made up almost entirely of short bursts of grunts and nouns.
This is the main reason why we spent three weeks together …. I needed to find a way to make him prattle.”
Those in search of prattle and interpretive glue should consult Anthony Judge’s essay ““Potential Psychosocial Significance of Monstrous Moonshine: An Exceptional Form of Symmetry as a Rosetta Stone for Cognitive Frameworks.” This was cited here in Thursday’s entry “Symmetry in Review.” (That entry is just a list of items related in part by synchronicity, in part by mathematical content. The list, while meaningful to me and perhaps a few others, is also lacking in prattle and interpretive glue.)
Those in search of knowledge, rather than glue and prattle, should consult Symmetry and the Monster, by Mark Ronan. If they have a good undergraduate education in mathematics, Terry Gannon‘s survey paper “Monstrous Moonshine: The First Twenty-Five Years” (pdf) and book– Moonshine Beyond the Monster— may also be of interest.
Thursday, July 31, 2008
Thursday July 31, 2008
“Put bluntly, who is kidding whom?”
— Anthony Judge, draft of
“Potential Psychosocial Significance
of Monstrous Moonshine:
An Exceptional Form of Symmetry
as a Rosetta Stone for
Cognitive Frameworks,”
dated September 6, 2007.
Good question.
Also from
September 6, 2007 —
the date of
Madeleine L’Engle‘s death —
 |
1. The performance of a work by
Richard Strauss,
“Death and Transfiguration,”
(Tod und Verklärung, Opus 24)
by the Chautauqua Symphony
at Chautauqua Institution on
July 24, 2008
2. Headline of a music review
in today’s New York Times:
Welcoming a Fresh Season of
Transformation and Death
3. The picture of the R. T. Curtis
Miracle Octad Generator
on the cover of the book
Twelve Sporadic Groups:

4. Freeman Dyson’s hope, quoted by
Gorenstein in 1986, Ronan in 2006,
and Judge in 2007, that the Monster
group is “built in some way into
the structure of the universe.”
5. Symmetry from Plato to
the Four-Color Conjecture
7. Yesterday’s entry,
“Theories of Everything“
Coda:

as a tesseract.“
— Madeleine L’Engle
For a profile of
L’Engle, click on
the Easter eggs.
Tuesday, January 6, 2004
Tuesday January 6, 2004
720 in the Book
Searching for an epiphany on this January 6 (the Feast of the Epiphany), I started with Harvard Magazine, the current issue of January-February 2004.
An article titled On Mathematical Imagination concludes by looking forward to
“a New Instauration that will bring mathematics, at last, into its rightful place in our lives: a source of elation….”
Seeking the source of the phrase “new instauration,” I found it was due to Francis Bacon, who “conceived his New Instauration as the fulfilment of a Biblical prophecy and a rediscovery of ‘the seal of God on things,’ ” according to a web page by Nieves Mathews.
Hmm.
The Mathews essay leads to Peter Pesic, who, it turns out, has written a book that brings us back to the subject of mathematics:
Abel’s Proof: An Essay
on the Sources and Meaning
of Mathematical Unsolvability
by Peter Pesic,
MIT Press, 2003
From a review:
“… the book is about the idea that polynomial equations in general cannot be solved exactly in radicals….
Pesic concludes his account after Abel and Galois… and notes briefly (p. 146) that following Abel, Jacobi, Hermite, Kronecker, and Brioschi, in 1870 Jordan proved that elliptic modular functions suffice to solve all polynomial equations. The reader is left with little clarity on this sequel to the story….”
— Roger B. Eggleton, corrected version of a review in Gazette Aust. Math. Soc., Vol. 30, No. 4, pp. 242-244
Here, it seems, is my epiphany:
“Elliptic modular functions suffice to solve all polynomial equations.”
Incidental Remarks
on Synchronicity,
Part I
Those who seek a star
on this Feast of the Epiphany
may click here.
Most mathematicians are (or should be) familiar with the work of Abel and Galois on the insolvability by radicals of quintic and higher-degree equations.
Just how such equations can be solved is a less familiar story. I knew that elliptic functions were involved in the general solution of a quintic (fifth degree) equation, but I was not aware that similar functions suffice to solve all polynomial equations.
The topic is of interest to me because, as my recent web page The Proof and the Lie indicates, I was deeply irritated by the way recent attempts to popularize mathematics have sown confusion about modular functions, and I therefore became interested in learning more about such functions. Modular functions are also distantly related, via the topic of “moonshine” and via the “Happy Family” of the Monster group and the Miracle Octad Generator of R. T. Curtis, to my own work on symmetries of 4×4 matrices.
Incidental Remarks
on Synchronicity,
Part II
There is no Log24 entry for
December 30, 2003,
the day John Gregory Dunne died,
but see this web page for that date.
Here is what I was able to find on the Web about Pesic’s claim:
From Wolfram Research:
From Solving the Quintic —
“Some of the ideas described here can be generalized to equations of higher degree. The basic ideas for solving the sextic using Klein’s approach to the quintic were worked out around 1900. For algebraic equations beyond the sextic, the roots can be expressed in terms of hypergeometric functions in several variables or in terms of Siegel modular functions.”
From Siegel Theta Function —
“Umemura has expressed the roots of an arbitrary polynomial in terms of Siegel theta functions. (Mumford, D. Part C in Tata Lectures on Theta. II. Jacobian Theta Functions and Differential Equations. Boston, MA: Birkhäuser, 1984.)”
From Polynomial —
“… the general quintic equation may be given in terms of the Jacobi theta functions, or hypergeometric functions in one variable. Hermite and Kronecker proved that higher order polynomials are not soluble in the same manner. Klein showed that the work of Hermite was implicit in the group properties of the icosahedron. Klein’s method of solving the quintic in terms of hypergeometric functions in one variable can be extended to the sextic, but for higher order polynomials, either hypergeometric functions in several variables or ‘Siegel functions’ must be used (Belardinelli 1960, King 1996, Chow 1999). In the 1880s, Poincaré created functions which give the solution to the nth order polynomial equation in finite form. These functions turned out to be ‘natural’ generalizations of the elliptic functions.”
Belardinelli, G. “Fonctions hypergéométriques de plusieurs variables er résolution analytique des équations algébrique générales.” Mémoral des Sci. Math. 145, 1960.
King, R. B. Beyond the Quartic Equation. Boston, MA: Birkhäuser, 1996.
Chow, T. Y. “What is a Closed-Form Number.” Amer. Math. Monthly 106, 440-448, 1999.
From Angel Zhivkov,
Preprint series,
Institut für Mathematik,
Humboldt-Universität zu Berlin:
“… discoveries of Abel and Galois had been followed by the also remarkable theorems of Hermite and Kronecker: in 1858 they independently proved that we can solve the algebraic equations of degree five by using an elliptic modular function…. Kronecker thought that the resolution of the equation of degree five would be a special case of a more general theorem which might exist. This hypothesis was realized in [a] few cases by F. Klein… Jordan… showed that any algebraic equation is solvable by modular functions. In 1984 Umemura realized the Kronecker idea in his appendix to Mumford’s book… deducing from a formula of Thomae… a root of [an] arbitrary algebraic equation by Siegel modular forms.”
— “Resolution of Degree Less-than-or-equal-to Six Algebraic Equations by Genus Two Theta Constants“
Incidental Remarks
on Synchronicity,
Part III
From Music for Dunne’s Wake:
“Heaven was kind of a hat on the universe,
a lid that kept everything underneath it
where it belonged.”
— Carrie Fisher,
Postcards from the Edge
|
“720 in |
“The group Sp4(F2) has order 720,”
as does S6. — Angel Zhivkov, op. cit.
Those seeking
“a rediscovery of
‘the seal of God on things,’ “
as quoted by Mathews above,
should see
The Unity of Mathematics
and the related note
Sacerdotal Jargon.

For more remarks on synchronicity
that may or may not be relevant
to Harvard Magazine and to
the annual Joint Mathematics Meetings
that start tomorrow in Phoenix, see
For the relevance of the time
of this entry, 10:10, see
|
Related recreational reading:
|
Labyrinth |
|
Monday, April 28, 2003
Monday April 28, 2003
ART WARS:
Toward Eternity
April is Poetry Month, according to the Academy of American Poets. It is also Mathematics Awareness Month, funded by the National Security Agency; this year's theme is "Mathematics and Art."
Some previous journal entries for this month seem to be summarized by Emily Dickinson's remarks:
"Because I could not stop for Death–
He kindly stopped for me–
The Carriage held but just Ourselves–
And Immortality.
Since then–'tis Centuries–and yet
Feels shorter than the Day
I first surmised the Horses' Heads
Were toward Eternity– "
|
Math Awareness Month April is Math Awareness Month.
|
|
An Offer He Couldn't Refuse Today's birthday: Francis Ford Coppola is 64.
From a note on geometry of April 28, 1985:
|
|
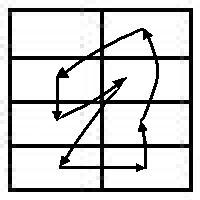
The Eight Today, the fourth day of the fourth month, plays an important part in Katherine Neville's The Eight. Let us honor this work, perhaps the greatest bad novel of the twentieth century, by reflecting on some properties of the number eight. Consider eight rectangular cells arranged in an array of four rows and two columns. Let us label these cells with coordinates, then apply a permutation.
The resulting set of arrows that indicate the movement of cells in a permutation (known as a Singer 7-cycle) outlines rather neatly, in view of the chess theme of The Eight, a knight. This makes as much sense as anything in Neville's fiction, and has the merit of being based on fact. It also, albeit rather crudely, illustrates the "Mathematics and Art" theme of this year's Mathematics Awareness Month. The visual appearance of the "knight" permutation is less important than the fact that it leads to a construction (due to R. T. Curtis) of the Mathieu group M24 (via the Curtis Miracle Octad Generator), which in turn leads logically to the Monster group and to related "moonshine" investigations in the theory of modular functions. See also "Pieces of Eight," by Robert L. Griess. |
Friday, April 4, 2003
Friday April 4, 2003
The Eight
Today, the fourth day of the fourth month, plays an important part in Katherine Neville's The Eight. Let us honor this work, perhaps the greatest bad novel of the twentieth century, by reflecting on some properties of the number eight. Consider eight rectangular cells arranged in an array of four rows and two columns. Let us label these cells with coordinates, then apply a permutation.
|
|
|
|
|
The resulting set of arrows that indicate the movement of cells in a permutation (known as a Singer 7-cycle) outlines rather neatly, in view of the chess theme of The Eight, a knight. This makes as much sense as anything in Neville's fiction, and has the merit of being based on fact. It also, albeit rather crudely, illustrates the "Mathematics and Art" theme of this year's Mathematics Awareness Month. (See the 4:36 PM entry.)
The visual appearance of the "knight" permutation is less important than the fact that it leads to a construction (due to R. T. Curtis) of the Mathieu group M24 (via the Curtis Miracle Octad Generator), which in turn leads logically to the Monster group and to related "moonshine" investigations in the theory of modular functions. See also "Pieces of Eight," by Robert L. Griess.