Related art by Basquiat —
Click on the above image for an Instagram description of its source.
See also related artistic remarks in this journal on the date of that
Instagram description — October 17, 2022.
Sunday, December 3, 2023
Red Skull and the Tesseract Box
Comments Off on Red Skull and the Tesseract Box
Saturday, October 24, 2020
The Galois Tesseract
Stanley E. Payne and J. A. Thas in 1983* (previous post) —
“… a 4×4 grid together with
the affine lines on it is AG(2,4).”
Payne and Thas of course use their own definition
of affine lines on a grid.
Actually, a 4×4 grid together with the affine lines on it
is, viewed in a different way, not AG(2,4) but rather AG(4,2).
For AG(4,2) in the proper context, see
Affine Groups on Small Binary Spaces and
The Galois Tesseract.
* And 26 years later, in 2009.
Comments Off on The Galois Tesseract
Monday, October 15, 2018
Monday, March 12, 2018
“Quantum Tesseract Theorem?”
Remarks related to a recent film and a not-so-recent film.
For some historical background, see Dirac and Geometry in this journal.
Also (as Thas mentions) after Saniga and Planat —
The Saniga-Planat paper was submitted on December 21, 2006.
Excerpts from this journal on that date —
"Open the pod bay doors, HAL."
Comments Off on “Quantum Tesseract Theorem?”
Saturday, May 20, 2017
van Lint and Wilson Meet the Galois Tesseract*
Click image to enlarge.
The above 35 projective lines, within a 4×4 array —
The above 15 projective planes, within a 4×4 array (in white) —
* See Galois Tesseract in this journal.
Comments Off on van Lint and Wilson Meet the Galois Tesseract*
Thursday, May 11, 2017
Reopening the Tesseract
Dialogue from the film "Interstellar" —
Cooper: Did it work?
TARS: I think it might have.
Cooper: How do you know?
TARS: Because the bulk beings
are closing the tesseract.
Related material — "Bulk apperception"
in this journal, and …
Comments Off on Reopening the Tesseract
Wednesday, December 28, 2016
Rosetta Tesseracts
Comments Off on Rosetta Tesseracts
Tuesday, March 24, 2015
Brouwer on the Galois Tesseract
Yesterday's post suggests a review of the following —
|
Andries Brouwer, preprint, 1982:
"The Witt designs, Golay codes and Mathieu groups" Pages 8-9: Substructures of S(5, 8, 24) An octad is a block of S(5, 8, 24). Theorem 5.1
Let B0 be a fixed octad. The 30 octads disjoint from B0
the design of the points and affine hyperplanes in AG(4, 2), Proof…. … (iv) We have AG(4, 2).
(Proof: invoke your favorite characterization of AG(4, 2) An explicit construction of the vector space is also easy….) |
Related material: Posts tagged Priority.
Comments Off on Brouwer on the Galois Tesseract
Tuesday, December 10, 2013
Wittgenstein’s Tesseract
See also last night's "Pink Champagne on Ice" post.
The "ice" in that post's title refers to the white lines
forming a tesseract in the book cover's background—
"icy white and crystalline," as Johnny Mercer put it.
(A Tune for Josefine, Nov. 25.)
See also the tag Diamond Theory tesseract in this journal.
Comments Off on Wittgenstein’s Tesseract
Saturday, July 6, 2013
The People’s Tesseract*
From Andries Brouwer —
* Related material: Yesterday's evening post and The People's Cube.
(By the way, any 4×4 array is a tesseract .)
Comments Off on The People’s Tesseract*
Thursday, August 16, 2012
Raiders of the Lost Tesseract
(Continued from August 13. See also Coxeter Graveyard.)
Here the tombstone says
"GEOMETRY… 600 BC — 1900 AD… R.I.P."
In the geometry of Plato illustrated below,
"the figure of eight [square] feet" is not , at this point
in the dialogue, the diamond in Jowett's picture.
An 1892 figure by Jowett illustrating Plato's Meno—
Jowett's picture is nonetheless of interest for
its resemblance to a figure drawn some decades later
by the Toronto geometer H. S. M. Coxeter.
A similar 1950 figure by Coxeter illustrating a tesseract—
For a less scholarly, but equally confusing, view of the number 8,
see The Eight , a novel by Katherine Neville.
Comments Off on Raiders of the Lost Tesseract
Monday, August 13, 2012
Raiders of the Lost Tesseract
(An episode of Mathematics and Narrative )
A report on the August 9th opening of Sondheim's Into the Woods—
Amy Adams… explained why she decided to take on the role of the Baker’s Wife.
“It’s the ‘Be careful what you wish’ part,” she said. “Since having a child, I’m really aware that we’re all under a social responsibility to understand the consequences of our actions.” —Amanda Gordon at businessweek.com
Related material—
Amy Adams in Sunshine Cleaning "quickly learns the rules and ropes of her unlikely new market. (For instance, there are products out there specially formulated for cleaning up a 'decomp.')" —David Savage at Cinema Retro
Compare and contrast…
1. The following item from Walpurgisnacht 2012—
2. The six partitions of a tesseract's 16 vertices
into four parallel faces in Diamond Theory in 1937—
Comments Off on Raiders of the Lost Tesseract
Sunday, July 29, 2012
The Galois Tesseract
The three parts of the figure in today's earlier post "Defining Form"—
— share the same vector-space structure:
| 0 | c | d | c + d |
| a | a + c | a + d | a + c + d |
| b | b + c | b + d | b + c + d |
| a + b | a + b + c | a + b + d | a + b + c + d |
(This vector-space a b c d diagram is from Chapter 11 of
Sphere Packings, Lattices and Groups , by John Horton
Conway and N. J. A. Sloane, first published by Springer
in 1988.)
The fact that any 4×4 array embodies such a structure was implicit in
the diamond theorem (February 1979). Any 4×4 array, regarded as
a model of the finite geometry AG(4, 2), may be called a Galois tesseract.
(So called because of the Galois geometry involved, and because the
16 cells of a 4×4 array with opposite edges identified have the same
adjacency pattern as the 16 vertices of a tesseract (see, for instance,
Coxeter's 1950 "Self-Dual Configurations and Regular Graphs," figures
5 and 6).)
A 1982 discussion of a more abstract form of AG(4, 2):
Source:
The above 1982 remarks by Brouwer may or may not have influenced
the drawing of the above 1988 Conway-Sloane diagram.
Comments Off on The Galois Tesseract
Monday, June 4, 2012
Cube to Tesseract
Yesterday's post Child's Play displayed a cube formed
by a Hasse diagram of the 8 subsets of a 3-set.*
This suggests a review of a post from last January—
* See a comment on yesterday's post relating it to earlier,
very similar, remarks by Margaret Masterman.
I was unaware yesterday that those remarks exist.
Comments Off on Cube to Tesseract
Tuesday, January 31, 2012
Tesseract
|
"… a finite set with n elements Tesseract formed from a 4-set—
The same 16 subsets or points can
"There is such a thing as a 4-set." |
Update of August 12, 2012:
Figures like the above, with adjacent vertices differing in only one coordinate,
appear in a 1950 paper of H. S. M. Coxeter—
Comments Off on Tesseract
Saturday, September 3, 2011
The Galois Tesseract (continued)
A post of September 1, The Galois Tesseract, noted that the interplay
of algebraic and geometric properties within the 4×4 array that forms
two-thirds of the Curtis Miracle Octad Generator (MOG) may first have
been described by Cullinane (AMS abstract 79T-A37, Notices , Feb. 1979).
Here is some supporting material—
The passage from Carmichael above emphasizes the importance of
the 4×4 square within the MOG.
The passage from Conway and Sloane, in a book whose first edition
was published in 1988, makes explicit the structure of the MOG's
4×4 square as the affine 4-space over the 2-element Galois field.
The passage from Curtis (1974, published in 1976) describes 35 sets
of four "special tetrads" within the 4×4 square of the MOG. These
correspond to the 35 sets of four parallel 4-point affine planes within
the square. Curtis, however, in 1976 makes no mention of the affine
structure, characterizing his 140 "special tetrads" rather by the parity
of their intersections with the square's rows and columns.
The affine structure appears in the 1979 abstract mentioned above—
The "35 structures" of the abstract were listed, with an application to
Latin-square orthogonality, in a note from December 1978—
See also a 1987 article by R. T. Curtis—
Further elementary techniques using the miracle octad generator, by R. T. Curtis. Abstract:
“In this paper we describe various techniques, some of which are already used by devotees of the art, which relate certain maximal subgroups of the Mathieu group M24, as seen in the MOG, to matrix groups over finite fields. We hope to bring out the wealth of algebraic structure* underlying the device and to enable the reader to move freely between these matrices and permutations. Perhaps the MOG was mis-named as simply an ‘octad generator’; in this paper we intend to show that it is in reality a natural diagram of the binary Golay code.”
(Received July 20 1987)
– Proceedings of the Edinburgh Mathematical Society (Series 2) (1989), 32: 345-353
* For instance:
Update of Sept. 4— This post is now a page at finitegeometry.org.
Comments Off on The Galois Tesseract (continued)
Thursday, September 1, 2011
Wednesday, August 7, 2024
Purely Coincidental Spatial Studies
See also the previous post.
Update of 1 (and 1:35) PM EDT the same day —
Some Spatial Studies vocabulary: http://m759.net/wordpress/?s=Dyadic.
Comments Off on Purely Coincidental Spatial Studies
Tuesday, April 23, 2024
Golden Keys
“Chess problems are the
hymn-tunes of mathematics.”
— G. H. Hardy,
A Mathematician’s Apology
|
|
“The key is the cocktail that begins the proceedings.”
– Brian Harley, Mate in Two Moves
"I named this script ocode and chmod 755'd it to make it executable…"
— Software forum post on the OCR program Tesseract
|
From the author of
The Pearly Gates of Cyberspace:
"Like so many other heroes
who have seen the light
of a higher order…."
Comments Off on Golden Keys
Monday, January 22, 2024
Box Geometry
From a search in this journal for "Box of Nothing" —
"And the Führer digs for trinkets in the desert."
From a related search, for "Ghent Links" —
Related art —
More seriously… See Box759.
Comments Off on Box Geometry
Monday, January 15, 2024
Foursquare Variations
From Encyclopedia of Mathematics —
The above images from the history of mathematics might be
useful at some future point for illustrating academic hurly-burly.
Related reading . . .
Comments Off on Foursquare Variations
Saturday, November 18, 2023
“Don’t solicit for your sister,* it’s not nice.” — Tom Lehrer
From this journal at 1:51 AM ET Thursday, September 8, 2022 —
"The pleasure comes from the illusion" . . .
Exercise:
Compare and contrast the following structure with the three
"bricks" of the R. T. Curtis Miracle Octad Generator (MOG).
Note that the 4-row-2-column "brick" at left is quite
different from the other two bricks, which together
show chevron variations within a Galois tesseract —
.
Further Weil remarks . . .
A Slew of Prayers
"The pleasure comes from the illusion
and the far from clear meaning;
once the illusion is dissipated,
and knowledge obtained, one becomes
indifferent at the same time;
at least in the Gitâ there is a slew of prayers
(slokas) on the subject, each one more final
than the previous ones."
* —
Comments Off on “Don’t solicit for your sister,* it’s not nice.” — Tom Lehrer
Tuesday, October 3, 2023
Tuesday… Belgium.
The inscape in the previous post suggests a review of
work by the Belgian mathematician Koen Thas on what
might be called the "quantum tesseract theorem."
Comments Off on Tuesday… Belgium.
Friday, July 28, 2023
Requiem for an Eagle
" 'Hotel California,' with its mysterious, allegorical lyrics,
became among the band’s best-known recordings.
It topped the Billboard Hot 100 in 1977 and won
a Grammy Award for record of the year in 1978."
— The New York Times tonight on an Eagles founding
member who reportedly died on Wednesday, July 26.
"Mirrors on the ceiling, pink champagne on ice . . . ."
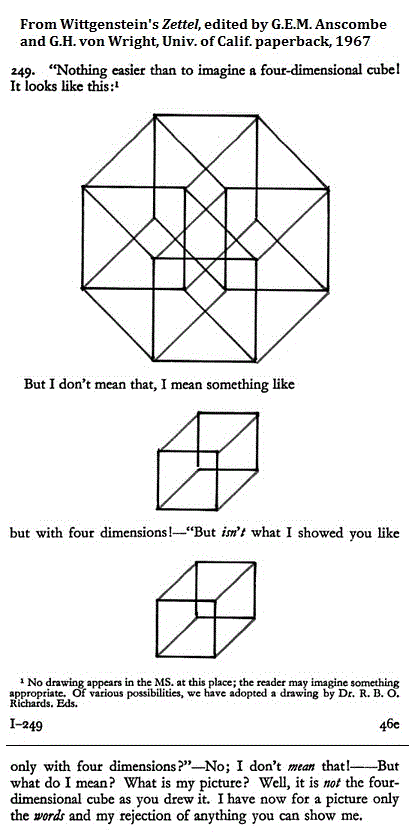
See as well a search in this journal for Zettel .
Comments Off on Requiem for an Eagle
Monday, June 19, 2023
The Original Portable Door
"… a cardboard tube, more or less the same length as
the inner core of a toilet roll, but thicker. He frowned,
took the roll out, laid it on the desk and poked up it
with the butt end of a pencil. Something slid out.
It looked like a rolled-up black plastic dustbin liner;
but when he unfolded it, he recognised it as the funny
sheet thing he’d found in the strongroom and briefly
described as an Acme Portable Door, before losing
his nerve and changing it to something less facetious."
— Holt, Tom. The Portable Door . Orbit. Kindle Edition.
According to goodreads.com, the Holt book was
"first published March 6, 2003."
Compare and contrast the "portable door" as a literary device
with the "tesseract" in A Wrinkle in Time (1962).
See also this journal on March 6, 2003.
Comments Off on The Original Portable Door
Friday, April 28, 2023
The Small Space Model
From the previous post, "The Large Language Model,"
a passage from Wikipedia —
"… sometimes large models undergo a 'discontinuous phase shift'
where the model suddenly acquires substantial abilities not seen
in smaller models. These are known as 'emergent abilities,' and
have been the subject of substantial study." — Wikipedia
Compare and contrast
this with the change undergone by a "small space model,"
that of the finite affine 4-space A with 16 points (a Galois tesseract ),
when it is augmented by an eight-point "octad." The 30 eight-point
hyperplanes of A then have a natural extension within the new
24-point set to 759 eight-point octads, and the 322,560 affine
automorphisms of the space expand to the 244,823,040 Mathieu
automorphisms of the 759-octad set — a (5, 8, 24) Steiner system.
For a visual analogue of the enlarged 24-point space and some remarks
on analogy by Simone Weil's brother, a mathematician, see this journal
on September 8 and 9, 2022.
Comments Off on The Small Space Model
Saturday, April 1, 2023
For this weekend’s Bombay Beach Biennale
Comments Off on For this weekend’s Bombay Beach Biennale
Tuesday, March 28, 2023
Onestone Parable
“You’re literally looking for like a one in a million thing.
You filter out the 999,999 of the boring ones, then
you’ve got something that’s weird, and then that’s worth
further exploration.”
— Quote from a mathematics story today at Gizmodo
A different "one in a million" mathematics story —
On Steiner Quadruple Systems of Order 16.
See also Galois Tesseract.
Comments Off on Onestone Parable
Sunday, February 19, 2023
Hoarding Space
Comments Off on Hoarding Space
Friday, January 13, 2023
Dürer, Music, and Doktor Faustus
The previous post and Mann's Doktor Faustus in this journal
suggest a look at . . .
Comments Off on Dürer, Music, and Doktor Faustus
Thursday, December 22, 2022
Thursday, November 24, 2022
The Drum Machine
"A struggling music producer sells his soul to a 1970s drum machine."
— Summary of a short film by Kevin Ignatius, "Hook Man."
The music producer pawns his current drum device
and acquires a demonic 1970s machine.
Artistic symbolism —
The 16-pad device at left may be viewed by enthusiasts of ekphrasis
as a Galois tesseract, and the machine at right as the voice of
Hal Foster, an art theorist who graduated from Princeton in 1977.
For an example of Foster's prose style, see
the current London Review of Books.
Comments Off on The Drum Machine
Friday, November 18, 2022
Datura Date
There was no Log24 post for the above Jacky Klein date,
July 6, 2016, but the posts of that month contain a flashback
to an earlier July 6 —
See as well . . .
… and some Log24 posts from the above Dec. 1, 2014, date
now tagged Red Dawn.
Comments Off on Datura Date
Monday, November 14, 2022
Plot Structure
From Peter J. Cameron's weblog today —
"It happens sometimes that researchers working in different fields
study the same thing, give it different names, and don’t realise that
there is further work on the subject somewhere else…."
Cameron's example of a theorem connecting work on
the same thing in different fields —
"Theorem A partition Δ is equitable for a graph Γ if and only if
the projection matrix onto the subspace of functions constant
on parts of Δ commutes with the adjacency matrix of Γ."
A phrase from Cameron's remarks today —
"Thus we have to consider 'plot structure'…."
For more remarks on different fields and plot structure , see
"Quantum Tesseract Theorem" in this weblog.
Comments Off on Plot Structure
Saturday, October 15, 2022
A Box of Nothing . . .
Comments Off on A Box of Nothing . . .
Sunday, September 25, 2022
Woodwork
"The actor Nick Offerman, himself an accomplished woodworker
and a member of Ms. Hiller’s legion of admirers, called her an
'Obi-Wan Kenobi level master.'"
— The New York Times this evening, obituary by Clay Risen
for Nancy Hiller.
Related woodwork note —
Comments Off on Woodwork
Thursday, September 8, 2022
Analogy in Mathematics: Chevron Variations
André Weil in 1940 on analogy in mathematics —
| . "Once it is possible to translate any particular proof from one theory to another, then the analogy has ceased to be productive for this purpose; it would cease to be at all productive if at one point we had a meaningful and natural way of deriving both theories from a single one. In this sense, around 1820, mathematicians (Gauss, Abel, Galois, Jacobi) permitted themselves, with anguish and delight, to be guided by the analogy between the division of the circle (Gauss’s problem) and the division of elliptic functions. Today, we can easily show that both problems have a place in the theory of abelian equations; we have the theory (I am speaking of a purely algebraic theory, so it is not a matter of number theory in this case) of abelian extensions. Gone is the analogy: gone are the two theories, their conflicts and their delicious reciprocal reflections, their furtive caresses, their inexplicable quarrels; alas, all is just one theory, whose majestic beauty can no longer excite us. Nothing is more fecund than these slightly adulterous relationships; nothing gives greater pleasure to the connoisseur, whether he participates in it, or even if he is an historian contemplating it retrospectively, accompanied, nevertheless, by a touch of melancholy. The pleasure comes from the illusion and the far from clear meaning; once the illusion is dissipated, and knowledge obtained, one becomes indifferent at the same time; at least in the Gitâ there is a slew of prayers (slokas) on the subject, each one more final than the previous ones." |
"The pleasure comes from the illusion" . . .
Exercise:
Compare and contrast the following structure with the three
"bricks" of the R. T. Curtis Miracle Octad Generator (MOG).
Note that the 4-row-2-column "brick" at left is quite
different from the other two bricks, which together
show chevron variations within a Galois tesseract —
Comments Off on Analogy in Mathematics: Chevron Variations
Saturday, September 3, 2022
1984 Revisited
Note the three quadruplets of parallel edges in the 1984 figure above.
The above Gates article appeared earlier, in the June 2010 issue of
Physics World , with bigger illustrations. For instance —
Exercise: Describe, without seeing the rest of the article,
the rule used for connecting the balls above.
Wikipedia offers a much clearer picture of a (non-adinkra) tesseract —
And then, more simply, there is the Galois tesseract —
For parts of my own world in June 2010, see this journal for that month.
The above Galois tesseract appears there as follows:
See also the Klein correspondence in a paper from 1968
in yesterday's 2:54 PM ET post.
Comments Off on 1984 Revisited
Tuesday, August 23, 2022
Wednesday, August 3, 2022
From the “Shifting Phantasmagoria” of Joan Didion
Also on July 30 . . .
Comments Off on From the “Shifting Phantasmagoria” of Joan Didion
Saturday, July 30, 2022
Literary Figures
"… the tesseract, identified with a figure too inclusive,
contradictory, and all-pervasive to be seen as a character,
connects multiple dimensions in a manner counter to
ordinary thought…."
— Catherine Flynn, "From Dowel to Tesseract" (2016)
Comments Off on Literary Figures
Summer Camp
Or: The Sontag Puzzlement
Wikipedia on "Heavenly Creatures" —
"Juliet introduces Pauline to the idea of 'the Fourth World',
a Heaven without Christians where music and art are
celebrated. Juliet believes she will go there when she dies.
Certain actors and musicians have the status of saints in
this afterlife, such as singer Mario Lanza, with whom
both girls are obsessed."
Related material — Sontag + Camp .
Comments Off on Summer Camp
Saturday, March 26, 2022
Box Geometry: Space, Group, Art (Work in Progress)
| Name Tag | .Space | .Group | .Art |
|---|---|---|---|
| Box4 |
2×2 square representing the four-point finite affine geometry AG(2,2). (Box4.space) |
S4 = AGL(2,2) (Box4.group) |
(Box4.art) |
| Box6 |
3×2 (3-row, 2-column) rectangular array representing the elements of an arbitrary 6-set. |
S6 | |
| Box8 | 2x2x2 cube or 4×2 (4-row, 2-column) array. | S8 or A8 or AGL(3,2) of order 1344, or GL(3,2) of order 168 | |
| Box9 | The 3×3 square. | AGL(2,3) or GL(2,3) | |
| Box12 | The 12 edges of a cube, or a 4×3 array for picturing the actions of the Mathieu group M12. | Symmetries of the cube or elements of the group M12 | |
| Box13 | The 13 symmetry axes of the cube. | Symmetries of the cube. | |
| Box15 |
The 15 points of PG(3,2), the projective geometry of 3 dimensions over the 2-element Galois field. |
Collineations of PG(3,2) | |
| Box16 |
The 16 points of AG(4,2), the affine geometry of 4 dimensions over the 2-element Galois field. |
AGL(4,2), the affine group of |
|
| Box20 | The configuration representing Desargues's theorem. | ||
| Box21 | The 21 points and 21 lines of PG(2,4). | ||
| Box24 | The 24 points of the Steiner system S(5, 8, 24). | ||
| Box25 | A 5×5 array representing PG(2,5). | ||
| Box27 |
The 3-dimensional Galois affine space over the 3-element Galois field GF(3). |
||
| Box28 | The 28 bitangents of a plane quartic curve. | ||
| Box32 |
Pair of 4×4 arrays representing orthogonal Latin squares. |
Used to represent elements of AGL(4,2) |
|
| Box35 |
A 5-row-by-7-column array representing the 35 lines in the finite projective space PG(3,2) |
PGL(3,2), order 20,160 | |
| Box36 | Eurler's 36-officer problem. | ||
| Box45 | The 45 Pascal points of the Pascal configuration. | ||
| Box48 | The 48 elements of the group AGL(2,3). | AGL(2,3). | |
| Box56 |
The 56 three-sets within an 8-set or |
||
| Box60 | The Klein configuration. | ||
| Box64 | Solomon's cube. |
— Steven H. Cullinane, March 26-27, 2022
Comments Off on Box Geometry: Space, Group, Art (Work in Progress)
Tuesday, March 15, 2022
Midnight Wrinkle
See as well the life of a real astrophysicist.
Update of 12:26 PM ET March 15:
Vide other posts now tagged The Rosenhain Symmetry.
Comments Off on Midnight Wrinkle
Monday, February 21, 2022
Stimulus
"The class is objectively characterized, but not
the individual coordinate assignment."
Tell it to Watchduck, Hermann.
See a related remark by Quack5quack in Raiders of the Lost Coordinates.
Comments Off on Stimulus
Sunday, February 20, 2022
4×4 Nomenclature
The geometry of the 4×4 square may be associated with the name
Galois, as in "the Galois tesseract," or similarly with the name Kummer.
Here is a Google image search using the latter name —
(Click to enlarge.)
Comments Off on 4×4 Nomenclature
Thursday, February 17, 2022
Four Dots, Six Lines
"There is such a thing as a tesseract."
— Mrs. Whatsit in A Wrinkle in Time (1962)
"Simplify, simplify." — Henry David Thoreau in Walden (1854)
|
A Jungian on this six-line figure:
“They are the same six lines that exist in the I Ching…. Now observe the square more closely: four of the lines are of equal length, the other two are longer…. For this reason symmetry cannot be statically produced and a dance results.” |
Comments Off on Four Dots, Six Lines
Tuesday, December 21, 2021
Grid Language, Grid Logic
Comments Off on Grid Language, Grid Logic
Friday, December 10, 2021
Unhinged Melody
The time of the previous post was 4:46 AM ET today.
Fourteen minutes later —
"I'm a groupie, really." — Murray Bartlett in today's online NY Times
The previous post discussed group actions on a 3×3 square array. A tune
about related group actions on a 4×4 square array (a Galois tesseract ) . . .
Comments Off on Unhinged Melody
Sunday, December 5, 2021
Saturday, December 4, 2021
Delphic Code
Log24 on this date — December 4th — in 2008:
"I named this script ocode and chmod 755'd it to make it executable…"
— Software forum post on the OCR program Tesseract
The New York Times at 7:55 PM ET today:
Comments Off on Delphic Code
Sunday, April 11, 2021
Space Itself
See the title in this journal. This review was suggested by
a phrase of Catherine Flynn:
Comments Off on Space Itself
Saturday, April 10, 2021
Gap Dance in Utrecht
(See also Gap Dance elsewhere in this journal.)
"… the Wake seemed to be everywhere
at the Utrecht Joyce Symposium."
"What I saw at the Symposium at Utrecht
were scholars working to close the gap
between the multifaceted complexity
of the text and the vastly greater complexity
of the readers experiencing it."
— "Along the Krommerun: The Twenty-Fourth International
James Joyce Symposium, Utrecht, The Netherlands,
15-20 June 2014," by Andrew Ferguson, University of Virginia.
|
"Central to these structural and aesthetic innovations, however, is a mundane element: the wooden dowel. The dowel is a small peg of variable length; its ends lack distinct heads, allowing it work in any direction. The dowels remain hidden in the Red Blue Chair as they connect rail to rail and rail to plank, invisible yet essential to the chair's appearance and its defiance of convention and gravity. Critics have noted the chair's flouting of the rules of modern architectural semantics: Yves-Alain Bois writes of the elements that function simultaneously in two ways, as both supporting prop and supported cantilever, as subverting "the functionalist ethic of modernist architecture — the dictum that would have one meaning per sign". It is the dowel that allows the elements of the chair to attain so subtly this semantic complexity. The chair's innovations are not technological, but rather concern the arrangement and deployment of existing materials and elements. The dowel is a modest but highly adaptable means of joining: while the dovetail joint requires two equally sized components, the mortise and tenon involves a male and a female element, and the housed joint requires an extended zone of contact, the dowel neutrally connects all kinds of elements to one another, its single point allowing maximum freedom in the orientation of the connected elements." — Page 25 of "From Dowel to Tesseract," |
Comments Off on Gap Dance in Utrecht
Wednesday, February 17, 2021
Raiders of the Lost Coordinates . . .
From other posts tagged Tetrahedron vs. Square —
"There is such a thing as a 4-set."
— Saying adapted from a 1962 young-adult novel.
Illustration (central detail a from the above tetrahedral figure) —
A Harvard Variation
from Timothy Leary —
The topics of Harvard and Leary suggest some other cultural
history, from The Coasters — "Poison Ivy" and "Yakety Yak."
Comments Off on Raiders of the Lost Coordinates . . .
Wednesday, November 18, 2020
La Chanson Fatale
Harold Edwards, a founding co-editor of The Mathematical Intelligencer ,
reportedly died at 84 on Tuesday, Nov. 10, 2020.
Images from this journal on that date —
"Surprise Party" revisited —
A Philippine meditation by Alex Garland quoted here on May 6, 2010 —
Comments Off on La Chanson Fatale
Monday, July 13, 2020
Unpoetic License
The above novel uses extensively the term “inscape.”
The term’s originator, a 19th-century Jesuit poet,
is credited . . . sort of. For other uses of the term,
search for Inscape in this journal. From that search —
A quote from a 1962 novel —
“There’s something phoney
in the whole setup, Meg thought.
There is definitely something rotten
in the state of Camazotz.”
Addendum for the Church of Synchronology —
The Joe Hill novel above was published (in hardcover)
on Walpurgisnacht —April 30, 2013. See also this journal
on that date.
Comments Off on Unpoetic License
Tuesday, April 21, 2020
Living Water
The Tesseract Timeline:
Where The Cube Has Been In The …
www.cinemablend.com › news › the-tesseract-timeline-…
Mar 13, 2019 – With HYDRA. In 1942, Johann Schmidt, a.k.a.
the Red Skull, arrived in Tønsberg to procure the Tesseract
from an ancient church. While he …
Related material from posts tagged Aqua
(suggested by a name in the previous post) —
Comments Off on Living Water
Saturday, March 7, 2020
The “Octad Group” as Symmetries of the 4×4 Square
From "Mathieu Moonshine and Symmetry Surfing" —
(Submitted on 29 Sep 2016, last revised 22 Jan 2018)
by Matthias R. Gaberdiel (1), Christoph A. Keller (2),
and Hynek Paul (1)
(1) Institute for Theoretical Physics, ETH Zurich
(2) Department of Mathematics, ETH Zurich
https://arxiv.org/abs/1609.09302v2 —
"This presentation of the symmetry groups Gi is
particularly well-adapted for the symmetry surfing
philosophy. In particular it is straightforward to
combine them into an overarching symmetry group G
by combining all the generators. The resulting group is
the so-called octad group
G = (Z2)4 ⋊ A8 .
It can be described as a maximal subgroup of M24
obtained by the setwise stabilizer of a particular
'reference octad' in the Golay code, which we take
to be O9 = {3,5,6,9,15,19,23,24} ∈ 𝒢24. The octad
subgroup is of order 322560, and its index in M24
is 759, which is precisely the number of
different reference octads one can choose."
This "octad group" is in fact the symmetry group of the affine 4-space over GF(2),
so described in 1979 in connection not with the Golay code but with the geometry
of the 4×4 square.* Its nature as an affine group acting on the Golay code was
known long before 1979, but its description as an affine group acting on
the 4×4 square may first have been published in connection with the
Cullinane diamond theorem and Abstract 79T-A37, "Symmetry invariance in a
diamond ring," by Steven H. Cullinane in Notices of the American Mathematical
Society , February 1979, pages A-193, 194.
* The Galois tesseract .
Update of March 15, 2020 —
Conway and Sloane on the "octad group" in 1993 —
Comments Off on The “Octad Group” as Symmetries of the 4×4 Square
Monday, February 24, 2020
Hidden Figure
Comments Off on Hidden Figure
Tuesday, January 28, 2020
Very Stable Kool-Aid
Two of the thumbnail previews
from yesterday's 1 AM post …
Further down in the "6 Prescott St." post, the link 5 Divinity Avenue
leads to …
|
A Letter from Timothy Leary, Ph.D., July 17, 1961
Harvard University July 17, 1961
Dr. Thomas S. Szasz Dear Dr. Szasz: Your book arrived several days ago. I've spent eight hours on it and realize the task (and joy) of reading it has just begun. The Myth of Mental Illness is the most important book in the history of psychiatry. I know it is rash and premature to make this earlier judgment. I reserve the right later to revise and perhaps suggest it is the most important book published in the twentieth century. It is great in so many ways–scholarship, clinical insight, political savvy, common sense, historical sweep, human concern– and most of all for its compassionate, shattering honesty. . . . . |
The small Morton Prince House in the above letter might, according to
the above-quoted remarks by Corinna S. Rohse, be called a "jewel box."
Harvard moved it in 1978 from Divinity Avenue to its current location at
6 Prescott Street.
Related "jewel box" material for those who
prefer narrative to mathematics —
"In The Electric Kool-Aid Acid Test , Tom Wolfe writes about encountering
'a young psychologist,' 'Clifton Fadiman’s nephew, it turned out,' in the
waiting room of the San Mateo County jail. Fadiman and his wife were
'happily stuffing three I-Ching coins into some interminable dense volume*
of Oriental mysticism' that they planned to give Ken Kesey, the Prankster-
in-Chief whom the FBI had just nabbed after eight months on the lam.
Wolfe had been granted an interview with Kesey, and they wanted him to
tell their friend about the hidden coins. During this difficult time, they
explained, Kesey needed oracular advice."
— Tim Doody in The Morning News web 'zine on July 26, 2012**
Oracular advice related to yesterday evening's
"jewel box" post …
A 4-dimensional hypercube H (a tesseract ) has 24 square
2-dimensional faces. In its incarnation as a Galois tesseract
(a 4×4 square array of points for which the appropriate transformations
are those of the affine 4-space over the finite (i.e., Galois) two-element
field GF(2)), the 24 faces transform into 140 4-point "facets." The Galois
version of H has a group of 322,560 automorphisms. Therefore, by the
orbit-stabilizer theorem, each of the 140 facets of the Galois version has
a stabilizer group of 2,304 affine transformations.
Similar remarks apply to the I Ching In its incarnation as
a Galois hexaract , for which the symmetry group — the group of
affine transformations of the 6-dimensional affine space over GF(2) —
has not 322,560 elements, but rather 1,290,157,424,640.
* The volume Wolfe mentions was, according to Fadiman, the I Ching.
** See also this journal on that date — July 26, 2012.
Comments Off on Very Stable Kool-Aid
Monday, January 27, 2020
Jewel Box
The phrase "jewel box" in a New York Times obituary online this afternoon
suggests a review. See "And He Built a Crooked House" and Galois Tesseract.
Comments Off on Jewel Box
Monday, October 21, 2019
Algebra and Space… Illustrated.
Related entertainment —
Detail:
George Steiner —
"Perhaps an insane conceit."
Perhaps.
See Quantum Tesseract Theorem .
Perhaps Not.
See Dirac and Geometry .
Comments Off on Algebra and Space… Illustrated.
Tuesday, October 15, 2019
Inside the Fire Temple
(The title refers to Log24 posts now tagged Fire Temple.)
In memory of a New Yorker cartoonist who
reportedly died at 97 on October 3, 2019 …
"Read something that means something."
— New Yorker advertising slogan
From posts tagged Tetrahedron vs. Square —
This journal on October 3 —
"There is such a thing as a 4-set."
— Saying adapted from a 1962 young-adult novel.
Illustration (central detail a from the above tetrahedral figure) —
Comments Off on Inside the Fire Temple
Wednesday, October 9, 2019
The Joy of Six
Note that in the pictures below of the 15 two-subsets of a six-set,
the symbols 1 through 6 in Hudson's square array of 1905 occupy the
same positions as the anticommuting Dirac matrices in Arfken's 1985
square array. Similarly occupying these positions are the skew lines
within a generalized quadrangle (a line complex) inside PG(3,2).
Related narrative — The "Quantum Tesseract Theorem."
Comments Off on The Joy of Six
Sunday, September 22, 2019
Simplex Sigillum Veri
(Continued from November 27, 2010.)
The previous post suggests a review of a Tilman Piesk
illustration, with the general form of a 4-simplex, from
the Wikipedia article titled Simplex . As the article
notes, the lines shown connecting points are those of a
tesseract.
Comments Off on Simplex Sigillum Veri
Wednesday, September 18, 2019
The Perpetual Identity Crisis
"There is such a thing as a 4-set." — Saying adapted
from a 1962 young-adult novel.
Midrash — An image posted here on August 6 —
Comments Off on The Perpetual Identity Crisis
Tuesday, August 6, 2019
Mathematics and Narrative: The Crosswicks Curse Continues.
"There is such a thing as a desktop."
— Saying adapted from a 1962 young-adult novel.
Comments Off on Mathematics and Narrative: The Crosswicks Curse Continues.
Sunday, July 14, 2019
Old Pathways in Science:
The Quantum Tesseract Theorem Revisited
"The secret is that the super-mathematician expresses by the anticommutation
of his operators the property which the geometer conceives as perpendicularity
of displacements. That is why on p. 269 we singled out a pentad of anticommuting
operators, foreseeing that they would have an immediate application in describing
the property of perpendicular directions without using the traditional picture of space.
They express the property of perpendicularity without the picture of perpendicularity.
Thus far we have touched only the fringe of the structure of our set of sixteen E-operators.
Only by entering deeply into the theory of electrons could I show the whole structure
coming into evidence."
A related illustration, from posts tagged Dirac and Geometry —
Compare and contrast Eddington's use of the word "perpendicular"
with a later use of the word by Saniga and Planat.
Comments Off on Old Pathways in Science:
Tuesday, July 9, 2019
Perception of Space
The three previous posts have now been tagged . . .
Tetrahedron vs. Square and Triangle vs. Cube.
Related material —
Tetrahedron vs. Square:
Labeling the Tetrahedral Model (Click to enlarge) —
Triangle vs. Cube:
… and, from the date of the above John Baez remark —
Comments Off on Perception of Space
Monday, July 8, 2019
Exploring Schoolgirl Space
See also "Quantum Tesseract Theorem" and "The Crosswicks Curse."
Comments Off on Exploring Schoolgirl Space
Thursday, July 4, 2019
From Devil’s Night 2014
And now, General, time presses; and America is in a hurry.
Have you realized that though you may occupy towns and win battles,
you cannot conquer a nation? — The Devil's Disciple
A figure related to Dürer's "magic" square posted during Devil's Night —
Comments Off on From Devil’s Night 2014
Tuesday, April 9, 2019
Zero Dark Nine:
The Crosswicks Curse Continues . . .
"There is such a thing as geometry."
— Saying adapted from a 1962 young-adult novel.
Comments Off on Zero Dark Nine:
Monday, March 11, 2019
Ant-Man Meets Doctor Strange
The 4×4 square may also be called the Galois Tesseract .
By analogy, the 4x4x4 cube may be called the Galois Hexeract .
Comments Off on Ant-Man Meets Doctor Strange
Overarching Metanarratives
See also "Overarching + Tesseract" in this journal. From the results
of that search, some context for the "inscape" of the previous post —
Comments Off on Overarching Metanarratives
Wednesday, March 6, 2019
The Relativity Problem and Burkard Polster
|
From some 1949 remarks of Weyl— "The relativity problem is one of central significance throughout geometry and algebra and has been recognized as such by the mathematicians at an early time." — Hermann Weyl, "Relativity Theory as a Stimulus in Mathematical Research," Proceedings of the American Philosophical Society , Vol. 93, No. 7, Theory of Relativity in Contemporary Science: Papers Read at the Celebration of the Seventieth Birthday of Professor Albert Einstein in Princeton, March 19, 1949 (Dec. 30, 1949), pp. 535-541 Weyl in 1946—: "This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them." — Hermann Weyl, The Classical Groups , Princeton University Press, 1946, p. 16 |
For some context, see Relativity Problem in this journal.
In the case of PG(3,2), there is a choice of geometric models
to be coordinatized: two such models are the traditional
tetrahedral model long promoted by Burkard Polster, and
the square model of Steven H. Cullinane.
The above Wikipedia section tacitly (and unfairly) assumes that
the model being coordinatized is the tetrahedral model. For
coordinatization of the square model, see (for instance) the webpage
Finite Relativity.
For comparison of the two models, see a figure posted here on
May 21, 2014 —
Labeling the Tetrahedral Model (Click to enlarge) —
"Citation needed" —
The anonymous characters who often update the PG(3,2) Wikipedia article
probably would not consider my post of 2014, titled "The Tetrahedral
Model of PG(3,2)," a "reliable source."
Comments Off on The Relativity Problem and Burkard Polster
Thursday, February 28, 2019
Wikipedia Scholarship
Besides omitting the name Cullinane, the anonymous Wikipedia author
also omitted the step of representing the hypercube by a 4×4 array —
an array called in this journal a Galois tesseract.
Comments Off on Wikipedia Scholarship
Sunday, February 17, 2019
See Also …
"And the Führer digs for trinkets in the desert."
"See also Acht "
— Cambridge German-English Dictionary, article on "Elf "
Comments Off on See Also …
Wednesday, December 12, 2018
An Inscape for Douthat
Some images, and a definition, suggested by my remarks here last night
on Apollo and Ross Douthat's remarks today on "The Return of Paganism" —
In finite geometry and combinatorics,
an inscape is a 4×4 array of square figures,
each figure picturing a subset of the overall 4×4 array:
Related material — the phrase
"Quantum Tesseract Theorem" and …
A. An image from the recent
film "A Wrinkle in Time" —
B. A quote from the 1962 book —
"There's something phoney
in the whole setup, Meg thought.
There is definitely something rotten
in the state of Camazotz."
Comments Off on An Inscape for Douthat
Tuesday, November 13, 2018
Blackboard Jungle Continues.
From the 1955 film "Blackboard Jungle" —
From a trailer for the recent film version of A Wrinkle in Time —
Detail of the phrase "quantum tesseract theorem":
From the 1962 book —
"There's something phoney
in the whole setup, Meg thought.
There is definitely something rotten
in the state of Camazotz."
Related mathematics from Koen Thas that some might call a
"quantum tesseract theorem" —
Some background —
See also posts tagged Dirac and Geometry. For more
background on finite geometry, see a web page
at Thas's institution, Ghent University.
Comments Off on Blackboard Jungle Continues.
Monday, October 15, 2018
History at Bellevue
The previous post, "Tesserae for a Tesseract," contains the following
passage from a 1987 review of a book about Finnegans Wake —
"Basically, Mr. Bishop sees the text from above
and as a whole — less as a sequential story than
as a box of pied type or tesserae for a mosaic,
materials for a pattern to be made."
A set of 16 of the Wechsler cubes below are tesserae that
may be used to make patterns in the Galois tesseract.
Another Bellevue story —
“History, Stephen said, is a nightmare
from which I am trying to awake.”
— James Joyce, Ulysses
Comments Off on History at Bellevue
Tuesday, September 4, 2018
MBTI at the Church of St. Frank*
Comments Off on MBTI at the Church of St. Frank*
Wednesday, June 27, 2018
Taken In
A passage that may or may not have influenced Madeleine L'Engle's
writings about the tesseract :
|
From Mere Christianity , by C. S. Lewis (1952) —
"Book IV – Beyond Personality: I warned you that Theology is practical. The whole purpose for which we exist is to be thus taken into the life of God. Wrong ideas about what that life is, will make it harder. And now, for a few minutes, I must ask you to follow rather carefully. You know that in space you can move in three ways—to left or right, backwards or forwards, up or down. Every direction is either one of these three or a compromise between them. They are called the three Dimensions. Now notice this. If you are using only one dimension, you could draw only a straight line. If you are using two, you could draw a figure: say, a square. And a square is made up of four straight lines. Now a step further. If you have three dimensions, you can then build what we call a solid body, say, a cube—a thing like a dice or a lump of sugar. And a cube is made up of six squares. Do you see the point? A world of one dimension would be a straight line. In a two-dimensional world, you still get straight lines, but many lines make one figure. In a three-dimensional world, you still get figures but many figures make one solid body. In other words, as you advance to more real and more complicated levels, you do not leave behind you the things you found on the simpler levels: you still have them, but combined in new ways—in ways you could not imagine if you knew only the simpler levels. Now the Christian account of God involves just the same principle. The human level is a simple and rather empty level. On the human level one person is one being, and any two persons are two separate beings—just as, in two dimensions (say on a flat sheet of paper) one square is one figure, and any two squares are two separate figures. On the Divine level you still find personalities; but up there you find them combined in new ways which we, who do not live on that level, cannot imagine. In God's dimension, so to speak, you find a being who is three Persons while remaining one Being, just as a cube is six squares while remaining one cube. Of course we cannot fully conceive a Being like that: just as, if we were so made that we perceived only two dimensions in space we could never properly imagine a cube. But we can get a sort of faint notion of it. And when we do, we are then, for the first time in our lives, getting some positive idea, however faint, of something super-personal—something more than a person. It is something we could never have guessed, and yet, once we have been told, one almost feels one ought to have been able to guess it because it fits in so well with all the things we know already. You may ask, "If we cannot imagine a three-personal Being, what is the good of talking about Him?" Well, there isn't any good talking about Him. The thing that matters is being actually drawn into that three-personal life, and that may begin any time —tonight, if you like. . . . . |
But beware of being drawn into the personal life of the Happy Family .
https://www.jstor.org/stable/24966339 —
"The colorful story of this undertaking begins with a bang."
And ends with …
"Galois was a thoroughly obnoxious nerd,
suffering from what today would be called
a 'personality disorder.' His anger was
paranoid and unremitting."
Comments Off on Taken In
Thursday, June 21, 2018
Models of Being
A Buddhist view —
“Just fancy a scale model of Being
made out of string and cardboard.”
— Nanavira Thera, 1 October 1957,
on a model of Kummer’s Quartic Surface
mentioned by Eddington
A Christian view —
A formal view —
From a Log24 search for High Concept:
See also Galois Tesseract.
Comments Off on Models of Being
Monday, June 11, 2018
Arty Fact
The title was suggested by the name "ARTI" of an artificial
intelligence in the new film 2036: Origin Unknown.
The Eye of ARTI —
See also a post of May 19, "Uh-Oh" —
— and a post of June 6, "Geometry for Goyim" —
Mystery box merchandise from the 2011 J. J. Abrams film Super 8
An arty fact I prefer, suggested by the triangular computer-eye forms above —
This is from the July 29, 2012, post The Galois Tesseract.
See as well . . .
Comments Off on Arty Fact
Sunday, June 10, 2018
Pieces of April
This journal on April 16, 2018 —
Happy birthday to Pope Emeritus Benedict XVI.
Related material from another weblog in a post also dated April 16, 2018 —
"As I write this, it’s April 5, midway through the eight-day
festival of Passover. During this holiday, we Jews air our
grievances against the ancient Pharaoh who enslaved
and oppressed us, and celebrate the feats of strength
with which the Almighty delivered us from bondage —
wait a minute, I think I’m mixing up Passover with Festivus."
. . . .
"Next month: Time and Tesseracts."
From that next post, dated May 16, 2018 —
"The tesseract entered popular culture through
Madeleine L’Engle’s 'A Wrinkle in Time' . . . ."
The post's author, James Propp, notes that
" L’Engle caused some of her readers confusion
when one of the characters … the prodigy
Charles Wallace Murray [sic ] , declared 'Well, the fifth
dimension’s a tesseract.' "
Propp is not unfamiliar with prodigies:
"When I was a kid living in the Long Island suburbs,
I sometimes got called a math genius. I didn’t think
the label was apt, but I didn’t mind it; being put in
the genius box came with some pretty good perks."
— "The Genius Box," a post dated March 16, 2018
To me, Propp seems less like Charles Wallace
and more like the Prime Coordinator —
For further details, see the following synchronicity checks:
Comments Off on Pieces of April
Tuesday, May 1, 2018
Wake
Remarks on space from 1998 by sci-fi author Robert J. Sawyer quoted
here on Sunday (see the tag "Sawyer's Space") suggest a review of
rather similar remarks on space from 1977 by sci-fi author M. A. Foster
(see the tag "Foster's Space"):
Quoted here on September 26, 2012 —
"All she had to do was kick off and flow."
"I'se so silly to be flowing but I no canna stay."
Another work by Sawyer —
Comments Off on Wake
Sunday, April 29, 2018
Wednesday, April 25, 2018
Thursday, March 29, 2018
“Before Creation Itself . . .”
From the Diamond Theorem Facebook page —
A question three hours ago at that page —
"Is this Time Cube?"
Notes toward an answer —
And from Six-Set Geometry in this journal . . .
Comments Off on “Before Creation Itself . . .”
Sunday, March 11, 2018
Blackboard Jungle Continues . . .
. . . With intolerable disrespect for the word …
In particular, the word "theorem."
See also "Quantum Tesseract Theorem" in this journal.
Comments Off on Blackboard Jungle Continues . . .
Thursday, March 8, 2018
Thursday, January 25, 2018
Beware of Analogical Extension
"By an archetype I mean a systematic repertoire
of ideas by means of which a given thinker describes,
by analogical extension , some domain to which
those ideas do not immediately and literally apply."
— Max Black in Models and Metaphors
(Cornell, 1962, p. 241)
"Others … spoke of 'ultimate frames of reference' …."
— Ibid.
A "frame of reference" for the concept four quartets —
A less reputable analogical extension of the same
frame of reference —
Madeleine L'Engle in A Swiftly Tilting Planet :
"… deep in concentration, bent over the model
they were building of a tesseract:
the square squared, and squared again…."
See also the phrase Galois tesseract .
Comments Off on Beware of Analogical Extension
Wednesday, January 24, 2018
The Pentagram Papers
From a Log24 post of March 4, 2008 —
|
SINGER, ISAAC:
"Sets forth his own aims in writing for children and laments
— An Annotated Listing of Criticism
"She returned the smile, then looked across the room to
— A Swiftly Tilting Planet,
For "the dimension of time," see A Fold in Time, Time Fold,
A Swiftly Tilting Planet is a fantasy for children |
Ibid. —
The pen's point:
John Trever, Albuquerque Journal, 2/29/08
Note the figure on the cover of National Review above —
A related figure from Pentagram Design —
See, more generally, Isaac Singer in this journal.
Comments Off on The Pentagram Papers
Tuesday, January 9, 2018
Koen Thas and Quantum Theory
This post supplies some background for earlier posts tagged
Quantum Tesseract Theorem.
Comments Off on Koen Thas and Quantum Theory
Monday, January 8, 2018
Raiders of the Lost Theorem
The Quantum Tesseract Theorem —
Raiders —
A Wrinkle in Time
starring Storm Reid,
Reese Witherspoon,
Oprah Winfrey &
Mindy Kaling
Time Magazine December 25, 2017 – January 1, 2018
Comments Off on Raiders of the Lost Theorem
Thursday, December 28, 2017
Rocky Start
The above prose suggests a musical alternative to the Dec. 21
Camazotz song in the posts tagged Quantum Tesseract Theorem . . .
Comments Off on Rocky Start
Saturday, December 23, 2017
The Right Stuff
A figure related to the general connecting theorem of Koen Thas —
See also posts tagged Dirac and Geometry in this journal.
Those who prefer narrative to mathematics may, if they so fancy, call
the above Thas connecting theorem a "quantum tesseract theorem ."
Comments Off on The Right Stuff
Thursday, December 21, 2017
Wrinkles
TIME magazine, issue of December 25th, 2017 —
" In 2003, Hand worked with Disney to produce a made-for-TV movie.
Thanks to budget constraints, among other issues, the adaptation
turned out bland and uninspiring. It disappointed audiences,
L’Engle and Hand. 'This is not the dream,' Hand recalls telling herself.
'I’m sure there were people at Disney that wished I would go away.' "
Not the dream? It was, however, the nightmare, presenting very well
the encounter in Camazotz of Charles Wallace with the Tempter.
From a trailer for the latest version —
Detail:
From the 1962 book —
"There's something phoney in the whole setup, Meg thought.
There is definitely something rotten in the state of Camazotz."
Song adapted from a 1960 musical —
"In short, there's simply not
A more congenial spot
For happy-ever-aftering
Than here in Camazotz!"
Comments Off on Wrinkles
Thursday, October 19, 2017
Design Grammar***
The elementary shapes at the top of the figure below mirror
the looking-glass property of the classical Lo Shu square.
The nine shapes at top left* and their looking-glass reflection
illustrate the looking-glass reflection relating two orthogonal
Latin squares over the three digits of modulo-three arithmetic.
Combining these two orthogonal Latin squares,** we have a
representation in base three of the numbers from 0 to 8.
Adding 1 to each of these numbers yields the Lo Shu square.
* The array at top left is from the cover of
Wonder Years:
Werkplaats Typografie 1998-2008.
** A well-known construction.
*** For other instances of what might be
called "design grammar" in combinatorics,
see a slide presentation by Robin Wilson.
No reference to the work of Chomsky is
intended.
Comments Off on Design Grammar***
Saturday, September 23, 2017
The Turn of the Frame
"With respect to the story's content, the frame thus acts
both as an inclusion of the exterior and as an exclusion
of the interior: it is a perturbation of the outside at the
very core of the story's inside, and as such, it is a blurring
of the very difference between inside and outside."
— Shoshana Felman on a Henry James story, p. 123 in
"Turning the Screw of Interpretation,"
Yale French Studies No. 55/56 (1977), pp. 94-207.
Published by Yale University Press.
See also the previous post and The Galois Tesseract.
Comments Off on The Turn of the Frame
Sunday, August 27, 2017
Black Well
The “Black” of the title refers to the previous post.
For the “Well,” see Hexagram 48.
Related material —
The Galois Tesseract and, more generally, Binary Coordinate Systems.
Comments Off on Black Well
Saturday, August 26, 2017
Aesthetic Distance
Naive readers may suppose that this sort of thing is
related to what has been dubbed "geometric group theory."
It is not. See posts now tagged Aesthetic Distance.
Comments Off on Aesthetic Distance
Sunday, July 23, 2017
The Partitioned Self
Comments Off on The Partitioned Self
Tuesday, July 11, 2017
Dialogue from Plato’s Cave
Why was the Cosmic Cube named the Tesseract
in the Marvel movie series? Is there any specific reason
for the name change? According to me, Cosmic Cube
seems a nice and cooler name.
— Asked March 14, 2013, by Dhwaneet Bhatt
At least it wasn't called 'The AllSpark.'
It's not out of the realm of possibility.
— Solemnity, March 14, 2013
Comments Off on Dialogue from Plato’s Cave
Saturday, June 3, 2017
Expanding the Spielraum (Continued*)
Or: The Square
"What we do may be small, but it has
a certain character of permanence."
— G. H. Hardy
* See Expanding the Spielraum in this journal.
Comments Off on Expanding the Spielraum (Continued*)
Tuesday, May 23, 2017
Saturday, May 20, 2017
The Ludicrous Extreme
From a review of the 2016 film "Arrival" —
"A seemingly off-hand reference to Abbott and Costello
is our gateway. In a movie as generally humorless as Arrival,
the jokes mean something. Ironically, it is Donnelly, not Banks,
who initiates the joke, naming the verbally inexpressive
Heptapod aliens after the loquacious Classical Hollywood
comedians. The squid-like aliens communicate via those beautiful,
cryptic images. Those signs, when thoroughly comprehended,
open the perceiver to a nonlinear conception of time; this is
Sapir-Whorf taken to the ludicrous extreme."
— Jordan Brower in the Los Angeles Review of Books
Further on in the review —
"Banks doesn’t fully understand the alien language, but she
knows it well enough to get by. This realization emerges
most evidently when Banks enters the alien ship and, floating
alongside Costello, converses with it in their picture-language.
She asks where Abbott is, and it responds — as presented
in subtitling — that Abbott 'is death process.'
'Death process' — dying — is not idiomatic English, and what
we see, written for us, is not a perfect translation but a
rendering of Banks’s understanding. This, it seems to me, is a
crucial moment marking the hard limit of a human mind,
working within the confines of human language to understand
an ultimately intractable xenolinguistic system."
For what may seem like an intractable xenolinguistic system to
those whose experience of mathematics is limited to portrayals
by Hollywood, see the previous post —
van Lint and Wilson Meet the Galois Tesseract.
The death process of van Lint occurred on Sept. 28, 2004.
Comments Off on The Ludicrous Extreme
Tuesday, May 2, 2017
Image Albums
Pinterest boards uploaded to the new m759.net/piwigo —
Update of May 2 —
Update of May 3 —
Update of May 8 —
Art Space board created at Pinterest
Comments Off on Image Albums
Saturday, March 25, 2017
Twin Pillars of Symmetry
The phrase "twin pillars" in a New York Times Fashion & Style
article today suggests a look at another pair of pillars —
This pair, from the realm of memory, history, and geometry disparaged
by the late painter Mark Rothko, might be viewed by Rothko
as "parodies of ideas (which are ghosts)." (See the previous post.)
For a relationship between a 3-dimensional simplex and the {4, 3, 3},
see my note from May 21, 2014, on the tetrahedron and the tesseract.
Comments Off on Twin Pillars of Symmetry
Sunday, March 19, 2017
Norwegian Sermon
Comments Off on Norwegian Sermon
Saturday, December 10, 2016
Folk Etymology
Images from Burkard Polster's Geometrical Picture Book —
See as well in this journal the large Desargues configuration, with
15 points and 20 lines instead of 10 points and 10 lines as above.
Exercise: Can the large Desargues configuration be formed
by adding 5 points and 10 lines to the above Polster model
of the small configuration in such a way as to preserve
the small-configuration model's striking symmetry?
(Note: The related figure below from May 21, 2014, is not
necessarily very helpful. Try the Wolfram Demonstrations
model, which requires a free player download.)
Labeling the Tetrahedral Model (Click to enlarge) —
Related folk etymology (see point a above) —
Related literature —
The concept of "fire in the center" at The New Yorker ,
issue dated December 12, 2016, on pages 38-39 in the
poem by Marsha de la O titled "A Natural History of Light."
Cézanne's Greetings.
Comments Off on Folk Etymology
Friday, December 9, 2016
Snow Dance
See Ballet Blanc in this journal.
For a darker perspective, click on the image below.
See also Cartier in The Hexagon of Opposition.
Happy birthday to Kirk Douglas.
Comments Off on Snow Dance
Wednesday, October 5, 2016
Sources
From a Google image search yesterday —
Sources (left to right, top to bottom) —
Math Guy (July 16, 2014)
The Galois Tesseract (Sept. 1, 2011)
The Full Force of Roman Law (April 21, 2014)
A Great Moonshine (Sept. 25, 2015)
A Point of Identity (August 8, 2016)
Pascal via Curtis (April 6, 2013)
Correspondences (August 6, 2011)
Symmetric Generation (Sept. 21, 2011)
Comments Off on Sources
Tuesday, August 16, 2016
Midnight Narrative
The images in the previous post do not lend themselves
to any straightforward narrative. Two portions of the
large image search are, however, suggestive —
.jpg){kind=link}
Cross and Boolean lattice.
The improvised cross in the second pair of images
is perhaps being wielded to counteract the
Boole of the first pair of images. See the heading
of the webpage that is the source of the lattice
diagram toward which the cross is directed —
Update of 10 am on August 16, 2016 —
See also Atiyah on the theology of
(Boolean) algebra vs. (Galois) geometry:
Comments Off on Midnight Narrative
Friday, July 15, 2016
Autistic Enchantment*
Robert Nye, author of the novel Falstaff , reportedly died
at 77 on July 2, 2016.
Harvey D. Heinz, expert on magic squares, cubes,
tesseracts, etc., reportedly died at 82 on July 6, 2013.
In memoriam —
From the date of Nye's death:
From Nye's book:
From the date of Heinz's death:
* See also a search for the title in this journal.
Comments Off on Autistic Enchantment*
Wednesday, May 25, 2016
Framework
"Studies of spin-½ theories in the framework of projective geometry
have been undertaken before." — Y. Jack Ng and H. van Dam,
February 20, 2009
For one such framework,* see posts from that same date
four years earlier — February 20, 2005.
* A 4×4 array. See the 1977, 1978, and 1986 versions by
Steven H. Cullinane, the 1987 version by R. T. Curtis, and
the 1988 Conway-Sloane version illustrated below —
Cullinane, 1977
Cullinane, 1978
Cullinane, 1986
Curtis, 1987
Update of 10:42 PM ET on Sunday, June 19, 2016 —
The above images are precursors to …
Conway and Sloane, 1988
Update of 10 AM ET Sept. 16, 2016 — The excerpt from the
1977 "Diamond Theory" article was added above.
Comments Off on Framework
Wednesday, May 11, 2016
Jewel of Odin
The tesseract in last night's post Game Theory
suggests a search in Log24 for "Jewel of Odin."
See also Trinkets.
Comments Off on Jewel of Odin
Tuesday, May 10, 2016
Game Theory
The following passage appeared in this journal
on the night of May 23-24, 2015.
The afternoon of May 23, 2015, was significant
for devotees of mathematics and narrative.
Comments Off on Game Theory