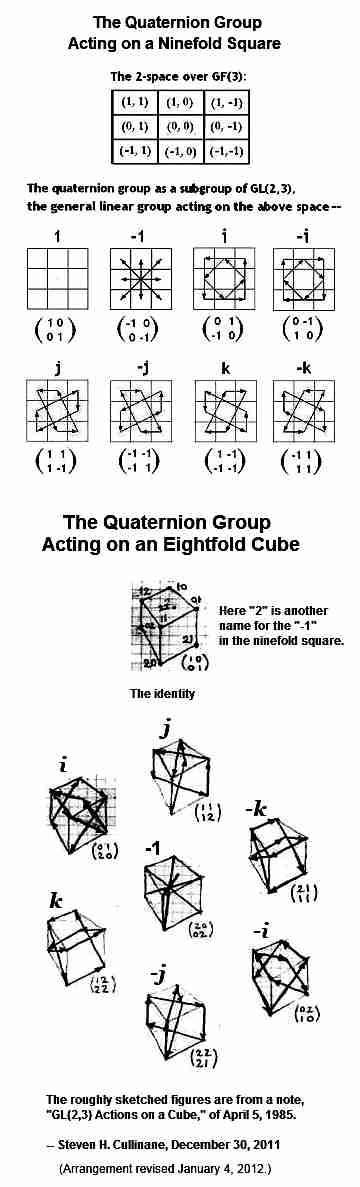
|
Definition of Epiphany
From James Joyce’s Stephen Hero , first published posthumously in 1944. The excerpt below is from a version edited by John J. Slocum and Herbert Cahoon (New York: New Directions Press, 1959).
Three Times:
… By an epiphany he meant a sudden spiritual manifestation, whether in the vulgarity of speech or of gesture or in a memorable phase of the mind itself. He believed that it was for the man of letters to record these epiphanies with extreme care, seeing that they themselves are the most delicate and evanescent of moments. He told Cranly that the clock of the Ballast Office was capable of an epiphany. Cranly questioned the inscrutable dial of the Ballast Office with his no less inscrutable countenance:
— Yes, said Stephen. I will pass it time after time, allude to it, refer to it, catch a glimpse of it. It is only an item in the catalogue of Dublin’s street furniture. Then all at once I see it and I know at once what it is: epiphany.
— What?
— Imagine my glimpses at that clock as the gropings of a spiritual eye which seeks to adjust its vision to an exact focus. The moment the focus is reached the object is epiphanised. It is just in this epiphany that I find the third, the supreme quality of beauty.
— Yes? said Cranly absently.
— No esthetic theory, pursued Stephen relentlessly, is of any value which investigates with the aid of the lantern of tradition. What we symbolise in black the Chinaman may symbolise in yellow: each has his own tradition. Greek beauty laughs at Coptic beauty and the American Indian derides them both. It is almost impossible to reconcile all tradition whereas it is by no means impossible to find the justification of every form of beauty which has ever been adored on the earth by an examination into the mechanism of esthetic apprehension whether it be dressed in red, white, yellow or black. We have no reason for thinking that the Chinaman has a different system of digestion from that which we have though our diets are quite dissimilar. The apprehensive faculty must be scrutinised in action.
— Yes …
— You know what Aquinas says: The three things requisite for beauty are, integrity, a wholeness, symmetry and radiance. Some day I will expand that sentence into a treatise. Consider the performance of your own mind when confronted with any object, hypothetically beautiful. Your mind to apprehend that object divides the entire universe into two parts, the object, and the void which is not the object. To apprehend it you must lift it away from everything else: and then you perceive that it is one integral thing, that is a thing. You recognise its integrity. Isn’t that so?
— And then?
— That is the first quality of beauty: it is declared in a simple sudden synthesis of the faculty which apprehends. What then? Analysis then. The mind considers the object in whole and in part, in relation to itself and to other objects, examines the balance of its parts, contemplates the form of the object, traverses every cranny of the structure. So the mind receives the impression of the symmetry of the object. The mind recognises that the object is in the strict sense of the word, a thing , a definitely constituted entity. You see?
— Let us turn back, said Cranly.
They had reached the corner of Grafton St and as the footpath was overcrowded they turned back northwards. Cranly had an inclination to watch the antics of a drunkard who had been ejected from a bar in Suffolk St but Stephen took his arm summarily and led him away.
— Now for the third quality. For a long time I couldn’t make out what Aquinas meant. He uses a figurative word (a very unusual thing for him) but I have solved it. Claritas is quidditas . After the analysis which discovers the second quality the mind makes the only logically possible synthesis and discovers the third quality. This is the moment which I call epiphany. First we recognise that the object is one integral thing, then we recognise that it is an organised composite structure, a thing in fact: finally, when the relation of the parts is exquisite, when the parts are adjusted to the special point, we recognise that it is that thing which it is. Its soul, its whatness, leaps to us from the vestment of its appearance. The soul of the commonest object, the structure of which is so adjusted, seems to us radiant. The object achieves its epiphany.
Having finished his argument Stephen walked on in silence. He felt Cranly’s hostility and he accused himself of having cheapened the eternal images of beauty. For the first time, too, he felt slightly awkward in his friend’s company and to restore a mood of flippant familiarity he glanced up at the clock of the Ballast Office and smiled:
— It has not epiphanised yet, he said.
|