Ideas and Art, Part III
The first idea was not our own. Adam
In Eden was the father of Descartes…
— Wallace Stevens, from
Notes Toward a Supreme Fiction
"Quaedam ex his tanquam rerum imagines sunt, quibus solis proprie convenit ideae nomen: ut cùm hominem, vel Chimaeram, vel Coelum, vel Angelum, vel Deum cogito."
— Descartes, Meditationes III, 5
"Of my thoughts some are, as it were, images of things, and to these alone properly belongs the name idea; as when I think [represent to my mind] a man, a chimera, the sky, an angel or God."
— Descartes, Meditations III, 5
Begin, ephebe, by perceiving the idea
Of this invention, this invented world,
The inconceivable idea of the sun.
You must become an ignorant man again
And see the sun again with an ignorant eye
And see it clearly in the idea of it.
— Wallace Stevens, from
Notes Toward a Supreme Fiction
"… Quinimo in multis saepe magnum discrimen videor deprehendisse: ut, exempli causâ, duas diversas solis ideas apud me invenio, unam tanquam a sensibus haustam, & quae maxime inter illas quas adventitias existimo est recensenda, per quam mihi valde parvus apparet, aliam verò ex rationibus Astronomiae desumptam, hoc est ex notionibus quibusdam mihi innatis elicitam, vel quocumque alio modo a me factam, per quam aliquoties major quàm terra exhibetur; utraque profecto similis eidem soli extra me existenti esse non potest, & ratio persuadet illam ei maxime esse dissimilem, quae quàm proxime ab ipso videtur emanasse."
— Descartes, Meditationes III, 11
"… I have observed, in a number of instances, that there was a great difference between the object and its idea. Thus, for example, I find in my mind two wholly diverse ideas of the sun; the one, by which it appears to me extremely small draws its origin from the senses, and should be placed in the class of adventitious ideas; the other, by which it seems to be many times larger than the whole earth, is taken up on astronomical grounds, that is, elicited from certain notions born with me, or is framed by myself in some other manner. These two ideas cannot certainly both resemble the same sun; and reason teaches me that the one which seems to have immediately emanated from it is the most unlike."
— Descartes, Meditations III, 11
"Et quamvis forte una idea ex aliâ nasci possit, non tamen hîc datur progressus in infinitum, sed tandem ad aliquam primam debet deveniri, cujus causa sit in star archetypi, in quo omnis realitas formaliter contineatur, quae est in ideâ tantùm objective."
— Descartes, Meditationes III, 15
"And although an idea may give rise to another idea, this regress cannot, nevertheless, be infinite; we must in the end reach a first idea, the cause of which is, as it were, the archetype in which all the reality [or perfection] that is found objectively [or by representation] in these ideas is contained formally [and in act]."
— Descartes, Meditations III, 15
Michael Bryson in an essay on Stevens's "Notes Toward a Supreme Fiction,"
The Quest for the Fiction of the Absolute:
"Canto nine considers the movement of the poem between the particular and the general, the immanent and the transcendent: "The poem goes from the poet's gibberish to / The gibberish of the vulgate and back again. / Does it move to and fro or is it of both / At once?" The poet, the creator-figure, the shadowy god-figure, is elided, evading us, "as in a senseless element." The poet seeks to find the transcendent in the immanent, the general in the particular, trying "by a peculiar speech to speak / The peculiar potency of the general." In playing on the senses of "peculiar" as particular and strange or uncanny, these lines play on the mystical relation of one and many, of concrete and abstract."
Brian Cronin in Foundations of Philosophy:
"The insight is constituted precisely by 'seeing' the idea in the image, the intelligible in the sensible, the universal in the particular, the abstract in the concrete. We pivot back and forth between images and ideas as we search for the correct insight."
— From Ch. 2, Identifying Direct Insights
Michael Bryson in an essay on Stevens's "Notes Toward a Supreme Fiction":
"The fourth canto returns to the theme of opposites. 'Two things of opposite natures seem to depend / On one another . . . . / This is the origin of change.' Change resulting from a meeting of opposities is at the root of Taoism: 'Tao produced the One. / The One produced the two. / The two produced the three. / And the three produced the ten thousand things' (Tao Te Ching 42) …."
|
From an entry of March 7, 2004:
From the web page
Introduction to the I Ching–
By Richard Wilhelm:
"He who has perceived the meaning of change fixes his attention no longer on transitory individual things but on the immutable, eternal law at work in all change. This law is the tao of Lao-tse, the course of things, the principle of the one in the many. That it may become manifest, a decision, a postulate, is necessary. This fundamental postulate is the 'great primal beginning' of all that exists, t'ai chi — in its original meaning, the 'ridgepole.' Later Chinese philosophers devoted much thought to this idea of a primal beginning. A still earlier beginning, wu chi, was represented by the symbol of a circle. Under this conception, t'ai chi was represented by the circle divided into the light and the dark, yang and yin,
 . .
This symbol has also played a significant part in India and Europe. However, speculations of a gnostic-dualistic character are foreign to the original thought of the I Ching; what it posits is simply the ridgepole, the line. With this line, which in itself represents oneness, duality comes into the world, for the line at the same time posits an above and a below, a right and left, front and back-in a word, the world of the opposites."
The t'ai chi symbol is also illustrated on the web page Cognitive Iconology, which says that
"W.J.T. Mitchell calls 'iconology'
a study of the 'logos'
(the words, ideas, discourse, or 'science')
of 'icons' (images, pictures, or likenesses).
It is thus a 'rhetoric of images'
(Iconology: Image, Text, Ideology, p. 1)."
A variation on the t'ai chi symbol appears in a log24.net entry for March 5:

The Line,
by S. H. Cullinane
See too my web page Logos and Logic, which has the following:
"The beautiful in mathematics resides in contradiction. Incommensurability, logoi alogoi, was the first splendor in mathematics."
— Simone Weil, Oeuvres Choisies, ed. Quarto, Gallimard, 1999, p. 100

Logos Alogos,
by S. H. Cullinane
In the conclusion of Section 3, Canto X, of "Notes," Stevens says
"They will get it straight one day
at the Sorbonne.
We shall return at twilight
from the lecture
Pleased that
the irrational is rational…."
This is the logoi alogoi of Simone Weil.
|
In "Notes toward a Supreme Fiction,"
Wallace Stevens lists three criteria
for a work of the imagination:
It Must Be Abstract

The Line,
by S.H. Cullinane
It Must Change

The 24,
by S. H. Cullinane
It Must Give Pleasure

Puzzle,
by S. H. Cullinane
Related material:
Logos and Logic.














.jpg)



















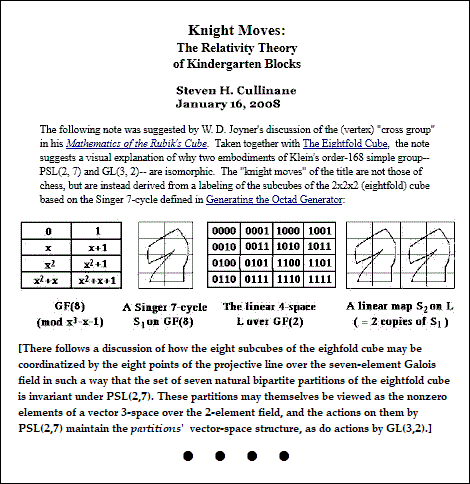



































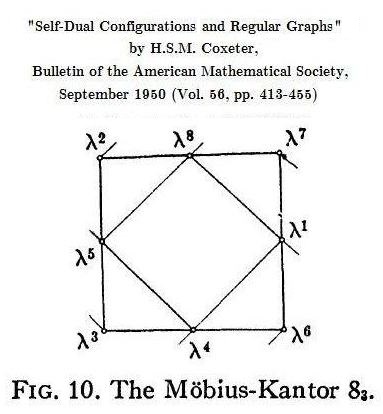













































































 .
.



















