See also Cube Symmetry Planes in this journal.
Monday, May 19, 2014
Tuesday, March 2, 2010
Symmetry and Automorphisms
From the conclusion of Weyl's Symmetry —
One example of Weyl's "structure-endowed entity" is a partition of a six-element set into three disjoint two-element sets– for instance, the partition of the six faces of a cube into three pairs of opposite faces.
The automorphism group of this faces-partition contains an order-8 subgroup that is isomorphic to the abstract group C2×C2×C2 of order eight–
The action of Klein's simple group of order 168 on the Cayley diagram of C2×C2×C2 in yesterday's post furnishes an example of Weyl's statement that
"… one may ask with respect to a given abstract group: What is the group of its automorphisms…?"
Comments Off on Symmetry and Automorphisms
Thursday, April 11, 2013
Naked Art
The New Yorker on Cubism:
"The style wasn’t new, exactly— or even really a style,
in its purest instances— though it would spawn no end
of novelties in art and design. Rather, it stripped naked
certain characteristics of all pictures. Looking at a Cubist
work, you are forced to see how you see. This may be
gruelling, a gymnasium workout for eye and mind.
It pays off in sophistication."
— Online "Culture Desk" weblog, posted today by Peter Schjeldahl
Non-style from 1911:
See also Cube Symmetry Planes in this journal.
A comment at The New Yorker related to Schjeldahl's phrase "stripped naked"—
"Conceptualism is the least seductive modern-art movement."
POSTED 4/11/2013, 3:54:37 PM BY CHRISKELLEY
(The "conceptualism" link was added to the quoted comment.)
Comments Off on Naked Art
Saturday, March 26, 2022
Box Geometry: Space, Group, Art (Work in Progress)
| Name Tag | .Space | .Group | .Art |
|---|---|---|---|
| Box4 |
2×2 square representing the four-point finite affine geometry AG(2,2). (Box4.space) |
S4 = AGL(2,2) (Box4.group) |
(Box4.art) |
| Box6 |
3×2 (3-row, 2-column) rectangular array representing the elements of an arbitrary 6-set. |
S6 | |
| Box8 | 2x2x2 cube or 4×2 (4-row, 2-column) array. | S8 or A8 or AGL(3,2) of order 1344, or GL(3,2) of order 168 | |
| Box9 | The 3×3 square. | AGL(2,3) or GL(2,3) | |
| Box12 | The 12 edges of a cube, or a 4×3 array for picturing the actions of the Mathieu group M12. | Symmetries of the cube or elements of the group M12 | |
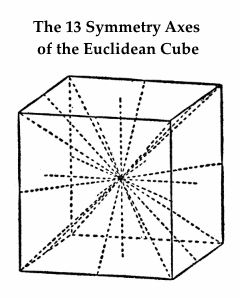
| Box13 | The 13 symmetry axes of the cube. | Symmetries of the cube. | |
| Box15 |
The 15 points of PG(3,2), the projective geometry of 3 dimensions over the 2-element Galois field. |
Collineations of PG(3,2) | |
| Box16 |
The 16 points of AG(4,2), the affine geometry of 4 dimensions over the 2-element Galois field. |
AGL(4,2), the affine group of |
|
| Box20 | The configuration representing Desargues's theorem. | ||
| Box21 | The 21 points and 21 lines of PG(2,4). | ||
| Box24 | The 24 points of the Steiner system S(5, 8, 24). | ||
| Box25 | A 5×5 array representing PG(2,5). | ||
| Box27 |
The 3-dimensional Galois affine space over the 3-element Galois field GF(3). |
||
| Box28 | The 28 bitangents of a plane quartic curve. | ||
| Box32 |
Pair of 4×4 arrays representing orthogonal Latin squares. |
Used to represent elements of AGL(4,2) |
|
| Box35 |
A 5-row-by-7-column array representing the 35 lines in the finite projective space PG(3,2) |
PGL(3,2), order 20,160 | |
| Box36 | Eurler's 36-officer problem. | ||
| Box45 | The 45 Pascal points of the Pascal configuration. | ||
| Box48 | The 48 elements of the group AGL(2,3). | AGL(2,3). | |
| Box56 |
The 56 three-sets within an 8-set or |
||
| Box60 | The Klein configuration. | ||
| Box64 | Solomon's cube. |
— Steven H. Cullinane, March 26-27, 2022
Comments Off on Box Geometry: Space, Group, Art (Work in Progress)
Saturday, May 23, 2020
Structure for Linguists
"MIT professor of linguistics Wayne O’Neil died on March 22
at his home in Somerville, Massachusetts."
— MIT Linguistics, May 1, 2020
The "deep structure" above is the plane cutting the cube in a hexagon
(as in my note Diamonds and Whirls of September 1984).
See also . . .
Comments Off on Structure for Linguists
Sunday, January 13, 2019
Sunday the Thirteenth (Revisited)
Comments Off on Sunday the Thirteenth (Revisited)
Tuesday, December 26, 2017
Raiders of the Lost Stone
Two Students of Structure
A comment on Sean Kelly's Christmas Morning column on "aliveness"
in the New York Times philosophy series The Stone —
Diana Senechal's 1999 doctoral thesis at Yale was titled
"Diabolical Structures in the Poetics of Nikolai Gogol."
Her mother, Marjorie Senechal, has written extensively on symmetry
and served as editor-in-chief of The Mathematical Intelligencer .
From a 2013 memoir by Marjorie Senechal —
|
"While I was in Holland my enterprising student assistant at Smith had found, in Soviet Physics – Crystallography, an article by N. N. Sheftal' on tetrahedral penetration twins. She gave it to me on my return. It was just what I was looking for. The twins Sheftal' described had evidently begun as (111) contact twins, with the two crystallites rotated 60o with respect to one another. As they grew, he suggested, each crystal overgrew the edges of the other and proceeded to spread across the adjacent facet. When all was said and done, they looked like they'd grown through each other, but the reality was over-and-around. Brilliant! I thought. Could I apply this to cubes? No, evidently not. Cube facets are all (100) planes. But . . . these crystals might not have been cubes in their earliest stages, when twinning occurred! I wrote a paper on "The mechanism of certain growth twins of the penetration type" and sent it to Martin Buerger, editor of Neues Jarbuch für Mineralogie. This was before the Wrinch symposium; I had never met him. Buerger rejected it by return mail, mostly on the grounds that I hadn't quoted any of Buerger's many papers on twinning. And so I learned about turf wars in twin domains. In fact I hadn't read his papers but I quickly did. I added a reference to one of them, the paper was published, and we became friends.[5]
After reading Professor Sheftal's paper I wrote to him in Moscow; a warm and encouraging correspondence ensued, and we wrote a paper together long distance.[6] Then I heard about the scientific exchanges between the Academies of Science of the USSR and USA. I applied to spend a year at the Shubnikov Institute for Crystallography, where Sheftal' worked. I would, I proposed, study crystal growth with him, and color symmetry with Koptsik. To my delight, I was accepted for an 11-month stay. Of course the children, now 11 and 14, would come too and attend Russian schools and learn Russian; they'd managed in Holland, hadn't they? Diana, my older daughter, was as delighted as I was. We had gone to Holland on a Russian boat, and she had fallen in love with the language. (Today she holds a Ph.D. in Slavic Languages and Literature from Yale.) . . . . |
Philosophy professors and those whose only interest in mathematics
is as a path to the occult may consult the Log24 posts tagged Tsimtsum.
Comments Off on Raiders of the Lost Stone
Tuesday, June 20, 2017
All-Spark Notes
"For years, the AllSpark rested, sitting dormant
like a giant, useless art installation."
— Vinnie Mancuso at Collider.com yesterday
Related material —
Giant, useless art installation —
Sol LeWitt at MASS MoCA. See also LeWitt in this journal.
Comments Off on All-Spark Notes
Wednesday, May 4, 2016
Solomon Golomb, 1932-2016
Material related to the previous post, "Symmetry" —
This is the group of "8 rigid motions
generated by reflections in midplanes"
of "Solomon's Cube."
Material from this journal on May 1, the date of Golomb's death —
"Weitere Informationen zu diesem Themenkreis
finden sich unter http://www.encyclopediaofmath.org/
index.php/Cullinane_diamond_theorem und
http://finitegeometry.org/sc/gen/coord.html ."
Comments Off on Solomon Golomb, 1932-2016
Tuesday, February 9, 2016
Cubism
The hexagons above appear also in Gary W. Gibbons,
"The Kummer Configuration and the Geometry of Majorana Spinors,"
1993, in a cube model of the Kummer 166 configuration —
Related material — The Religion of Cubism (May 9, 2003).
Comments Off on Cubism
Thursday, December 17, 2015
Hint of Reality
From an article* in Proceedings of Bridges 2014 —
|
As artists, we are particularly interested in the symmetries of real world physical objects. Three natural questions arise: 1. Which groups can be represented as the group of symmetries of some real-world physical object? 2. Which groups have actually been represented as the group of symmetries of some real-world physical object? 3. Are there any glaring gaps – small, beautiful groups that should have a physical representation in a symmetric object but up until now have not? |
The article was cited by Evelyn Lamb in her Scientific American
weblog on May 19, 2014.
The above three questions from the article are relevant to a more
recent (Oct. 24, 2015) remark by Lamb:
"… finite projective planes [in particular, the 7-point Fano plane,
about which Lamb is writing] seem like a triumph of purely
axiomatic thinking over any hint of reality…."
For related hints of reality, see Eightfold Cube in this journal.
* "The Quaternion Group as a Symmetry Group," by Vi Hart and Henry Segerman
Comments Off on Hint of Reality
Sunday, November 30, 2014
Two Physical Models of the Fano Plane
The seven symmetry axes of the regular tetrahedron
are of two types: vertex-to-face and edge-to-edge.
Take these axes as the "points" of a Fano plane.
Each of the tetrahedron's six reflection planes contains
two vertex-to-face axes and one edge-to-edge axis.
Take these six planes as six of the "lines" of a Fano
plane. Then the seventh line is the set of three
edge-to-edge axes.
(The Fano tetrahedron is not original with me.
See Polster's 1998 A Geometrical Picture Book , pp. 16-17.)
There are three reflection planes parallel to faces
of the cube. Take the seven nonempty subsets of
the set of these three planes as the "points" of a
Fano plane. Define the Fano "lines" as those triples
of these seven subsets in which each member of
the triple is the symmetric-difference sum of the
other two members.
(This is the eightfold cube discussed at finitegeometry.org.)
Comments Off on Two Physical Models of the Fano Plane
Wednesday, November 26, 2014
Class Act
Update of Nov. 30, 2014 —
For further information on the geometry in
the remarks by Eberhart below, see
pp. 16-17 of A Geometrical Picture Book ,
by Burkard Polster (Springer, 1998). Polster
cites a different article by Lemay.
A search for background to the exercise in the previous post
yields a passage from the late Stephen Eberhart:
|
The first three primes p = 2, 3, and 5 therefore yield finite projective planes with 7, 13, and 31 points and lines, respectively. But these are just the numbers of symmetry axes of the five regular solids, as described in Plato's Timaeus : The tetrahedron has 4 pairs of face planes and corner points + 3 pairs of opposite edges, totalling 7 axes; the cube has 3 pairs of faces + 6 pairs of edges + 4 pairs of corners, totalling 13 axes (the octahedron simply interchanges the roles of faces and corners); and the pentagon dodecahedron has 6 pairs of faces + 15 pairs of edges + 10 pairs of corners, totalling 31 axes (the icosahedron again interchanging roles of faces and corners). This is such a suggestive result, one would expect to find it dealt with in most texts on related subjects; instead, while "well known to those who well know such things" (as Richard Guy likes to quip), it is scarcely to be found in the formal literature [9]. The reason for the common numbers, it turns out, is that the groups of symmetry motions of the regular solids are subgroups of the groups of collineations of the respective finite planes, a face axis being different from an edge axis of a regular solid but all points of a projective plane being alike, so the latter has more symmetries than the former. [9] I am aware only of a series of in-house publications by Fernand Lemay of the Laboratoire de Didactique, Faculté des Sciences de I 'Éducation, Univ. Laval, Québec, in particular those collectively titled Genèse de la géométrie I-X.
— Stephen Eberhart, Dept. of Mathematics, |
Eberhart died of bone cancer in 2003. A memorial by his
high school class includes an Aug. 7, 2003, transcribed
letter from Eberhart to a classmate that ends…
|
… I earned MA’s in math (UW, Seattle) and history (UM, Missoula) where a math/history PhD program had been announced but canceled. So 1984 to 2002 I taught math (esp. non-Euclidean geometry) at C.S.U. Northridge. It’s been a rich life. I’m grateful. Steve |
See also another informative BRIDGES paper by Eberhart
on mathematics and the seven traditional liberal arts.
Comments Off on Class Act
Tuesday, November 25, 2014
Euclidean-Galois Interplay
For previous remarks on this topic, as it relates to
symmetry axes of the cube, see previous posts tagged Interplay.
The above posts discuss, among other things, the Galois
projective plane of order 3, with 13 points and 13 lines.
These Galois points and lines may be modeled in Euclidean geometry
by the 13 symmetry axes and the 13 rotation planes
of the Euclidean cube. They may also be modeled in Galois geometry
by subsets of the 3x3x3 Galois cube (vector 3-space over GF(3)).
The 3×3×3 Galois Cube
Exercise: Is there any such analogy between the 31 points of the
order-5 Galois projective plane and the 31 symmetry axes of the
Euclidean dodecahedron and icosahedron? Also, how may the
31 projective points be naturally pictured as lines within the
5x5x5 Galois cube (vector 3-space over GF(5))?
Update of Nov. 30, 2014 —
For background to the above exercise, see
pp. 16-17 of A Geometrical Picture Book ,
by Burkard Polster (Springer, 1998), esp.
the citation to a 1983 article by Lemay.
Comments Off on Euclidean-Galois Interplay
Wednesday, January 22, 2014
A Riddle for Davos
Einstein and Thomas Mann, Princeton, 1938
See also the life of Diogenes Allen, a professor at Princeton
Theological Seminary, a life that reportedly ended on the date—
January 13, 2013— of the above Log24 post.
January 13 was also the dies natalis of St. James Joyce.
Some related reflections —
"Praeterit figura huius mundi " — I Corinthians 7:31 —
|
Conclusion of of "The Dead," by James Joyce— The air of the room chilled his shoulders. He stretched himself cautiously along under the sheets and lay down beside his wife. One by one, they were all becoming shades. Better pass boldly into that other world, in the full glory of some passion, than fade and wither dismally with age. He thought of how she who lay beside him had locked in her heart for so many years that image of her lover's eyes when he had told her that he did not wish to live. Generous tears filled Gabriel's eyes. He had never felt like that himself towards any woman, but he knew that such a feeling must be love. The tears gathered more thickly in his eyes and in the partial darkness he imagined he saw the form of a young man standing under a dripping tree. Other forms were near. His soul had approached that region where dwell the vast hosts of the dead. He was conscious of, but could not apprehend, their wayward and flickering existence. His own identity was fading out into a grey impalpable world: the solid world itself, which these dead had one time reared and lived in, was dissolving and dwindling. A few light taps upon the pane made him turn to the window. It had begun to snow again. He watched sleepily the flakes, silver and dark, falling obliquely against the lamplight. The time had come for him to set out on his journey westward. Yes, the newspapers were right: snow was general all over Ireland. It was falling on every part of the dark central plain, on the treeless hills, falling softly upon the Bog of Allen and, farther westward, softly falling into the dark mutinous Shannon waves. It was falling, too, upon every part of the lonely churchyard on the hill where Michael Furey lay buried. It lay thickly drifted on the crooked crosses and headstones, on the spears of the little gate, on the barren thorns. His soul swooned slowly as he heard the snow falling faintly through the universe and faintly falling, like the descent of their last end, upon all the living and the dead. |
Comments Off on A Riddle for Davos
Tuesday, July 9, 2013
Vril Chick
Profile picture of "Jo Lyxe" (Josefine Lyche) at Vimeo—
Compare to an image of Vril muse Maria Orsitsch.
From the catalog of a current art exhibition
(25 May – 31 August, 2013) in Norway,
I DE LANGE NÆTTER —
|
Josefine Lyche
Keywords (to help place my artwork in the (See also the original catalog page.) |
Clearly most of this (the non-highlighted parts) was taken
from my webpage Diamond Theory. I suppose I should be
flattered, but I am not thrilled to be associated with the
(apparently fictional) Vril Society.
For some background, see (for instance)
Conspiracy Theories and Secret Societies for Dummies .
Comments Off on Vril Chick
Saturday, May 11, 2013
Core
Promotional description of a new book:
"Like Gödel, Escher, Bach before it, Surfaces and Essences will profoundly enrich our understanding of our own minds. By plunging the reader into an extraordinary variety of colorful situations involving language, thought, and memory, by revealing bit by bit the constantly churning cognitive mechanisms normally completely hidden from view, and by discovering in them one central, invariant core— the incessant, unconscious quest for strong analogical links to past experiences— this book puts forth a radical and deeply surprising new vision of the act of thinking."
"Like Gödel, Escher, Bach before it…."
Or like Metamagical Themas .
Rubik core:
Non- Rubik cores:
|
Of the odd nxnxn cube:
|
Of the even nxnxn cube:
|
Related material: The Eightfold Cube and…
"A core component in the construction
is a 3-dimensional vector space V over F2 ."
— Page 29 of "A twist in the M24 moonshine story,"
by Anne Taormina and Katrin Wendland.
(Submitted to the arXiv on 13 Mar 2013.)
Comments Off on Core
Tuesday, February 19, 2013
Configurations
Yesterday's post Permanence dealt with the cube
as a symmetric model of the finite projective plane
PG(2,3), which has 13 points and 13 lines. The points
and lines of the finite geometry occur in the cube as
the 13 axes of symmetry and the 13 planes through
the center perpendicular to those axes. If the three
axes lying in a plane that cuts the cube in a hexagon
are supplemented by the axis perpendicular to that
plane, each plane is associated with four axes and,
dually, each axis is associated with four planes.
My web page on this topic, Cubist Geometries, was
written on February 27, 2010, and first saved to the
Internet Archive on Oct. 4, 2010.
For a more recent treatment of this topic that makes
exactly the same points as the 2010 page, see p. 218
of Configurations from a Graphical Viewpoint , by
Tomaž Pisanski and Brigitte Servatius, published by
Springer on Sept. 23, 2012 (date from both Google
Books and Amazon.com):
For a similar 1998 treatment of the topic, see Burkard Polster's
A Geometrical Picture Book (Springer, 1998), pp. 103-104.
The Pisanski-Servatius book reinforces my argument of Jan. 13, 2013,
that the 13 planes through the cube's center that are perpendicular
to the 13 axes of symmetry of the cube should be called the cube's
symmetry planes , contradicting the usual use of of that term.
That argument concerns the interplay between Euclidean and
Galois geometry. Pisanski and Servatius (and, in 1998, Polster)
emphasize the Euclidean square and cube as guides* to
describing the structure of a Galois space. My Jan. 13 argument
uses Galois structures as a guide to re-describing those of Euclid .
(For a similar strategy at a much more sophisticated level,
see a recent Harvard Math Table.)
Related material: Remarks on configurations in this journal
during the month that saw publication of the Pisanski-Servatius book.
* Earlier guides: the diamond theorem (1978), similar theorems for
2x2x2 (1984) and 4x4x4 cubes (1983), and Visualizing GL(2,p)
(1985). See also Spaces as Hypercubes (2012).
Comments Off on Configurations
Monday, February 18, 2013
Permanence
Inscribed hexagon (1984)
The well-known fact that a regular hexagon
may be inscribed in a cube was the basis
in 1984 for two ways of coloring the faces
of a cube that serve to illustrate some graphic
aspects of embodied Galois geometry—
Inscribed hexagon (2013)
A redefinition of the term "symmetry plane"
also uses the well-known inscription
of a regular hexagon in the cube—
Related material
"Here is another way to present the deep question 1984 raises…."
— "The Quest for Permanent Novelty," by Michael W. Clune,
The Chronicle of Higher Education , Feb. 11, 2013
“What we do may be small, but it has a certain character of permanence.”
— G. H. Hardy, A Mathematician’s Apology
Comments Off on Permanence
Sunday, January 13, 2013
Spinning in Infinity
A note for day 13 of 2013
How the cube's 13 symmetry planes*
are related to the finite projective plane
of order 3, with 13 points and 13 lines—
For some background, see Cubist Geometries.
* This is not the standard terminology. Most sources count
only the 9 planes fixed pointwise under reflections as
"symmetry planes." This of course obscures the connection
with finite geometry.
Comments Off on Spinning in Infinity
Saturday, January 14, 2012
Defining Form (continued)
Detail of Sylvie Donmoyer picture discussed
here on January 10—
The "13" tile may refer to the 13 symmetry axes
in the 3x3x3 Galois cube, or the corresponding
13 planes through the center in that cube. (See
this morning's post and Cubist Geometries.)
Comments Off on Defining Form (continued)
Tuesday, January 10, 2012
Defining Form
(Continued from Epiphany and from yesterday.)
Detail from the current American Mathematical Society homepage—
Further detail, with a comparison to Dürer’s magic square—
 |
 |
The three interpenetrating planes in the foreground of Donmoyer‘s picture
provide a clue to the structure of the the magic square array behind them.
Group the 16 elements of Donmoyer’s array into four 4-sets corresponding to the
four rows of Dürer’s square, and apply the 4-color decomposition theorem.
Note the symmetry of the set of 3 line diagrams that result.
Now consider the 4-sets 1-4, 5-8, 9-12, and 13-16, and note that these
occupy the same positions in the Donmoyer square that 4-sets of
like elements occupy in the diamond-puzzle figure below—
Thus the Donmoyer array also enjoys the structural symmetry,
invariant under 322,560 transformations, of the diamond-puzzle figure.
Just as the decomposition theorem’s interpenetrating lines explain the structure
of a 4×4 square , the foreground’s interpenetrating planes explain the structure
of a 2x2x2 cube .
For an application to theology, recall that interpenetration is a technical term
in that field, and see the following post from last year—
| Saturday, June 25, 2011
— m759 @ 12:00 PM “… the formula ‘Three Hypostases in one Ousia ‘
Ousia
|
Comments Off on Defining Form
Saturday, February 27, 2010
Cubist Geometries
"The cube has…13 axes of symmetry:
6 C2 (axes joining midpoints of opposite edges),
4 C3 (space diagonals), and
3C4 (axes joining opposite face centroids)."
–Wolfram MathWorld article on the cube
These 13 symmetry axes can be used to illustrate the interplay between Euclidean and Galois geometry in a cubic model of the 13-point Galois plane.
The geometer's 3×3×3 cube–
27 separate subcubes unconnected
by any Rubik-like mechanism–
The 13 symmetry axes of the (Euclidean) cube–
exactly one axis for each pair of opposite
subcubes in the (Galois) 3×3×3 cube–
A closely related structure–
the finite projective plane
with 13 points and 13 lines–
A later version of the 13-point plane
by Ed Pegg Jr.–
A group action on the 3×3×3 cube
as illustrated by a Wolfram program
by Ed Pegg Jr. (undated, but closely
related to a March 26, 1985 note
by Steven H. Cullinane)–
The above images tell a story of sorts.
The moral of the story–
Galois projective geometries can be viewed
in the context of the larger affine geometries
from which they are derived.
The standard definition of points in a Galois projective plane is that they are lines through the (arbitrarily chosen) origin in a corresponding affine 3-space converted to a vector 3-space.
If we choose the origin as the center cube in coordinatizing the 3×3×3 cube (See Weyl's relativity problem ), then the cube's 13 axes of symmetry can, if the other 26 cubes have properly (Weyl's "objectively") chosen coordinates, illustrate nicely the 13 projective points derived from the 27 affine points in the cube model.
The 13 lines of the resulting Galois projective plane may be derived from Euclidean planes through the cube's center point that are perpendicular to the cube's 13 Euclidean symmetry axes.
The above standard definition of points in a Galois projective plane may of course also be used in a simpler structure– the eightfold cube.
(The eightfold cube also allows a less standard way to picture projective points that is related to the symmetries of "diamond" patterns formed by group actions on graphic designs.)
See also Ed Pegg Jr. on finite geometry on May 30, 2006
at the Mathematical Association of America.
Comments Off on Cubist Geometries
Thursday, February 5, 2009
Thursday February 5, 2009
Through the
Looking Glass:
A Sort of Eternity
From the new president’s inaugural address:
“… in the words of Scripture, the time has come to set aside childish things.”
The words of Scripture:
“through a glass”—
[di’ esoptrou].
By means of
a mirror [esoptron].
Childish things:
© 2005 The Institute for Figuring
Photo by Norman Brosterman
fom the Inventing Kindergarten
exhibit at The Institute for Figuring
(co-founded by Margaret Wertheim)
fom the Inventing Kindergarten
exhibit at The Institute for Figuring
(co-founded by Margaret Wertheim)
Not-so-childish:
Three planes through
the center of a cube
that split it into
eight subcubes:
Through a glass, darkly:
A group of 8 transformations is
generated by affine reflections
in the above three planes.
Shown below is a pattern on
the faces of the 2x2x2 cube
that is symmetric under one of
these 8 transformations–
a 180-degree rotation:
(Click on image
for further details.)
But then face to face:
A larger group of 1344,
rather than 8, transformations
of the 2x2x2 cube
is generated by a different
sort of affine reflections– not
in the infinite Euclidean 3-space
over the field of real numbers,
but rather in the finite Galois
3-space over the 2-element field.
Galois age fifteen,
drawn by a classmate.
These transformations
in the Galois space with
finitely many points
produce a set of 168 patterns
like the one above.
For each such pattern,
at least one nontrivial
transformation in the group of 8
described above is a symmetry
in the Euclidean space with
infinitely many points.
For some generalizations,
see Galois Geometry.
Related material:
The central aim of Western religion–
"Each of us has something to offer the Creator... the bridging of masculine and feminine, life and death. It's redemption.... nothing else matters." -- Martha Cooley in The Archivist (1998) The central aim of Western philosophy– Dualities of Pythagoras as reconstructed by Aristotle: Limited Unlimited Odd Even Male Female Light Dark Straight Curved ... and so on .... “Of these dualities, the first is the most important; all the others may be seen as different aspects of this fundamental dichotomy. To establish a rational and consistent relationship between the limited [man, etc.] and the unlimited [the cosmos, etc.] is… the central aim of all Western philosophy.” — Jamie James in The Music of the Spheres (1993) “In the garden of Adding — The Midrash Jazz Quartet in City of God, by E. L. Doctorow (2000) A quotation today at art critic Carol Kino’s website, slightly expanded: “Art inherited from the old religion — Octavio Paz,”Seeing and Using: Art and Craftsmanship,” in Convergences: Essays on Art and Literature (New York: Harcourt Brace Jovanovich 1987), 52 From Brian O’Doherty’s 1976 Artforum essays– not on museums, but rather on gallery space: “We have now reached
“Space: what you — James Joyce, Ulysses |
Comments Off on Thursday February 5, 2009
Tuesday, October 3, 2006
Tuesday October 3, 2006
Serious
"I don't think the 'diamond theorem' is anything serious, so I started with blitzing that."
— Charles Matthews at Wikipedia, Oct. 2, 2006
"The 'seriousness' of a mathematical theorem lies, not in its practical consequences, which are usually negligible, but in the significance of the mathematical ideas which it connects. We may say, roughly, that a mathematical idea is 'significant' if it can be connected, in a natural and illuminating way, with a large complex of other mathematical ideas."
— G. H. Hardy, A Mathematician's Apology
Matthews yesterday deleted references to the diamond theorem and related material in the following Wikipedia articles:
Affine group
Reflection group
Symmetry in mathematics
Incidence structure
Invariant (mathematics)
Symmetry
Finite geometry
Group action
History of geometry
This would appear to be a fairly large complex of mathematical ideas.
See also the following "large complex" cited, following the above words of Hardy, in Diamond Theory:
Affine geometry, affine planes, affine spaces, automorphisms, binary codes, block designs, classical groups, codes, coding theory, collineations, combinatorial, combinatorics, conjugacy classes, the Conwell correspondence, correlations, design theory, duads, duality, error correcting codes, exceptional groups, finite fields, finite geometry, finite groups, finite rings, Galois fields, generalized quadrangles, generators, geometry, GF(2), GF(4), the (24,12) Golay code, group actions, group theory, Hadamard matrices, hypercube, hyperplanes, hyperspace, incidence structures, invariance, Karnaugh maps, Kirkman's schoolgirl problem, Latin squares, Leech lattice, linear groups, linear spaces, linear transformations, Mathieu groups, matrix theory, Meno, Miracle Octad Generator, MOG, multiply transitive groups, octads, the octahedral group, orthogonal arrays, outer automorphisms, parallelisms, partial geometries, permutation groups, PG(3,2), polarities, Polya-Burnside theorem, projective geometry, projective planes, projective spaces, projectivities, Reed-Muller codes, the relativity problem, Singer cycle, skew lines, sporadic simple groups, Steiner systems, symmetric, symmetry, symplectic, synthemes, synthematic, tesseract, transvections, Walsh functions, Witt designs.
Comments Off on Tuesday October 3, 2006
Wednesday, May 4, 2005
Wednesday May 4, 2005
The Fano Plane
Revisualized:
Revisualized:
or, The Eightfold Cube
Here is the usual model of the seven points and seven lines (including the circle) of the smallest finite projective plane (the Fano plane):
Every permutation of the plane's points that preserves collinearity is a symmetry of the plane. The group of symmetries of the Fano plane is of order 168 and is isomorphic to the group PSL(2,7) = PSL(3,2) = GL(3,2). (See Cameron on linear groups (pdf).)
The above model indicates with great clarity six symmetries of the plane– those it shares with the equilateral triangle. It does not, however, indicate where the other 162 symmetries come from.
Shown below is a new model of this same projective plane, using partitions of cubes to represent points:
The cubes' partitioning planes are added in binary (1+1=0) fashion. Three partitioned cubes are collinear if and only if their partitioning planes' binary sum equals zero.
The second model is useful because it lets us generate naturally all 168 symmetries of the Fano plane by splitting a cube into a set of four parallel 1x1x2 slices in the three ways possible, then arbitrarily permuting the slices in each of the three sets of four. See examples below.
For a proof that such permutations generate the 168 symmetries, see Binary Coordinate Systems.
(Note that this procedure, if regarded as acting on the set of eight individual subcubes of each cube in the diagram, actually generates a group of 168*8 = 1,344 permutations. But the group's action on the diagram's seven partitions of the subcubes yields only 168 distinct results. This illustrates the difference between affine and projective spaces over the binary field GF(2). In a related 2x2x2 cubic model of the affine 3-space over GF(2) whose "points" are individual subcubes, the group of eight translations is generated by interchanges of parallel 2x2x1 cube-slices. This is clearly a subgroup of the group generated by permuting 1x1x2 cube-slices. Such translations in the affine 3-space have no effect on the projective plane, since they leave each of the plane model's seven partitions– the "points" of the plane– invariant.)
To view the cubes model in a wider context, see Galois Geometry, Block Designs, and Finite-Geometry Models.
For another application of the points-as-partitions technique, see Latin-Square Geometry: Orthogonal Latin Squares as Skew Lines.
For more on the plane's symmetry group in another guise, see John Baez on Klein's Quartic Curve and the online book The Eightfold Way. For more on the mathematics of cubic models, see Solomon's Cube.
For a large downloadable folder with many other related web pages, see Notes on Finite Geometry.
Comments Off on Wednesday May 4, 2005