See the title in this journal.
https://www.google.com/search?q="in+terms+of+combinational+delight"
Tuesday, June 11, 2024
A Smooth Process . . . Indiscrete Rota
Comments Off on A Smooth Process . . . Indiscrete Rota
Friday, August 14, 2015
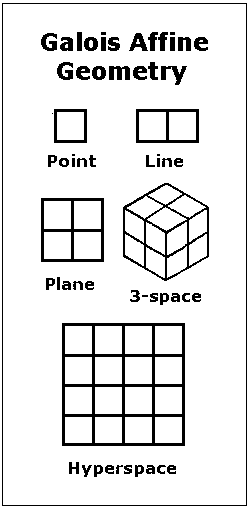
Discrete Space
(A review)
Galois space:
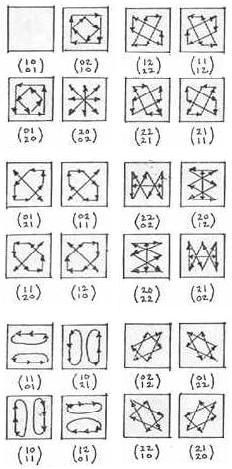
Counting symmetries of Galois space:
The reason for these graphic symmetries in affine Galois space —
symmetries of the underlying projective Galois space:
Comments Off on Discrete Space
Monday, April 10, 2023
Space
(Perspective Not as Symbolic Form)
From a post of June 8, 2014 —
See August 6, 2013 — Desargues via Galois.
Comments Off on Space
Sunday, January 22, 2023
The Stillwell Dichotomies
| Number | Space |
| Arithmetic | Geometry |
| Discrete | Continuous |
Related literature —
From a "Finite Fields in 1956" post —
The Nutshell:
Related Narrative:
Comments Off on The Stillwell Dichotomies
Tuesday, September 13, 2022
A Helpful Survey of the Literature
Some background for the exercise of 9/11 —
Vera Pless, "More on the uniqueness of the Golay codes,"
Discrete Mathematics 106/107 (1992) 391-398 —
"Several people [1-2,6] have shown that
any set of 212 binary vectors of length 24,
distance ≥ 8, containing 0, must be the
unique (up to equivalence) [24,12,8] Golay code."
[1] P. Delsarte and J.M. Goethals, "Unrestricted codes
with the Golay parameters are unique,"
Discrete Math. 12 (1975) 211-224.
[2] A. Neumeier, private communication, 1990.
[6] S.L. Snover, "The uniqueness of the
Nordstrom-Robinson and the Golay binary codes,"
Ph.D. Thesis, Dept. of Mathematics,
Michigan State Univ., 1973.
Related images —
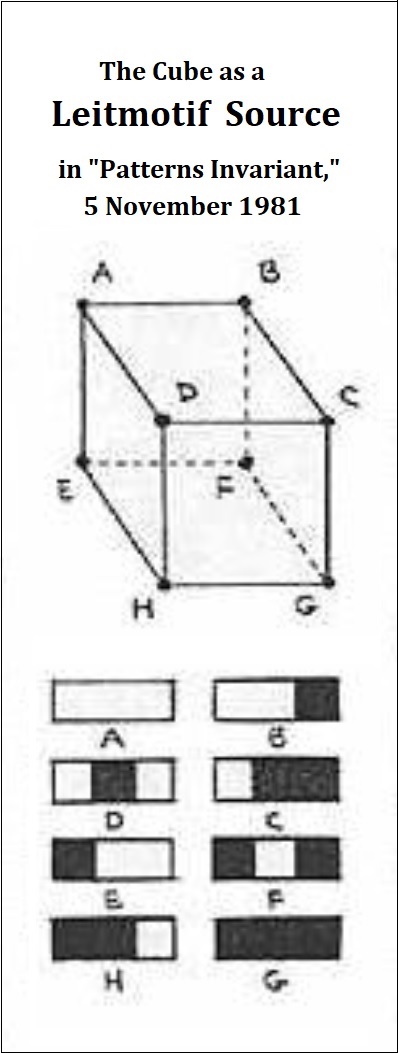
"Before time began, there was the Cube."
"Remember, remember the fifth of November"
Comments Off on A Helpful Survey of the Literature
Sunday, May 21, 2017
Rota on Beauty
Tiptoe through the tulips with Rota and Erickson:
|
Attempts have been made to string together beautiful mathematical results and to present them in books bearing such attractive titles as The One Hundred Most Beautiful Theorems of Mathematics. Such anthologies are seldom found on a mathematician’s bookshelf. The beauty of a theorem is best observed when the theorem is presented as the crown jewel within the context of a theory. — Gian-Carlo Rota in Indiscrete Thoughts |
See also Martin Erickson in this journal . . .
Comments Off on Rota on Beauty
Wednesday, April 12, 2017
Expanding the Spielraum
"Cézanne ignores the laws of classical perspective . . . ."
— Voorhies, James. “Paul Cézanne (1839–1906).”
In Heilbrunn Timeline of Art History . New York:
The Metropolitan Museum of Art, 2000–. (October 2004)
Some others do not.
This is what I called "the large Desargues configuration"
in posts of April 2013 and later.
Comments Off on Expanding the Spielraum
Thursday, August 11, 2016
The Large Desargues Configuration
(Continued from April 2013 and later)
This is what I called "the large Desargues configuration"
in posts of April 2013 and later.
Comments Off on The Large Desargues Configuration
Friday, November 27, 2015
Einstein and Geometry
(A Prequel to Dirac and Geometry)
"So Einstein went back to the blackboard.
And on Nov. 25, 1915, he set down
the equation that rules the universe.
As compact and mysterious as a Viking rune,
it describes space-time as a kind of sagging mattress…."
— Dennis Overbye in The New York Times online,
November 24, 2015
Some pure mathematics I prefer to the sagging Viking mattress —
Readings closely related to the above passage —
Thomas Hawkins, "From General Relativity to Group Representations:
the Background to Weyl's Papers of 1925-26," in Matériaux pour
l'histoire des mathématiques au XXe siècle: Actes du colloque
à la mémoire de Jean Dieudonné, Nice, 1996 (Soc. Math.
de France, Paris, 1998), pp. 69-100.
The 19th-century algebraic theory of invariants is discussed
as what Weitzenböck called a guide "through the thicket
of formulas of general relativity."
Wallace Givens, "Tensor Coordinates of Linear Spaces," in
Annals of Mathematics Second Series, Vol. 38, No. 2, April 1937,
pp. 355-385.
Tensors (also used by Einstein in 1915) are related to
the theory of line complexes in three-dimensional
projective space and to the matrices used by Dirac
in his 1928 work on quantum mechanics.
For those who prefer metaphors to mathematics —
Rota fails to cite the source of his metaphor.
|
Comments Off on Einstein and Geometry
Saturday, May 26, 2012
Harriot’s Cubes
See also Finite Geometry and Physical Space.
Related material from MacTutor—
The paper by J. W. Shirley, Binary numeration before Leibniz, Amer. J. Physics 19 (8) (1951), 452-454, contains an interesting look at some mathematics which appears in the hand written papers of Thomas Harriot [1560-1621]. Using the photographs of the two original Harriot manuscript pages reproduced in Shirley’s paper, we explain how Harriot was doing arithmetic with binary numbers. Leibniz [1646-1716] is credited with the invention [1679-1703] of binary arithmetic, that is arithmetic using base 2. Laplace wrote:-
However, Leibniz was certainly not the first person to think of doing arithmetic using numbers to base 2. Many years earlier Harriot had experimented with the idea of different number bases…. |
For a discussion of Harriot on the discrete-vs.-continuous question,
see Katherine Neal, From Discrete to Continuous: The Broadening
of Number Concepts in Early Modern England (Springer, 2002),
pages 69-71.
Comments Off on Harriot’s Cubes
Saturday, April 28, 2012
Sprechen Sie Deutsch?
A Log24 post, "Bridal Birthday," one year ago today linked to
"The Discrete and the Continuous," a brief essay by David Deutsch.
From that essay—
"The idea of quantization—
the discreteness of physical quantities—
turned out to be immensely fruitful."
Deutsch's "idea of quantization" also appears in
the April 12 Log24 post Mythopoetic—
|
"Is Space Digital?" — Cover story, Scientific American "The idea that space may be digital — Physicist Sabine Hossenfelder "A quantization of space/time — Peter Woit in a comment |
It seems some clarification is in order.
Hossenfelder's "The idea that space may be digital"
and Woit's "a quantization of space/time" may not
refer to the same thing.
Scientific American on the concept of digital space—
"Space may not be smooth and continuous.
Instead it may be digital, composed of tiny bits."
Wikipedia on the concept of quantization—
Causal sets, loop quantum gravity, string theory,
and black hole thermodynamics all predict
a quantized spacetime….
For a purely mathematical approach to the
continuous-vs.-discrete issue, see
Finite Geometry and Physical Space.
The physics there is somewhat tongue-in-cheek,
but the geometry is serious.The issue there is not
continuous-vs.-discrete physics , but rather
Euclidean-vs.-Galois geometry .
Both sorts of geometry are of course valid.
Euclidean geometry has long been applied to
physics; Galois geometry has not. The cited
webpage describes the interplay of both sorts
of geometry— Euclidean and Galois, continuous
and discrete— within physical space— if not
within the space of physics.
Comments Off on Sprechen Sie Deutsch?
Wednesday, March 21, 2012
Digital Theology
See also remarks on Digital Space and Digital Time in this journal.
Such remarks can, of course, easily verge on crackpot territory.
For some related pure mathematics, see Symmetry of Walsh Functions.
Comments Off on Digital Theology
Thursday, April 28, 2011
Bridal Birthday
Catherine Elizabeth "Kate" Middleton, born 9 January 1982,
will marry Prince William of Wales on April 29th, 2011.
This suggests, by a very illogical and roundabout process
of verbal association, a search in this journal.
A quote from that search—
“‘Memory is non-narrative and non-linear.’
— Maya Lin in The Harvard Crimson , Friday, Dec. 2, 2005
A non-narrative image from the same
general time span as the bride's birthday—
For some context, see Stevens + "The Rock" + "point A".
A post in that search, April 4th's Rock Notes, links to an essay
on physics and philosophy, "The Discrete and the Continuous," by David Deutsch.
See also the article on Deutsch, "Dream Machine," in the current New Yorker
(May 2, 2011), and the article's author, "Rivka Galchen," in this journal.
Galchen writes very well. For example —
| Galchen on quantum theory—
"Our intuition, going back forever, is that to move, say, a rock, one has to touch that rock, or touch a stick that touches the rock, or give an order that travels via vibrations through the air to the ear of a man with a stick that can then push the rock—or some such sequence. This intuition, more generally, is that things can only directly affect other things that are right next to them. If A affects B without being right next to it, then the effect in question must be in direct—the effect in question must be something that gets transmitted by means of a chain of events in which each event brings about the next one directly, in a manner that smoothly spans the distance from A to B. Every time we think we can come up with an exception to this intuition—say, flipping a switch that turns on city street lights (but then we realize that this happens through wires) or listening to a BBC radio broadcast (but then we realize that radio waves propagate through the air)—it turns out that we have not, in fact, thought of an exception. Not, that is, in our everyday experience of the world. We term this intuition 'locality.' Quantum mechanics has upended many an intuition, but none deeper than this one." |
Comments Off on Bridal Birthday
Tuesday, November 23, 2010
Art Object
There is more than one way
to look at a cube.
From Cambridge U. Press on Feb. 20, 2006 —
and from this journal on June 30, 2010 —
In memory of Wu Guanzhong, Chinese artist
who died in Beijing on June 25, 2010 —
See also this journal on Feb. 20, 2006
(the day The Cube was published).
Comments Off on Art Object
Sunday, September 2, 2007
Sunday September 2, 2007
Comment at the
n-Category Cafe
Re: This Week’s Finds in Mathematical Physics (Week 251)
On Spekkens’ toy system and finite geometry
Background–
- In “Week 251” (May 5, 2007), John wrote:
“Since Spekkens’ toy system resembles a qubit, he calls it a “toy bit”. He goes on to study systems of several toy bits – and the charming combinatorial geometry I just described gets even more interesting. Alas, I don’t really understand it well: I feel there must be some mathematically elegant way to describe it all, but I don’t know what it is…. All this is fascinating. It would be nice to find the mathematical structure that underlies this toy theory, much as the category of Hilbert spaces underlies honest quantum mechanics.” - In the n-Category Cafe ( May 12, 2007, 12:26 AM, ) Matt Leifer wrote:
“It’s crucial to Spekkens’ constructions, and particularly to the analog of superposition, that the state-space is discrete. Finding a good mathematical formalism for his theory (I suspect finite fields may be the way to go) and placing it within a comprehensive framework for generalized theories would be very interesting.” - In the n-category Cafe ( May 12, 2007, 6:25 AM) John Baez wrote:
“Spekkens and I spent an afternoon trying to think about his theory as quantum mechanics over some finite field, but failed — we almost came close to proving it couldnt’ work.”
On finite geometry:
- In “Week 234” (June 12, 2006), John wrote:
“For a pretty explanation of M24… try this:
… Steven H. Cullinane, Geometry of the 4 × 4 square,
http://finitegeometry.org/sc/16/geometry.html”
The actions of permutations on a 4 × 4 square in Spekkens’ paper (quant-ph/0401052), and Leifer’s suggestion of the need for a “generalized framework,” suggest that finite geometry might supply such a framework. The geometry in the webpage John cited is that of the affine 4-space over the two-element field.
Related material:
Update of
Sept. 5, 2007
Sept. 5, 2007
See also arXiv:0707.0074v1 [quant-ph], June 30, 2007:
A fully epistemic model for a local hidden variable emulation of quantum dynamics,
by Michael Skotiniotis, Aidan Roy, and Barry C. Sanders, Institute for Quantum Information Science, University of Calgary. Abstract: "In this article we consider an augmentation of Spekkens’ toy model for the epistemic view of quantum states [1]…."
Skotiniotis et al. note that the group actions on the 4×4 square described in Spekkens' paper [1] may be viewed (as in Geometry of the 4×4 Square and Geometry of Logic) in the context of a hypercube, or tesseract, a structure in which adjacency is isomorphic to adjacency in the 4 × 4 square (on a torus).
Hypercube from the Skotiniotis paper:
Reference:
[1] Robert W. Spekkens, Phys. Rev. A 75, 032110 (2007),
Evidence for the epistemic view of quantum states: A toy theory,
Evidence for the epistemic view of quantum states: A toy theory,
Perimeter Institute for Theoretical Physics, 31 Caroline Street North, Waterloo, Ontario, Canada N2L 2Y5 (Received 11 October 2005; revised 2 November 2006; published 19 March 2007.)
Comments Off on Sunday September 2, 2007
Tuesday, February 20, 2007
Tuesday February 20, 2007
Symmetry
Today is the 21st birthday of my note “The Relativity Problem in Finite Geometry.”
Some relevant quotations:
“This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them.”
— Hermann Weyl, The Classical Groups, Princeton University Press, 1946, p. 16
Describing the branch of mathematics known as Galois theory, Weyl says that it
“… is nothing else but the relativity theory for the set Sigma, a set which, by its discrete and finite character, is conceptually so much simpler than the infinite set of points in space or space-time dealt with by ordinary relativity theory.”
— Weyl, Symmetry, Princeton University Press, 1952, p. 138
Weyl’s set Sigma is a finite set of complex numbers. Some other sets with “discrete and finite character” are those of 4, 8, 16, or 64 points, arranged in squares and cubes. For illustrations, see Finite Geometry of the Square and Cube. What Weyl calls “the relativity problem” for these sets involves fixing “objectively” a class of equivalent coordinatizations. For what Weyl’s “objectively” means, see the article “Symmetry and Symmetry Breaking,” by Katherine Brading and Elena Castellani, in the Stanford Encyclopedia of Philosophy:
“The old and natural idea that what is objective should not depend upon the particular perspective under which it is taken into consideration is thus reformulated in the following group-theoretical terms: what is objective is what is invariant with respect to the transformation group of reference frames, or, quoting Hermann Weyl (1952, p. 132), ‘objectivity means invariance with respect to the group of automorphisms [of space-time].‘[22]
22. The significance of the notion of invariance and its group-theoretic treatment for the issue of objectivity is explored in Born (1953), for example. For more recent discussions see Kosso (2003) and Earman (2002, Sections 6 and 7).
References:
Born, M., 1953, “Physical Reality,” Philosophical Quarterly, 3, 139-149. Reprinted in E. Castellani (ed.), Interpreting Bodies: Classical and Quantum Objects in Modern Physics, Princeton, NJ: Princeton University Press, 1998, pp. 155-167.
Earman, J., 2002, “Laws, Symmetry, and Symmetry Breaking; Invariance, Conservation Principles, and Objectivity,’ PSA 2002, Proceedings of the Biennial Meeting of the Philosophy of Science Association 2002, forthcoming [Abstract/Preprint available online]
Kosso, P., 2003, “Symmetry, objectivity, and design,” in K. Brading and E. Castellani (eds.), Symmetries in Physics: Philosophical Reflections, Cambridge: Cambridge University Press, pp. 410-421.
Weyl, H., 1952, Symmetry, Princeton, NJ: Princeton University Press.
See also
Archives Henri Poincaré (research unit UMR 7117, at Université Nancy 2, of the CNRS)–
“Minkowski, Mathematicians, and the Mathematical Theory of Relativity,” by Scott Walter, in The Expanding Worlds of General Relativity (Einstein Studies, volume 7), H. Goenner, J. Renn, J. Ritter and T. Sauer, editors, Boston/Basel: Birkhäuser, 1999, pp. 45-86–
“Developing his ideas before Göttingen mathematicians in April 1909, Klein pointed out that the new theory based on the Lorentz group (which he preferred to call ‘Invariantentheorie’) could have come from pure mathematics (1910: 19). He felt that the new theory was anticipated by the ideas on geometry and groups that he had introduced in 1872, otherwise known as the Erlangen program (see Gray 1989: 229).”
References:
Gray, Jeremy J. (1989). Ideas of Space. 2d ed. Oxford: Oxford University Press.
Klein, Felix. (1910). “Über die geometrischen Grundlagen der Lorentzgruppe.” Jahresbericht der deutschen Mathematiker-Vereinigung 19: 281-300. [Reprinted: Physikalische Zeitschrift 12 (1911): 17-27].
Related material: A pathetically garbled version of the above concepts was published in 2001 by Harvard University Press. See Invariances: The Structure of the Objective World, by Robert Nozick.
Comments Off on Tuesday February 20, 2007
Friday, October 20, 2006
Friday October 20, 2006
“At present, such relationships can
at best be heuristically described
in terms that invoke some notion
of an ‘intelligent user standing
outside the system.'”
at best be heuristically described
in terms that invoke some notion
of an ‘intelligent user standing
outside the system.'”
— Gian-Carlo Rota in
Indiscrete Thoughts, p. 152
Related Material
The Devil’s Bible and
Nothing Nothings (Again).
The Context
One context for the Rota quote
is Paul Halmos’s remark, quoted
in today’s New York Times,
that mathematics is
“almost like being
in touch with God.”
Another context is
Log24 on Aug. 29, 2005.
Comments Off on Friday October 20, 2006
Monday, August 29, 2005
Monday August 29, 2005
| Date: Sun, 28 Aug 2005 12:30:40 -0400 From: Alf van der Poorten AM Subject: Vale George Szekeres and Esther Klein Szekeres Members of the Number Theory List will be sad to learn that George and Esther Szekeres both died this morning. George, 94, had been quite ill for the last 2-3 days, barely conscious, and died first at 06:30. Esther, 95, died a half hour later. Both George Szekeres and Esther Klein will be recalled by number theorists as members of the group of young Hungarian mathematicians of the 1930s including Turan and Erdos. George and Esther's coming to Australia in the late 40s played an important role in the invigoration of Australian Mathematics. George was also an expert in group theory and relativity; he was my PhD supervisor. Emeritus Professor |
Related material:
AVE
| "Hello! Kinch here. Put me on to Edenville. Aleph, alpha: nought, nought, one."
"A very short space of time through very short times of space…. — James Joyce, Ulysses, Proteus chapter A very short space of time through very short times of space…. "It is demonstrated that space-time should possess a discrete structure on Planck scales." — Peter Szekeres, abstract of Discrete Space-Time |
Peter Szekeres is the son of George and Esther Szekeres.
ATQUE
"At present, such relationships can at best be heuristically described in terms that invoke some notion of an 'intelligent user standing outside the system.'"
— Gian-Carlo Rota in Indiscrete Thoughts, p. 152
Comments Off on Monday August 29, 2005
Thursday, August 25, 2005
Thursday August 25, 2005
Analogical
Train of Thought
From S. H. Cullinane,
Visualizing GL(2,p),
March 26, 1985–
Train of Thought
Part I: The 24-Cell
From S. H. Cullinane,
Visualizing GL(2,p),
March 26, 1985–
| From John Baez, “This Week’s Finds in Mathematical Physics (Week 198),” September 6, 2003: Noam Elkies writes to John Baez:
The enrapturing discoveries of our field systematically conceal, like footprints erased in the sand, the analogical train of thought that is the authentic life of mathematics – Gian-Carlo Rota |
Like footprints erased in the sand….
Part II: Discrete Space
“Hello! Kinch here. Put me on to Edenville. Aleph, alpha: nought, nought, one.”
“A very short space of time through very short times of space….
Am I walking into eternity along Sandymount strand?”
— James Joyce, Ulysses, Proteus chapter
A very short space of time through very short times of space….
“It is demonstrated that space-time should possess a discrete structure on Planck scales.”
— Peter Szekeres, abstract of Discrete Space-Time
“A theory…. predicts that space and time are indeed made of discrete pieces.”
— Lee Smolin in Atoms of Space and Time (pdf), Scientific American, Jan. 2004
“… a fundamental discreteness of spacetime seems to be a prediction of the theory….”
— Thomas Thiemann, abstract of Introduction to Modern Canonical Quantum General Relativity
“Theories of discrete space-time structure are being studied from a variety of perspectives.”
— Quantum Gravity and the Foundations of Quantum Mechanics at Imperial College, London
Disclaimer:
The above speculations by physicists
are offered as curiosities.
I have no idea whether
any of them are correct.
Related material:
Stephen Wolfram offers a brief
History of Discrete Space.
For a discussion of space as discrete
by a non-physicist, see John Bigelow‘s
Space and Timaeus.
Part III: Quaternions
in a Discrete Space
in a Discrete Space
Apart from any considerations of
physics, there are of course many
purely mathematical discrete spaces.
See Visible Mathematics, continued
(Aug. 4, 2005):
physics, there are of course many
purely mathematical discrete spaces.
See Visible Mathematics, continued
(Aug. 4, 2005):
Comments Off on Thursday August 25, 2005
Saturday, June 4, 2005
Saturday June 4, 2005
Drama of the Diagonal
The 4×4 Square:
French Perspectives
The 4×4 Square:
French Perspectives
Earendil_Silmarils:
Les Anamorphoses:
"Pour construire un dessin en perspective,
le peintre trace sur sa toile des repères:
la ligne d'horizon (1),
le point de fuite principal (2)
où se rencontre les lignes de fuite (3)
et le point de fuite des diagonales (4)."
_______________________________
Serge Mehl,
Perspective &
Géométrie Projective:
"… la géométrie projective était souvent
synonyme de géométrie supérieure.
Elle s'opposait à la géométrie
euclidienne: élémentaire…
La géométrie projective, certes supérieure
car assez ardue, permet d'établir
de façon élégante des résultats de
la géométrie élémentaire."
Similarly…
Finite projective geometry
(in particular, Galois geometry)
is certainly superior to
the elementary geometry of
quilt-pattern symmetry
and allows us to establish
de façon élégante
some results of that
elementary geometry.
Other Related Material…
from algebra rather than
geometry, and from a German
rather than from the French:
"This is the relativity problem:
to fix objectively a class of
equivalent coordinatizations
and to ascertain
the group of transformations S
mediating between them."
— Hermann Weyl,
The Classical Groups,
Princeton U. Press, 1946
Evariste Galois
Weyl also says that the profound branch
of mathematics known as Galois theory
"… is nothing else but the
relativity theory for the set Sigma,
a set which, by its discrete and
finite character, is conceptually
so much simpler than the
infinite set of points in space
or space-time dealt with
by ordinary relativity theory."
— Weyl, Symmetry,
Princeton U. Press, 1952
Metaphor and Algebra…
relativity theory for the set Sigma,
a set which, by its discrete and
finite character, is conceptually
so much simpler than the
infinite set of points in space
or space-time dealt with
by ordinary relativity theory."
— Weyl, Symmetry,
Princeton U. Press, 1952
Metaphor and Algebra…
"Perhaps every science must
start with metaphor
and end with algebra;
and perhaps without metaphor
there would never have been
any algebra."
— attributed, in varying forms, to
Max Black, Models and Metaphors, 1962
Max Black, Models and Metaphors, 1962
For metaphor and
algebra combined, see
"Symmetry invariance
in a diamond ring,"
in a diamond ring,"
A.M.S. abstract 79T-A37,
Notices of the
American Mathematical Society,
February 1979, pages A-193, 194 —
the original version of the 4×4 case
of the diamond theorem.
More on Max Black…
"When approaching unfamiliar territory, we often, as observed earlier, try to describe or frame the novel situation using metaphors based on relations perceived in a familiar domain, and by using our powers of association, and our ability to exploit the structural similarity, we go on to conjecture new features for consideration, often not noticed at the outset. The metaphor works, according to Max Black, by transferring the associated ideas and implications of the secondary to the primary system, and by selecting, emphasising and suppressing features of the primary in such a way that new slants on it are illuminated."
— Paul Thompson, University College, Oxford,
The Nature and Role of Intuition
in Mathematical Epistemology
A New Slant…
That intuition, metaphor (i.e., analogy), and association may lead us astray is well known. The examples of French perspective above show what might happen if someone ignorant of finite geometry were to associate the phrase "4×4 square" with the phrase "projective geometry." The results are ridiculously inappropriate, but at least the second example does, literally, illuminate "new slants"– i.e., diagonals– within the perspective drawing of the 4×4 square.
Similarly, analogy led the ancient Greeks to believe that the diagonal of a square is commensurate with the side… until someone gave them a new slant on the subject.
Comments Off on Saturday June 4, 2005
Friday, February 20, 2004
Friday February 20, 2004
Finite Relativity
Today is the 18th birthday of my note
“The Relativity Problem in Finite Geometry.”
That note begins with a quotation from Weyl:
“This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them.”
— Hermann Weyl, The Classical Groups, Princeton University Press, 1946, p. 16
Here is another quotation from Weyl, on the profound branch of mathematics known as Galois theory, which he says
“… is nothing else but the relativity theory for the set Sigma, a set which, by its discrete and finite character, is conceptually so much simpler than the infinite set of points in space or space-time dealt with by ordinary relativity theory.”
— Weyl, Symmetry, Princeton University Press, 1952, p. 138
This second quotation applies equally well to the much less profound, but more accessible, part of mathematics described in Diamond Theory and in my note of Feb. 20, 1986.
Saturday, November 1, 2003
Saturday November 1, 2003
Symmetry in Diamond Theory:
Robbing Peter to Pay Paul
"Groups arise in most areas of pure and applied mathematics, usually as a set of operators or transformations of some structure. The appearance of a group generally reflects some kind of symmetry in the object under study, and such symmetry may be considered one of the fundamental notions of mathematics."
"Counter-change is sometimes known as Robbing Peter to Pay Paul."
|
|
|
|
Paul Robeson in |
For a look at the Soviet approach
to counterchange symmetry, see
The Kishinev School of Discrete Geometry.
The larger cultural context:
See War of Ideas (Oct. 24),
The Hunt for Red October (Oct. 25),
On the Left (Oct. 25), and
ART WARS for Trotsky's Birthday (Oct. 26).