From Ursula K. Le Guin’s novel
The Dispossessed: An Ambiguous Utopia (1974)—
Chapter One
“There was a wall. It did not look important. It was built of uncut rocks roughly mortared. An adult could look right over it, and even a child could climb it. Where it crossed the roadway, instead of having a gate it degenerated into mere geometry, a line, an idea of boundary. But the idea was real. It was important. For seven generations there had been nothing in the world more important than that wall.
Like all walls it was ambiguous, two-faced. What was inside it and what was outside it depended upon which side of it you were on.”
Note—
“We note that the phrase ‘instead of having a gate it degenerated into mere geometry’ is mere fatuousness. If there is an idea here, degenerate, mere, and geometry in concert do not fix it. They bat at it like a kitten at a piece of loose thread.”
— Samuel R. Delany, The Jewel-Hinged Jaw: Notes on the Language of Science Fiction (Dragon Press, 1977), page 110 of revised edition, Wesleyan University Press, 2009
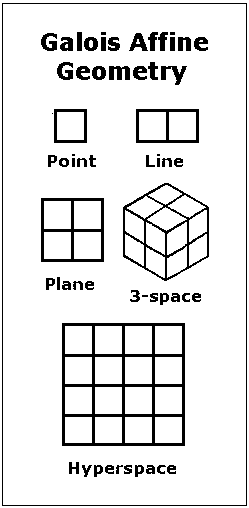
(For the phrase mere geometry elsewhere, see a note of April 22. The apparently flat figures in that note’s illustration “Galois Affine Geometry” may be regarded as degenerate views of cubes.)
Later in the Le Guin novel—
“… The Terrans had been intellectual imperialists, jealous wall builders. Even Ainsetain, the originator of the theory, had felt compelled to give warning that his physics embraced no mode but the physical and should not be taken as implying the metaphysical, the philosophical, or the ethical. Which, of course, was superficially true; and yet he had used number, the bridge between the rational and the perceived, between psyche and matter, ‘Number the Indisputable,’ as the ancient founders of the Noble Science had called it. To employ mathematics in this sense was to employ the mode that preceded and led to all other modes. Ainsetain had known that; with endearing caution he had admitted that he believed his physics did, indeed, describe reality.
Strangeness and familiarity: in every movement of the Terran’s thought Shevek caught this combination, was constantly intrigued. And sympathetic: for Ainsetain, too, had been after a unifying field theory. Having explained the force of gravity as a function of the geometry of spacetime, he had sought to extend the synthesis to include electromagnetic forces. He had not succeeded. Even during his lifetime, and for many decades after his death, the physicists of his own world had turned away from his effort and its failure, pursuing the magnificent incoherences of quantum theory with its high technological yields, at last concentrating on the technological mode so exclusively as to arrive at a dead end, a catastrophic failure of imagination. Yet their original intuition had been sound: at the point where they had been, progress had lain in the indeterminacy which old Ainsetain had refused to accept. And his refusal had been equally correct– in the long run. Only he had lacked the tools to prove it– the Saeba variables and the theories of infinite velocity and complex cause. His unified field existed, in Cetian physics, but it existed on terms which he might not have been willing to accept; for the velocity of light as a limiting factor had been essential to his great theories. Both his Theories of Relativity were as beautiful, as valid, and as useful as ever after these centuries, and yet both depended upon a hypothesis that could not be proved true and that could be and had been proved, in certain circumstances, false.
But was not a theory of which all the elements were provably true a simple tautology? In the region of the unprovable, or even the disprovable, lay the only chance for breaking out of the circle and going ahead.
In which case, did the unprovability of the hypothesis of real coexistence– the problem which Shevek had been pounding his head against desperately for these last three days. and indeed these last ten years– really matter?
He had been groping and grabbing after certainty, as if it were something he could possess. He had been demanding a security, a guarantee, which is not granted, and which, if granted, would become a prison. By simply assuming the validity of real coexistence he was left free to use the lovely geometries of relativity; and then it would be possible to go ahead. The next step was perfectly clear. The coexistence of succession could be handled by a Saeban transformation series; thus approached, successivity and presence offered no antithesis at all. The fundamental unity of the Sequency and Simultaneity points of view became plain; the concept of interval served to connect the static and the dynamic aspect of the universe. How could he have stared at reality for ten years and not seen it? There would be no trouble at all in going on. Indeed he had already gone on. He was there. He saw all that was to come in this first, seemingly casual glimpse of the method, given him by his understanding of a failure in the distant past. The wall was down. The vision was both clear and whole. What he saw was simple, simpler than anything else. It was simplicity: and contained in it all complexity, all promise. It was revelation. It was the way clear, the way home, the light.”
Related material—
Time Fold, Halloween 2005, and May and Zan.
See also The Devil and Wallace Stevens—
“In a letter to Harriet Monroe, written December 23, 1926, Stevens refers to the Sapphic fragment that invokes the genius of evening: ‘Evening star that bringest back all that lightsome Dawn hath scattered afar, thou bringest the sheep, thou bringest the goat, thou bringest the child home to the mother.’ Christmas, writes Stevens, ‘is like Sappho’s evening: it brings us all home to the fold’ (Letters of Wallace Stevens, 248).”
— “The Archangel of Evening,” Chapter 5 of Wallace Stevens: The Intensest Rendezvous, by Barbara M. Fisher, The University Press of Virginia, 1990