Stanley E. Payne and J. A. Thas in 1983* (previous post) —
“… a 4×4 grid together with
the affine lines on it is AG(2,4).”
Payne and Thas of course use their own definition
of affine lines on a grid.
Actually, a 4×4 grid together with the affine lines on it
is, viewed in a different way, not AG(2,4) but rather AG(4,2).
For AG(4,2) in the proper context, see
Affine Groups on Small Binary Spaces and
The Galois Tesseract.
* And 26 years later, in 2009.
Click image to enlarge.
The above 35 projective lines, within a 4×4 array —
The above 15 projective planes, within a 4×4 array (in white) —
* See Galois Tesseract in this journal.
Yesterday's post suggests a review of the following —
|
Andries Brouwer, preprint, 1982:
"The Witt designs, Golay codes and Mathieu groups" Pages 8-9: Substructures of S(5, 8, 24) An octad is a block of S(5, 8, 24). Theorem 5.1
Let B0 be a fixed octad. The 30 octads disjoint from B0
the design of the points and affine hyperplanes in AG(4, 2), Proof…. … (iv) We have AG(4, 2).
(Proof: invoke your favorite characterization of AG(4, 2) An explicit construction of the vector space is also easy….) |
Related material: Posts tagged Priority.
The three parts of the figure in today's earlier post "Defining Form"—
— share the same vector-space structure:
| 0 | c | d | c + d |
| a | a + c | a + d | a + c + d |
| b | b + c | b + d | b + c + d |
| a + b | a + b + c | a + b + d | a + b + c + d |
(This vector-space a b c d diagram is from Chapter 11 of
Sphere Packings, Lattices and Groups , by John Horton
Conway and N. J. A. Sloane, first published by Springer
in 1988.)
The fact that any 4×4 array embodies such a structure was implicit in
the diamond theorem (February 1979). Any 4×4 array, regarded as
a model of the finite geometry AG(4, 2), may be called a Galois tesseract.
(So called because of the Galois geometry involved, and because the
16 cells of a 4×4 array with opposite edges identified have the same
adjacency pattern as the 16 vertices of a tesseract (see, for instance,
Coxeter's 1950 "Self-Dual Configurations and Regular Graphs," figures
5 and 6).)
A 1982 discussion of a more abstract form of AG(4, 2):
Source:
The above 1982 remarks by Brouwer may or may not have influenced
the drawing of the above 1988 Conway-Sloane diagram.
A post of September 1, The Galois Tesseract, noted that the interplay
of algebraic and geometric properties within the 4×4 array that forms
two-thirds of the Curtis Miracle Octad Generator (MOG) may first have
been described by Cullinane (AMS abstract 79T-A37, Notices , Feb. 1979).
Here is some supporting material—
The passage from Carmichael above emphasizes the importance of
the 4×4 square within the MOG.
The passage from Conway and Sloane, in a book whose first edition
was published in 1988, makes explicit the structure of the MOG's
4×4 square as the affine 4-space over the 2-element Galois field.
The passage from Curtis (1974, published in 1976) describes 35 sets
of four "special tetrads" within the 4×4 square of the MOG. These
correspond to the 35 sets of four parallel 4-point affine planes within
the square. Curtis, however, in 1976 makes no mention of the affine
structure, characterizing his 140 "special tetrads" rather by the parity
of their intersections with the square's rows and columns.
The affine structure appears in the 1979 abstract mentioned above—
The "35 structures" of the abstract were listed, with an application to
Latin-square orthogonality, in a note from December 1978—
See also a 1987 article by R. T. Curtis—
Further elementary techniques using the miracle octad generator, by R. T. Curtis. Abstract:
“In this paper we describe various techniques, some of which are already used by devotees of the art, which relate certain maximal subgroups of the Mathieu group M24, as seen in the MOG, to matrix groups over finite fields. We hope to bring out the wealth of algebraic structure* underlying the device and to enable the reader to move freely between these matrices and permutations. Perhaps the MOG was mis-named as simply an ‘octad generator’; in this paper we intend to show that it is in reality a natural diagram of the binary Golay code.”
(Received July 20 1987)
– Proceedings of the Edinburgh Mathematical Society (Series 2) (1989), 32: 345-353
* For instance:
Update of Sept. 4— This post is now a page at finitegeometry.org.
From this journal at 1:51 AM ET Thursday, September 8, 2022 —
"The pleasure comes from the illusion" . . .
Exercise:
Compare and contrast the following structure with the three
"bricks" of the R. T. Curtis Miracle Octad Generator (MOG).
Note that the 4-row-2-column "brick" at left is quite
different from the other two bricks, which together
show chevron variations within a Galois tesseract —
.
Further Weil remarks . . .
A Slew of Prayers
"The pleasure comes from the illusion
and the far from clear meaning;
once the illusion is dissipated,
and knowledge obtained, one becomes
indifferent at the same time;
at least in the Gitâ there is a slew of prayers
(slokas) on the subject, each one more final
than the previous ones."
* —
From the previous post, "The Large Language Model,"
a passage from Wikipedia —
"… sometimes large models undergo a 'discontinuous phase shift'
where the model suddenly acquires substantial abilities not seen
in smaller models. These are known as 'emergent abilities,' and
have been the subject of substantial study." — Wikipedia
Compare and contrast
this with the change undergone by a "small space model,"
that of the finite affine 4-space A with 16 points (a Galois tesseract ),
when it is augmented by an eight-point "octad." The 30 eight-point
hyperplanes of A then have a natural extension within the new
24-point set to 759 eight-point octads, and the 322,560 affine
automorphisms of the space expand to the 244,823,040 Mathieu
automorphisms of the 759-octad set — a (5, 8, 24) Steiner system.
For a visual analogue of the enlarged 24-point space and some remarks
on analogy by Simone Weil's brother, a mathematician, see this journal
on September 8 and 9, 2022.
“You’re literally looking for like a one in a million thing.
You filter out the 999,999 of the boring ones, then
you’ve got something that’s weird, and then that’s worth
further exploration.”
— Quote from a mathematics story today at Gizmodo
A different "one in a million" mathematics story —
On Steiner Quadruple Systems of Order 16.
See also Galois Tesseract.
"A struggling music producer sells his soul to a 1970s drum machine."
— Summary of a short film by Kevin Ignatius, "Hook Man."
The music producer pawns his current drum device
and acquires a demonic 1970s machine.
Artistic symbolism —
The 16-pad device at left may be viewed by enthusiasts of ekphrasis
as a Galois tesseract, and the machine at right as the voice of
Hal Foster, an art theorist who graduated from Princeton in 1977.
For an example of Foster's prose style, see
the current London Review of Books.
André Weil in 1940 on analogy in mathematics —
| . "Once it is possible to translate any particular proof from one theory to another, then the analogy has ceased to be productive for this purpose; it would cease to be at all productive if at one point we had a meaningful and natural way of deriving both theories from a single one. In this sense, around 1820, mathematicians (Gauss, Abel, Galois, Jacobi) permitted themselves, with anguish and delight, to be guided by the analogy between the division of the circle (Gauss’s problem) and the division of elliptic functions. Today, we can easily show that both problems have a place in the theory of abelian equations; we have the theory (I am speaking of a purely algebraic theory, so it is not a matter of number theory in this case) of abelian extensions. Gone is the analogy: gone are the two theories, their conflicts and their delicious reciprocal reflections, their furtive caresses, their inexplicable quarrels; alas, all is just one theory, whose majestic beauty can no longer excite us. Nothing is more fecund than these slightly adulterous relationships; nothing gives greater pleasure to the connoisseur, whether he participates in it, or even if he is an historian contemplating it retrospectively, accompanied, nevertheless, by a touch of melancholy. The pleasure comes from the illusion and the far from clear meaning; once the illusion is dissipated, and knowledge obtained, one becomes indifferent at the same time; at least in the Gitâ there is a slew of prayers (slokas) on the subject, each one more final than the previous ones." |
"The pleasure comes from the illusion" . . .
Exercise:
Compare and contrast the following structure with the three
"bricks" of the R. T. Curtis Miracle Octad Generator (MOG).
Note that the 4-row-2-column "brick" at left is quite
different from the other two bricks, which together
show chevron variations within a Galois tesseract —
Note the three quadruplets of parallel edges in the 1984 figure above.
The above Gates article appeared earlier, in the June 2010 issue of
Physics World , with bigger illustrations. For instance —
Exercise: Describe, without seeing the rest of the article,
the rule used for connecting the balls above.
Wikipedia offers a much clearer picture of a (non-adinkra) tesseract —
And then, more simply, there is the Galois tesseract —
For parts of my own world in June 2010, see this journal for that month.
The above Galois tesseract appears there as follows:
See also the Klein correspondence in a paper from 1968
in yesterday's 2:54 PM ET post.
| Name Tag | .Space | .Group | .Art |
|---|---|---|---|
| Box4 |
2×2 square representing the four-point finite affine geometry AG(2,2). (Box4.space) |
S4 = AGL(2,2) (Box4.group) |
(Box4.art) |
| Box6 |
3×2 (3-row, 2-column) rectangular array representing the elements of an arbitrary 6-set. |
S6 | |
| Box8 | 2x2x2 cube or 4×2 (4-row, 2-column) array. | S8 or A8 or AGL(3,2) of order 1344, or GL(3,2) of order 168 | |
| Box9 | The 3×3 square. | AGL(2,3) or GL(2,3) | |
| Box12 | The 12 edges of a cube, or a 4×3 array for picturing the actions of the Mathieu group M12. | Symmetries of the cube or elements of the group M12 | |
| Box13 | The 13 symmetry axes of the cube. | Symmetries of the cube. | |
| Box15 |
The 15 points of PG(3,2), the projective geometry of 3 dimensions over the 2-element Galois field. |
Collineations of PG(3,2) | |
| Box16 |
The 16 points of AG(4,2), the affine geometry of 4 dimensions over the 2-element Galois field. |
AGL(4,2), the affine group of |
|
| Box20 | The configuration representing Desargues's theorem. | ||
| Box21 | The 21 points and 21 lines of PG(2,4). | ||
| Box24 | The 24 points of the Steiner system S(5, 8, 24). | ||
| Box25 | A 5×5 array representing PG(2,5). | ||
| Box27 |
The 3-dimensional Galois affine space over the 3-element Galois field GF(3). |
||
| Box28 | The 28 bitangents of a plane quartic curve. | ||
| Box32 |
Pair of 4×4 arrays representing orthogonal Latin squares. |
Used to represent elements of AGL(4,2) |
|
| Box35 |
A 5-row-by-7-column array representing the 35 lines in the finite projective space PG(3,2) |
PGL(3,2), order 20,160 | |
| Box36 | Eurler's 36-officer problem. | ||
| Box45 | The 45 Pascal points of the Pascal configuration. | ||
| Box48 | The 48 elements of the group AGL(2,3). | AGL(2,3). | |
| Box56 |
The 56 three-sets within an 8-set or |
||
| Box60 | The Klein configuration. | ||
| Box64 | Solomon's cube. |
— Steven H. Cullinane, March 26-27, 2022
The geometry of the 4×4 square may be associated with the name
Galois, as in "the Galois tesseract," or similarly with the name Kummer.
Here is a Google image search using the latter name —
(Click to enlarge.)
The time of the previous post was 4:46 AM ET today.
Fourteen minutes later —
"I'm a groupie, really." — Murray Bartlett in today's online NY Times
The previous post discussed group actions on a 3×3 square array. A tune
about related group actions on a 4×4 square array (a Galois tesseract ) . . .
From "Mathieu Moonshine and Symmetry Surfing" —
(Submitted on 29 Sep 2016, last revised 22 Jan 2018)
by Matthias R. Gaberdiel (1), Christoph A. Keller (2),
and Hynek Paul (1)
(1) Institute for Theoretical Physics, ETH Zurich
(2) Department of Mathematics, ETH Zurich
https://arxiv.org/abs/1609.09302v2 —
"This presentation of the symmetry groups Gi is
particularly well-adapted for the symmetry surfing
philosophy. In particular it is straightforward to
combine them into an overarching symmetry group G
by combining all the generators. The resulting group is
the so-called octad group
G = (Z2)4 ⋊ A8 .
It can be described as a maximal subgroup of M24
obtained by the setwise stabilizer of a particular
'reference octad' in the Golay code, which we take
to be O9 = {3,5,6,9,15,19,23,24} ∈ 𝒢24. The octad
subgroup is of order 322560, and its index in M24
is 759, which is precisely the number of
different reference octads one can choose."
This "octad group" is in fact the symmetry group of the affine 4-space over GF(2),
so described in 1979 in connection not with the Golay code but with the geometry
of the 4×4 square.* Its nature as an affine group acting on the Golay code was
known long before 1979, but its description as an affine group acting on
the 4×4 square may first have been published in connection with the
Cullinane diamond theorem and Abstract 79T-A37, "Symmetry invariance in a
diamond ring," by Steven H. Cullinane in Notices of the American Mathematical
Society , February 1979, pages A-193, 194.
* The Galois tesseract .
Update of March 15, 2020 —
Conway and Sloane on the "octad group" in 1993 —
The phrase "jewel box" in a New York Times obituary online this afternoon
suggests a review. See "And He Built a Crooked House" and Galois Tesseract.
The 4×4 square may also be called the Galois Tesseract .
By analogy, the 4x4x4 cube may be called the Galois Hexeract .
The previous post, "Tesserae for a Tesseract," contains the following
passage from a 1987 review of a book about Finnegans Wake —
"Basically, Mr. Bishop sees the text from above
and as a whole — less as a sequential story than
as a box of pied type or tesserae for a mosaic,
materials for a pattern to be made."
A set of 16 of the Wechsler cubes below are tesserae that
may be used to make patterns in the Galois tesseract.
Another Bellevue story —
“History, Stephen said, is a nightmare
from which I am trying to awake.”
— James Joyce, Ulysses
A Buddhist view —
“Just fancy a scale model of Being
made out of string and cardboard.”
— Nanavira Thera, 1 October 1957,
on a model of Kummer’s Quartic Surface
mentioned by Eddington
A Christian view —
A formal view —
From a Log24 search for High Concept:
See also Galois Tesseract.
The title was suggested by the name "ARTI" of an artificial
intelligence in the new film 2036: Origin Unknown.
The Eye of ARTI —
See also a post of May 19, "Uh-Oh" —
— and a post of June 6, "Geometry for Goyim" —
Mystery box merchandise from the 2011 J. J. Abrams film Super 8
An arty fact I prefer, suggested by the triangular computer-eye forms above —
This is from the July 29, 2012, post The Galois Tesseract.
See as well . . .
"By an archetype I mean a systematic repertoire
of ideas by means of which a given thinker describes,
by analogical extension , some domain to which
those ideas do not immediately and literally apply."
— Max Black in Models and Metaphors
(Cornell, 1962, p. 241)
"Others … spoke of 'ultimate frames of reference' …."
— Ibid.
A "frame of reference" for the concept four quartets —
A less reputable analogical extension of the same
frame of reference —
Madeleine L'Engle in A Swiftly Tilting Planet :
"… deep in concentration, bent over the model
they were building of a tesseract:
the square squared, and squared again…."
See also the phrase Galois tesseract .
"With respect to the story's content, the frame thus acts
both as an inclusion of the exterior and as an exclusion
of the interior: it is a perturbation of the outside at the
very core of the story's inside, and as such, it is a blurring
of the very difference between inside and outside."
— Shoshana Felman on a Henry James story, p. 123 in
"Turning the Screw of Interpretation,"
Yale French Studies No. 55/56 (1977), pp. 94-207.
Published by Yale University Press.
See also the previous post and The Galois Tesseract.
The “Black” of the title refers to the previous post.
For the “Well,” see Hexagram 48.
Related material —
The Galois Tesseract and, more generally, Binary Coordinate Systems.
Or: The Square
"What we do may be small, but it has
a certain character of permanence."
— G. H. Hardy
* See Expanding the Spielraum in this journal.
From a review of the 2016 film "Arrival" —
"A seemingly off-hand reference to Abbott and Costello
is our gateway. In a movie as generally humorless as Arrival,
the jokes mean something. Ironically, it is Donnelly, not Banks,
who initiates the joke, naming the verbally inexpressive
Heptapod aliens after the loquacious Classical Hollywood
comedians. The squid-like aliens communicate via those beautiful,
cryptic images. Those signs, when thoroughly comprehended,
open the perceiver to a nonlinear conception of time; this is
Sapir-Whorf taken to the ludicrous extreme."
— Jordan Brower in the Los Angeles Review of Books
Further on in the review —
"Banks doesn’t fully understand the alien language, but she
knows it well enough to get by. This realization emerges
most evidently when Banks enters the alien ship and, floating
alongside Costello, converses with it in their picture-language.
She asks where Abbott is, and it responds — as presented
in subtitling — that Abbott 'is death process.'
'Death process' — dying — is not idiomatic English, and what
we see, written for us, is not a perfect translation but a
rendering of Banks’s understanding. This, it seems to me, is a
crucial moment marking the hard limit of a human mind,
working within the confines of human language to understand
an ultimately intractable xenolinguistic system."
For what may seem like an intractable xenolinguistic system to
those whose experience of mathematics is limited to portrayals
by Hollywood, see the previous post —
van Lint and Wilson Meet the Galois Tesseract.
The death process of van Lint occurred on Sept. 28, 2004.
Pinterest boards uploaded to the new m759.net/piwigo —
Update of May 2 —
Update of May 3 —
Update of May 8 —
Art Space board created at Pinterest
From a Google image search yesterday —
Sources (left to right, top to bottom) —
Math Guy (July 16, 2014)
The Galois Tesseract (Sept. 1, 2011)
The Full Force of Roman Law (April 21, 2014)
A Great Moonshine (Sept. 25, 2015)
A Point of Identity (August 8, 2016)
Pascal via Curtis (April 6, 2013)
Correspondences (August 6, 2011)
Symmetric Generation (Sept. 21, 2011)
For geeks* —
" Domain, Domain on the Range , "
where Domain = the Galois tesseract and
Range = the four-element Galois field.
This post was suggested by the previous post,
by a Log24 search for Knight + Move, and by
the phrase "discouraging words" found in that search.
* A term from the 1947 film "Nightmare Alley."
The incidences of points and planes in the
Möbius 84 configuration (8 points and 8 planes,
with 4 points on each plane and 4 planes on each point),
were described by Coxeter in a 1950 paper.*
A table from Monday's post summarizes Coxeter's
remarks, which described the incidences in
spatial terms, with the points and planes as the vertices
and face-planes of two mutually inscribed tetrahedra —
Monday's post, "Gallucci's Möbius Configuration,"
may not be completely intelligible unless one notices
that Coxeter has drawn some of the intersections in his
Fig. 24, a schematic representation of the point-plane
incidences, as dotless, and some as hollow dots. The figure,
"Gallucci's version of Möbius's 84," is shown below.
The hollow dots, representing the 8 points (as opposed
to the 8 planes ) of the configuration, are highlighted in blue.
Here a plane (represented by a dotless intersection) contains
the four points that are represented in the square array as lying
in the same row or same column as the plane.
The above Möbius incidences appear also much earlier in
Coxeter's paper, in figures 6 and 5, where they are shown
as describing the structure of a hypercube.
In figures 6 and 5, the dotless intersections representing
planes have been replaced by solid dots. The hollow dots
have again been highlighted in blue.
Figures 6 and 5 demonstrate the fact that adjacency in the set of
16 vertices of a hypercube is isomorphic to adjacency in the set
of 16 subsquares of a square 4×4 array, provided that opposite
sides of the array are identified, as in Fig. 6. The digits in
Coxeter's labels above may be viewed as naming the positions
of the 1's in (0,1) vectors (x4, x3, x2, x1) over the two-element
Galois field.† In that context, the 4×4 array may be called, instead
of a Möbius hypercube , a Galois tesseract .
* "Self-Dual Configurations and Regular Graphs,"
Bulletin of the American Mathematical Society,
Vol. 56 (1950), pp. 413-455
† The subscripts' usual 1-2-3-4 order is reversed as a reminder
that such a vector may be viewed as labeling a binary number
from 0 through 15, or alternately as labeling a polynomial in
the 16-element Galois field GF(24). See the Log24 post
Vector Addition in a Finite Field (Jan. 5, 2013).
(Continued from July 16, 2014.)
Some background from Wikipedia:
"Friedrich Ernst Peter Hirzebruch ForMemRS[2]
(17 October 1927 – 27 May 2012)
was a German mathematician, working in the fields of topology,
complex manifolds and algebraic geometry, and a leading figure
in his generation. He has been described as 'the most important
mathematician in Germany of the postwar period.'
[3][4][5][6][7][8][9][10][11]"
A search for citations of the A. E. Brouwer paper in
the previous post yields a quotation from the preface
to the third ("2013") edition of Wolfgang Ebeling's
Lattices and Codes: A Course Partially Based
on Lectures by Friedrich Hirzebruch , a book
reportedly published on September 19, 2012 —
|
"Sadly, on May 27 this year, Friedrich Hirzebruch, Hannover, July 2012 Wolfgang Ebeling "
(Prof. Dr. Wolfgang Ebeling, Institute of Algebraic Geometry, |
Also sadly …
From H. S. M. Coxeter's 1950 paper
"Self-Dual Configurations and Regular Graphs,"
a 4×4 array and a more perspicuous rearrangement—
(Click image to enlarge.)
The above rearrangement brings Coxeter's remarks into accord
with the webpage The Galois Tesseract.
Update of Thursday, March 26, 2015 —
For an explanation of Coxeter's Fig. 24, see Thursday's later
post titled "The Möbius Hypercube."
Continued from June 17, 2013
(John Baez as a savior for atheists):
As an atheists-savior, I prefer Galois…
The geometry underlying a figure that John Baez
posted four days ago, "A Hypercube of Bits," is
Galois geometry —
See The Galois Tesseract and an earlier
figure from Log24 on May 21, 2007:
For the genesis of the figure,
see The Geometry of Logic.
From Zettel (repunctuated for clarity):
249. « Nichts leichter, als sich einen 4-dimensionalen Würfel
vorstellen! Er schaut so aus… »
"Nothing easier than to imagine a 4-dimensional cube!
It looks like this…
[Here the editor supplied a picture of a 4-dimensional cube
that was omitted by Wittgenstein in the original.]
« Aber das meine ich nicht, ich meine etwas wie…
"But I don't mean that, I mean something like…
…nur mit 4 Ausdehnungen! »
but with four dimensions!
« Aber das ist nicht, was ich dir gezeigt habe,
eben etwas wie…
"But isn't what I showed you like…
…nur mit 4 Ausdehnungen? »
…only with four dimensions?"
« Nein; das meine ich nicht! »
"No, I don't mean that!"
« Was aber meine ich? Was ist mein Bild?
Nun der 4-dimensionale Würfel, wie du ihn gezeichnet hast,
ist es nicht ! Ich habe jetzt als Bild nur die Worte und
die Ablehnung alles dessen, was du mir zeigen kanst. »
"But what do I mean? What is my picture?
Well, it is not the four-dimensional cube
as you drew it. I have now for a picture only
the words and my rejection of anything
you can show me."
"Here's your damn Bild , Ludwig —"
Context: The Galois Tesseract.
Introducing a group of 322,560 affine transformations of Dürer’s ‘Magic’ Square
The four vector-space substructures of digits in 1st, 2nd, 3rd, 4th place,
together with the diamond theorem, indicate that Dürer’s square “minus one”
can be transformed by permutations of rows, columns, and quadrants to a
square with (decimal) digits in the usual numerical order, increasing from
top left to bottom right. Such permutations form a group of order 322,560.
(Continued from Vector Addition in a Finite Field, Twelfth Night, 2013.)
The page of Whitehead linked to this morning
suggests a review of Polster's tetrahedral model
of the finite projective 3-space PG(3,2) over the
two-element Galois field GF(2).
|
The above passage from Whitehead's 1906 book suggests
that the tetrahedral model may be older than Polster thinks.
Shown at right below is a correspondence between Whitehead's
version of the tetrahedral model and my own square model,
based on the 4×4 array I call the Galois tesseract (at left below).
(Click to enlarge.)
"… this notion of ‘depth’ is an elusive one
even for a mathematician who can recognize it…."
— G. H. Hardy, A Mathematician's Apology
Part I: An Inch Deep
Part II: An Inch Wide
See a search for "square inch space" in this journal.
See also recent posts with the tag depth.
The sixteen-dot square array in yesterday’s noon post suggests
the following remarks.
“This is the relativity problem: to fix objectively a class of
equivalent coordinatizations and to ascertain the group of
transformations S mediating between them.”
— Hermann Weyl, The Classical Groups ,
Princeton University Press, 1946, p. 16
The Galois tesseract appeared in an early form in the journal
Computer Graphics and Art , Vol. 2, No. 1, February 1977—
The 1977 matrix Q is echoed in the following from 2002—
A different representation of Cullinane’s 1977 square model of the
16-point affine geometry over the two-element Galois field GF(2)
is supplied by Conway and Sloane in Sphere Packings, Lattices and Groups
(first published in 1988) :
Here a, b, c, d are basis vectors in the vector 4-space over GF(2).
(For a 1979 version of this vector space, see AMS Abstract 79T-A37.)
See also a 2011 publication of the Mathematical Association of America —
(On His Dies Natalis )…
This is asserted in an excerpt from…
"The smallest non-rank 3 strongly regular graphs
which satisfy the 4-vertex condition"
by Mikhail Klin, Mariusz Meszka, Sven Reichard, and Alex Rosa,
BAYREUTHER MATHEMATISCHE SCHRIFTEN 73 (2005), 152-212—
(Click for clearer image)
Note that Theorem 46 of Klin et al. describes the role
of the Galois tesseract in the Miracle Octad Generator
of R. T. Curtis (original 1976 version). The tesseract
(a 4×4 array) supplies the geometric part of the above
exceptional geometric-combinatorial isomorphism.
"How about another hand for the band?
They work real hard for it.
The Cherokee Cowboys, ladies and gentlemen."
— Ray Price, video, "Danny Boy Mid 80's Live"
Other deathly hallows suggested by today's NY Times—
Click the above image for posts from December 14.
That image mentions a death on August 5, 2005, in
"entertainment Mecca" Branson, Missouri.
Another note from August 5, 2005, reposted here
on Monday—
Happy birthday, Keith Richards.
Happy Beethoven's Birthday.
Related material: Abel 2005 and, more generally, Abel.
See also Visible Mathematics.
Odin's Jewel
Jim Holt, the author of remarks in yesterday's
Saturday evening post—
"It turns out that the Kyoto school of Buddhism
makes Heidegger seem like Rush Limbaugh—
it’s so rarified, I’ve never been able to
understand it at all. I’ve been knocking my head
against it for years."
— Vanity Fair Daily , July 16, 2012
Backstory: Odin + Jewel in this journal.
See also Odin on the Kyoto school —
For another version of Odin's jewel, see Log24
on the date— July 16, 2012— that Holt's Vanity Fair
remarks were published. Scroll to the bottom of the
"Mapping Problem continued" post for an instance of
the Galois tesseract —
The Kummer 166 configuration is the configuration of sixteen
6-sets within a 4×4 square array of points in which each 6-set
is determined by one of the 16 points of the array and
consists of the 3 other points in that point's row and the
3 other points in that point's column.
See Configurations and Squares.
The Wikipedia article Kummer surface uses a rather poetic
phrase* to describe the relationship of the 166 to a number
of other mathematical concepts — "geometric incarnation."
Related material from finitegeometry.org —
* Apparently from David Lehavi on March 18, 2007, at Citizendium .
The Galois tesseract appeared in an early form in the journal
Computer Graphics and Art , Vol. 2, No. 1, February 1977—
The Galois tesseract is the basis for a representation of the smallest
projective 3-space, PG(3,2), that differs from the representation at
Wolfram Demonstrations Project. For the latter, see yesterday’s post.
The tesseract representation underlies the diamond theorem, illustrated
below in its earliest form, also from the above February 1977 article—
As noted in a more recent version, the group described by
the diamond theorem is also the group of the 35 square
patterns within the 1976 Miracle Octad Generator (MOG) of
R. T. Curtis.
The Daily Princetonian today:
A different cover act, discussed here Saturday:
See also, in this journal, the Galois tesseract and the Crosswicks Curse.
"There is such a thing as a tesseract." — Crosswicks saying
The hypercube model of the 4-space over the 2-element Galois field GF(2):
The phrase Galois tesseract may be used to denote a different model
of the above 4-space: the 4×4 square.
MacWilliams and Sloane discussed the Miracle Octad Generator
(MOG) of R. T. Curtis further on in their book (see below), but did not
seem to realize in 1977 that the 4×4 structures within the MOG are
based on the Galois-tesseract model of the 4-space over GF(2).
The thirty-five 4×4 structures within the MOG:
Curtis himself first described these 35 square MOG patterns
combinatorially, (as his title indicated) rather than
algebraically or geometrically:
A later book co-authored by Sloane, first published in 1988,
did recognize the 4×4 MOG patterns as based on the 4×4
Galois-tesseract model.
Between the 1977 and 1988 Sloane books came the diamond theorem.
Update of May 29, 2013:
The Galois tesseract appeared in an early form in the journal
Computer Graphics and Art , Vol. 2, No. 1, February 1977
(the year the above MacWilliams-Sloane book was first published):
Best vs. Bester
The previous post ended with a reference mentioning Rosenhain.
For a recent application of Rosenhain's work, see
Desargues via Rosenhain (April 1, 2013).
From the next day, April 2, 2013:
"The proof of Desargues' theorem of projective geometry
comes as close as a proof can to the Zen ideal.
It can be summarized in two words: 'I see!' "
– Gian-Carlo Rota in Indiscrete Thoughts (1997)
Also in that book, originally from a review in Advances in Mathematics ,
Vol. 84, Number 1, Nov. 1990, p. 136:
See, too, in the Conway-Sloane book, the Galois tesseract …
and, in this journal, Geometry for Jews and The Deceivers , by Bester.
From an arXiv preprint submitted July 18, 2011,
and last revised on March 11, 2013 (version 4):
"By our construction, this vector space is the dual
of our hypercube F24 built on I \ O9. The vector space
structure of the latter, to our knowledge, is first
mentioned by Curtis in [Cur89]. Hence altogether
our proposition 2.3.4 gives a novel geometric
meaning in terms of Kummer geometry to the known
vector space structure on I \ O9."
[Cur89] reference:
R. T. Curtis, "Further elementary techniques using
the miracle octad generator," Proc. Edinburgh
Math. Soc. 32 (1989), 345-353 (received on
July 20, 1987).
— Anne Taormina and Katrin Wendland,
"The overarching finite symmetry group of Kummer
surfaces in the Mathieu group M 24 ,"
arXiv.org > hep-th > arXiv:1107.3834
"First mentioned by Curtis…."
No. I claim that to the best of my knowledge, the
vector space structure was first mentioned by me,
Steven H. Cullinane, in an AMS abstract submitted
in October 1978, some nine years before the
Curtis article.
|
Update of the above paragraph on July 6, 2013—
No. The vector space structure was described by
The vector space structure as it occurs in a 4×4 array |
See Notes on Finite Geometry for some background.
See in particular The Galois Tesseract.
For the relationship of the 1978 abstract to Kummer
geometry, see Rosenhain and Göpel Tetrads in PG(3,2).
"The proof of Desargues' theorem of projective geometry
comes as close as a proof can to the Zen ideal.
It can be summarized in two words: 'I see!' "
— Gian-Carlo Rota in Indiscrete Thoughts (1997)
Also in that book, originally from a review in Advances in Mathematics,
Vol. 84, Number 1, Nov. 1990, p. 136:
Related material:
Pascal and the Galois nocciolo ,
Conway and the Galois tesseract,
Gardner and Galois.
See also Rota and Psychoshop.
Today's previous post recalled a post
from ten years before yesterday's date.
The subject of that post was the
Galois tesseract.
Here is a post from ten years before
today's date.
The subject of that post is the Halmos
tombstone:
"The symbol 
is used throughout the entire book
in place of such phrases as 'Q.E.D.' or 'This
completes the proof of the theorem' to signal
the end of a proof."
— Measure Theory (1950)
For exact proportions, click on the tombstone.
For some classic mathematics related
to the proportions, see September 2003.
Story, Structure, and the Galois Tesseract
Recent Log24 posts have referred to the
"Penrose diamond" and Minkowski space.
The Penrose diamond has nothing whatever
to do with my 1976 monograph "Diamond Theory,"
except for the diamond shape and the connection
of the Penrose diamond to the Klein quadric—
The Klein quadric occurs in the five-dimensional projective space
over a field. If the field is the two-element Galois field GF(2), the
quadric helps explain certain remarkable symmetry properties
of the R. T. Curtis Miracle Octad Generator (MOG), hence of
the large Mathieu group M24. These properties are also
relevant to the 1976 "Diamond Theory" monograph.
For some background on the quadric, see (for instance)…
See also The Klein Correspondence,
Penrose Space-Time, and a Finite Model.
Related material:
|
"… one might crudely distinguish between philosophical – J. M. E. Hyland. "Proof Theory in the Abstract." (pdf) |
Those who prefer story to structure may consult
The finite (i.e., Galois) field GF(16),
according to J. J. Seidel in 1974—
The same field according to Steven H. Cullinane in 1986,
in its guise as the affine 4-space over GF(2)—
The same field, again disguised as an affine 4-space,
according to John H. Conway and N.J.A. Sloane in
Sphere Packings, Lattices, and Groups , first published in 1988—
The above figure by Conway and Sloane summarizes, using
a 4×4 array, the additive vector-space structure of the finite
field GF(16).
This structure embodies what in Euclidean space is called
the parallelogram rule for vector addition—
(Thanks to June Lester for the 3D (uvw) part of the above figure.)
For the transition from this colored Euclidean hypercube
(used above to illustrate the parallelogram rule) to the
4×4 Galois space (illustrated by Cullinane in 1979 and
Conway and Sloane in 1988— or later… I do not have
their book’s first edition), see Diamond Theory in 1937,
Vertex Adjacency in a Tesseract and in a 4×4 Array,
Spaces as Hypercubes, and The Galois Tesseract.
For some related narrative, see tesseract in this journal.
(This post has been added to finitegeometry.org.)
Update of August 9, 2013—
Coordinates for hypercube vertices derived from the
parallelogram rule in four dimensions were better
illustrated by Jürgen Köller in a web page archived in 2002.
Update of August 13, 2013—
The four basis vectors in the 2002 Köller hypercube figure
are also visible at the bottom of the hypercube figure on
page 7 of “Diamond Theory,” excerpts from a 1976 preprint
in Computer Graphics and Art , Vol. 2, No. 1, February 1977.
A predecessor: Coxeter’s 1950 hypercube figure from
“Self-Dual Configurations and Regular Graphs.”
Euclidean square and triangle—
Galois square and triangle—
Background—
This journal on the date of Hilton Kramer's death,
The Galois Tesseract, and The Purloined Diamond.
Background— George Steiner in this journal
and elsewhere—
"An intensity of outward attention —
interest, curiosity, healthy obsession —
was Steiner’s version of God’s grace."
— Lee Siegel in The New York Times ,
March 12, 2009
(See also Aesthetics of Matter in this journal on that date.)
Steiner in 1969 defined man as "a language animal."
Here is Steiner in 1974 on another definition—
Related material—
Also related — Kantor in 1981 on "exquisite finite geometries," and The Galois Tesseract.
"Debates about canonicity have been raging in my field
(literary studies) for as long as the field has been
around. Who's in? Who's out? How do we decide?"
— Stephen Ramsay, "The Hermeneutics of Screwing Around"
An example of canonicity in geometry—
"There are eight heptads of 7 mutually azygetic screws, each consisting of the screws having a fixed subscript (from 0 to 7) in common. The transformations of LF(4,2) correspond in a one-to-one manner with the even permutations on these heptads, and this establishes the isomorphism of LF(4,2) and A8. The 35 lines in S3 correspond uniquely to the separations of the eight heptads into two complementary sets of 4…."
— J.S. Frame, 1955 review of a 1954 paper by W.L. Edge,
"The Geometry of the Linear Fractional Group LF(4,2)"
Thanks for the Ramsay link are due to Stanley Fish
(last evening's online New York Times ).
For further details, see The Galois Tesseract.
J. H. Conway in 1971 discussed the role of an elementary abelian group
of order 16 in the Mathieu group M24. His approach at that time was
purely algebraic, not geometric—
For earlier (and later) discussions of the geometry (not the algebra )
of that order-16 group (i.e., the group of translations of the affine space
of 4 dimensions over the 2-element field), see The Galois Tesseract.
"Design is how it works." — Steve Jobs
From a commercial test-prep firm in New York City—
From the date of the above uploading—
|
|
From a New Year's Day, 2012, weblog post in New Zealand—
From Arthur C. Clarke, an early version of his 2001 monolith—
"So they left a sentinel, one of millions they have scattered
throughout the Universe, watching over all worlds with the
promise of life. It was a beacon that down the ages has been
patiently signaling the fact that no one had discovered it.
Perhaps you understand now why that crystal pyramid was set…."
The numerical (not crystal) pyramid above is related to a sort of
mathematical block design known as a Steiner system.
For its relationship to the graphic block design shown above,
see the webpages Block Designs and The Diamond Theorem
as well as The Galois Tesseract and R. T. Curtis's classic paper
"A New Combinatorial Approach to M24," which contains the following
version of the above numerical pyramid—
For graphic block designs, I prefer the blocks (and the parents)
of Grand Rapids to those of New York City.
For the barbed tail of Clarke's "Angel" story, see the New Zealand post
of New Year's Day mentioned above.
Mathematics —
(Some background for the Galois tesseract )
Narrative —
An essay on science and philosophy in the January 2012
Notices of the American Mathematical Society .
Note particularly the narrative explanation of the double-slit experiment—
"The assertion that elementary particles have
free will and follow Quality very closely leads to
some startling consequences. For instance, the
wave-particle duality paradox, in particular the baffling
results of the famous double slit experiment,
may now be reconsidered. In that experiment, first
conducted by Thomas Young at the beginning
of the nineteenth century, a point light source
illuminated a thin plate with two adjacent parallel
slits in it. The light passing through the slits
was projected on a screen behind the plate, and a
pattern of bright and dark bands on the screen was
observed. It was precisely the interference pattern
caused by the diffraction patterns of waves passing
through adjacent holes in an obstruction. However,
when the same experiment was carried out much
later, only this time with photons being shot at
the screen one at a time—the same interference
pattern resulted! But the Metaphysics of Quality
can offer an explanation: the photons each follow
Quality in their actions, and so either individually
or en masse (i.e., from a light source) will do the
same thing, that is, create the same interference
pattern on the screen."
This is from "a Ph.D. candidate in mathematics at the University of Calgary."
His essay is titled "A Perspective on Wigner’s 'Unreasonable Effectiveness
of Mathematics.'" It might better be titled "Ineffective Metaphysics."
Mathematics and Narrative, continued
"… a vision invisible, even ineffable, as ineffable as the Angels and the Universal Souls"
— Tom Wolfe, The Painted Word , 1975, quoted here on October 30th
"… our laughable abstractions, our wryly ironic po-mo angels dancing on the heads of so many mis-imagined quantum pins."
— Dan Conover on September 1st, 2011
"Recently I happened to be talking to a prominent California geologist, and she told me: 'When I first went into geology, we all thought that in science you create a solid layer of findings, through experiment and careful investigation, and then you add a second layer, like a second layer of bricks, all very carefully, and so on. Occasionally some adventurous scientist stacks the bricks up in towers, and these towers turn out to be insubstantial and they get torn down, and you proceed again with the careful layers. But we now realize that the very first layers aren't even resting on solid ground. They are balanced on bubbles, on concepts that are full of air, and those bubbles are being burst today, one after the other.'
I suddenly had a picture of the entire astonishing edifice collapsing and modern man plunging headlong back into the primordial ooze. He's floundering, sloshing about, gulping for air, frantically treading ooze, when he feels something huge and smooth swim beneath him and boost him up, like some almighty dolphin. He can't see it, but he's much impressed. He names it God."
— Tom Wolfe, "Sorry, but Your Soul Just Died," Forbes , 1996
"… Ockham's idea implies that we probably have the ability to do something now such that if we were to do it, then the past would have been different…"
— Stanford Encyclopedia of Philosophy
"Today is February 28, 2008, and we are privileged to begin a conversation with Mr. Tom Wolfe."
— Interviewer for the National Association of Scholars
From that conversation—
Wolfe : "People in academia should start insisting on objective scholarship, insisting on it, relentlessly, driving the point home, ramming it down the gullets of the politically correct, making noise! naming names! citing egregious examples! showing contempt to the brink of brutality!"
As for "mis-imagined quantum pins"…
This journal on the date of the above interview— February 28, 2008—
Illustration from a Perimeter Institute talk given on July 20, 2005
The date of Conover's "quantum pins" remark above (together with Ockham's remark above and the above image) suggests a story by Conover, "The Last Epiphany," and four posts from September 1st, 2011—
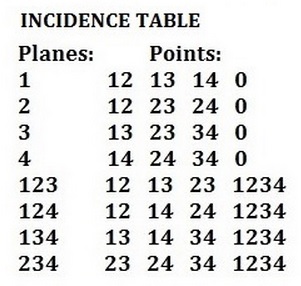
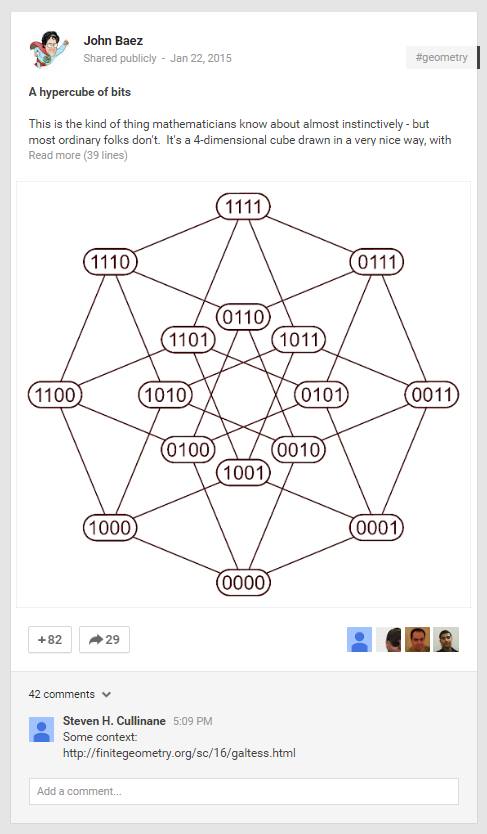
Boundary, How It Works, For Thor's Day, and The Galois Tesseract.
Those four posts may be viewed as either an exploration or a parody of the boundary between mathematics and narrative.
"There is such a thing as a tesseract." —A Wrinkle in Time
Today is day 256 of 2011, Programmers' Day.
Yesterday, Monday, R. W. Barraclough's website pictured the Octad of the Week—
" X never, ever, marks the spot."
See also The Galois Tesseract.
Paul Robeson in
"King Solomon's Mines," 1937—
The image above is an illustration from
"Romancing the Hyperspace," May 4, 2010.
This illustration, along with Georgia Brown's
song from "Cabin in the Sky"—
"There's honey in the honeycomb"—
suggests the following picture.
"What might have been and what has been
Point to one end, which is always present."
— Four Quartets
Powered by WordPress
.jpg){kind=link}
