Related quotations —
"So we beat on, boats against the current…." — F. Scott Fitzgerald
"There grows a tree in Paradise…." — Joan Baez
Related narrative — River of Death.
Related quotations —
"So we beat on, boats against the current…." — F. Scott Fitzgerald
"There grows a tree in Paradise…." — Joan Baez
Related narrative — River of Death.
From the above Baez essay —
"And when the hero arrives, there should be
a little flourish of trumpets, like:
And now we come to a key player:
the group of deck transformations."
This remark and Baez's statement that
"Ideally the tricks I’m suggesting here
will be almost invisible…."
suggest a non-mathematical "deck transformation"
that some will prefer —
In the March 21 Netflix series "3 Body Problem,"
the deck of the ship Judgment Day is transformed
in a spectacular manner by an invisible trick.



The above solar art is . . .
(By John Baez, cousin of Joan)
(The Baez art was also displayed here on Saturday, March 23, 2024 —
the second day of the 2024 Biennale in the Desert Sun article.)
Remarks by John Baez today suggest a flashback…
See John Baez this morning on Galois. Note that Baez's
report of Galois's dies natalis is in error.
The above title. by one Lee E. Mosley, is from
"CreateSpace Independent Publishing Platform;
1st edition (June 4, 2017)."
From the preface —
"So simple . . . ."
"Building blocks"? — See the literature of pop physics.
Natural companions to building blocks, are, of course,
"permutation groups."
See the oeuvre of physics writer John Baez —
For instance, in a Log24 post from the above Mosley
publication date — June 4, 2017 —
Mank, Baez, Collins — A trip back to Christmas Eve, 2021.
Related art (via Baez) for Josefine Lyche —

See also Lyche in Log24 posts tagged Star Cube.
The above cubic equation may also be written as
x3 – x – 1 = 0.
The equation occurred in my own work in 1985:
An architects' equation that appears also in Galois geometry.
For further details on the plastic number, see an article by
Siobhan Roberts on John Baez in The New York Times —
"… Évariste was born on October 25, 1811."
— Eric Temple Bell, Men of Mathematics
Related material —
But seriously . . .


(A sequel to the previous post — "To the Lighthouse")
From that same date . . .
|
Log24 on August 5, 2002 — "To really know a subject you've got to learn a bit of its history." — John Baez, August 4, 2002
"We both know what memories can bring; — Joan Baez, April 1975 "Venn considered three discs R, S, and T as typical subsets of a set U. The intersections of these discs and their complements divide U into 8 nonoverlapping regions." — History of Mathematics at St. Andrews "Who would not be rapt by the thought of such marvels?" — Saint Bonaventure on the Trinity |
"Who would not be rapt?" . . . Cristin Milioti? —

See as well Oct. 12, 2018 (and, more generally, Volvo) in this journal.
Related material:
It is not clear whether the above acronym
should be pronounced "psycho" or "sicko."
| Name Tag | .Space | .Group | .Art |
|---|---|---|---|
| Box4 |
2×2 square representing the four-point finite affine geometry AG(2,2). (Box4.space) |
S4 = AGL(2,2) (Box4.group) |
(Box4.art) |
| Box6 |
3×2 (3-row, 2-column) rectangular array representing the elements of an arbitrary 6-set. |
S6 | |
| Box8 | 2x2x2 cube or 4×2 (4-row, 2-column) array. | S8 or A8 or AGL(3,2) of order 1344, or GL(3,2) of order 168 | |
| Box9 | The 3×3 square. | AGL(2,3) or GL(2,3) | |
| Box12 | The 12 edges of a cube, or a 4×3 array for picturing the actions of the Mathieu group M12. | Symmetries of the cube or elements of the group M12 | |
| Box13 | The 13 symmetry axes of the cube. | Symmetries of the cube. | |
| Box15 |
The 15 points of PG(3,2), the projective geometry of 3 dimensions over the 2-element Galois field. |
Collineations of PG(3,2) | |
| Box16 |
The 16 points of AG(4,2), the affine geometry of 4 dimensions over the 2-element Galois field. |
AGL(4,2), the affine group of |
|
| Box20 | The configuration representing Desargues's theorem. | ||
| Box21 | The 21 points and 21 lines of PG(2,4). | ||
| Box24 | The 24 points of the Steiner system S(5, 8, 24). | ||
| Box25 | A 5×5 array representing PG(2,5). | ||
| Box27 |
The 3-dimensional Galois affine space over the 3-element Galois field GF(3). |
||
| Box28 | The 28 bitangents of a plane quartic curve. | ||
| Box32 |
Pair of 4×4 arrays representing orthogonal Latin squares. |
Used to represent elements of AGL(4,2) |
|
| Box35 |
A 5-row-by-7-column array representing the 35 lines in the finite projective space PG(3,2) |
PGL(3,2), order 20,160 | |
| Box36 | Eurler's 36-officer problem. | ||
| Box45 | The 45 Pascal points of the Pascal configuration. | ||
| Box48 | The 48 elements of the group AGL(2,3). | AGL(2,3). | |
| Box56 |
The 56 three-sets within an 8-set or |
||
| Box60 | The Klein configuration. | ||
| Box64 | Solomon's cube. |
— Steven H. Cullinane, March 26-27, 2022
The title refers to a man called by John Baez
“The infamous pseudohistorian Eric Temple Bell.”
(See my post The Magpie.)
Today the American Mathematical Society (AMS) has
an obituary for Donald Babbitt (1936-2020), who
reportedly died on October 10.
Babbitt is the co-author of an article on Bell from the
June/July 2013 AMS Notices .
Jung's phrase "'four-square' Heavenly City" in the previous post
suggests a geometric object… the 4×4 square —
The "twelve gates" at the sides of the above figure suggest a song —
The Baez date above suggests in turn a review of
the Jan. 4, 2014, post "Heaven's Gate,"
on the death of film producer Saul Zaentz.
Related material —
The "Heavenly City" is perhaps not Cambridge, Massachusetts.
Recall as well Jean Simmons preaching the Foursquare Gospel
in the 1960 film classic "Elmer Gantry" —
For the Toro , see Pierre Cartier in 2001 on the barber of Seville and
“The evolution of concepts of space and symmetry.”
For the Torino , see . . .
“… the ultimate goal of the present essay
which is to illustrate the historic
evolution of the concepts of Space and Symmetry “
— Pp. 157-158 of the above book.
See also Fré et al. , “The role of PSL(2,7) in M-theory”
(2018-2019) at http://arxiv.org/abs/1812.11049v2 ,
esp. Section 4, “Theory of the simple group PSL(2,7)”
on pages 11-27, and remarks on PSL(2,7) in this journal.
Related material —
Cube Bricks 1984 —
From "Tomorrowland" (2015) —

From John Baez (2018) —
See also this morning's post Perception of Space
and yesterday's Exploring Schoolgirl Space.
The three previous posts have now been tagged . . .
Tetrahedron vs. Square and Triangle vs. Cube.
Related material —
Tetrahedron vs. Square:
Labeling the Tetrahedral Model (Click to enlarge) —
Triangle vs. Cube:

… and, from the date of the above John Baez remark —
A remark on coordinatization linked to by John Baez today —
This suggests a more historical perspective:
See as well a search for Interpenetration in this journal.
The Crosswicks Curse Continues . . .
"There is such a thing as geometry."
— Saying adapted from a 1962 young-adult novel.
This journal on the above date, October 17, 2008 —
“Every musician wants to do something of lasting quality,
something which will hold up for a long time, and
I guess we did it with ‘Stairway.'”
— Jimmy Page on “Stairway to Heaven“
Scholium —
"Kummer " in German means "sorrow."
Related material —
Other posts now tagged Dolmen.
The title is from a phrase spoken, notably, by Yul Brynner
to Christopher Plummer in the 1966 film “Triple Cross.”
Related structures —
Greg Egan’s animated image of the Klein quartic —
For a smaller tetrahedral arrangement, within the Steiner quadruple
system of order 8 modeled by the eightfold cube, see a book chapter
by Michael Huber of Tübingen —

For further details, see the June 29 post Triangles in the Eightfold Cube.
See also, from an April 2013 philosophical conference:
| Abstract for a talk at the City University of New York:
The Experience of Meaning Once the question of truth is settled, and often prior to it, what we value in a mathematical proof or conjecture is what we value in a work of lyric art: potency of meaning. An absence of clutter is a feature of such artifacts: they possess a resonant clarity that allows their meaning to break on our inner eye like light. But this absence of clutter is not tantamount to ‘being simple’: consider Eliot’s Four Quartets or Mozart’s late symphonies. Some truths are complex, and they are simplified at the cost of distortion, at the cost of ceasing to be truths. Nonetheless, it’s often possible to express a complex truth in a way that precipitates a powerful experience of meaning. It is that experience we seek — not simplicity per se , but the flash of insight, the sense we’ve seen into the heart of things. I’ll first try to say something about what is involved in such recognitions; and then something about why an absence of clutter matters to them. |
For the talk itself, see a YouTube video.
The conference talks also appear in a book.
The book begins with an epigraph by Hilbert —

From a post of July 25, 2008, “56 Triangles,” on the Klein quartic
and the eightfold cube —
“Baez’s discussion says that the Klein quartic’s 56 triangles
can be partitioned into 7 eight-triangle Egan ‘cubes’ that
correspond to the 7 points of the Fano plane in such a way
that automorphisms of the Klein quartic correspond to
automorphisms of the Fano plane. Show that the
56 triangles within the eightfold cube can also be partitioned
into 7 eight-triangle sets that correspond to the 7 points of the
Fano plane in such a way that (affine) transformations of the
eightfold cube induce (projective) automorphisms of the Fano plane.”
Related material from 1975 —
More recently …
The most recent post in the "Visual Insight" blog of the
American Mathematical Society was by John Baez on Jan. 1, 2017 —
A visually related concept — See Solomon's Cube in this journal.
Chronologically related — Posts now tagged New Year's Day 2017.
Solomon's cube is the 4x4x4 case of the diamond theorem —
From this journal on August 18, 2015, "A Wrinkle in Terms" —
For two misuses by John Baez of the phrase “permutation group”
at the n-Category Café, see “A Wrinkle in the Mathematical Universe”
and “Re: A Wrinkle…” —
“There is such a thing as a permutation group.”
— Adapted from A Wrinkle in Time , by Madeleine L’Engle
* See RIP, Time Cube at gizmodo.com (September 1, 2015).

Related material —
See the story of a British man who reportedly had a doctorate in
physics and mathematics and became a witchcraft enthusiast.
He is said to have died at 85 on September 11, 2016.
As Wittgenstein noted, it is not always clear whether the pentagram
expresses a mathematical or an experiential proposition.
For some mathematical propositions related to the pentagram,
see (for instance) John Baez's slides for his 2008 Glasgow
lecture on the number 5.
For som experiential propositions, see Pentagram in this journal.
Or, "An Education Continued"
This journal on May 29, 2010, had a followup to
the previous day's post "Multispeech for Oxford"—
An Oxford workshop, "Quantum Physics and Logic," began
on the date of the above Log24 "Packed" post, May 29, 2010.
The first talk was by John Baez —

Baez's notes on his talk begin …
"Duality has many manifestations in logic and physics." —
Yes, it does.
"Dust is a fictional elementary particle that is of
fundamental importance within the story."
— Wikipedia on Philip Pullman's His Dark Materials trilogy
A review of posts tagged Kabbalah yields —
|
"If all that 'matters' are fundamentally mathematical relationships, then there ceases to be any important difference between the actual and the possible. (Even if you aren't a mathematical Platonist, you can always find some collection of particles of dust to fit any required pattern. In Permutation City this is called the 'logic of the dust' theory.)….
— Danny Yee, review of Permutation City , |
See also in this journal a search for Dark Matter.
This morning at 11:44 I happened upon …
This was published as …
Toshiyuki Katsura, Shigeyuki Kondo, Ichiro Shimada,
"On the supersingular K3 surface in characteristic 5 with Artin invariant 1,"
Michigan Mathematical Journal , vol. 63, issue 4 (Dec. 2014), 803–844.
Related material from later today —
See also earlier Log24 remarks on the Hoffman-Singleton graph
and a remark on geometry for Princeton.
"Once upon a midnight dreary, while I pondered, weak and weary,
Over many a quaint and curious volume of forgotten lore…."
— Edgar Allan Poe, 1845 (link added)
"The infamous pseudohistorian Eric Temple Bell
begins his book 'The Magic of Numbers' as follows:
The hero of our story is Pythagoras…."
Related material —
See also "Temple Bell" in this journal.
From a post of July 24, 2011 —

A review —
“The story, involving the Knights Templar, the Vatican, sunken treasure,
the fate of Christianity and a decoding device that looks as if it came out of
a really big box of medieval Cracker Jack, is the latest attempt to combine
Indiana Jones derring-do with ‘Da Vinci Code’ mysticism.”
A feeble attempt at a purely mathematical "decoding device"
from this journal earlier this month —

For some background, see a question by John Baez at Math Overflow
on Aug. 20, 2015.
The nonexistence of a 24-cycle in the large Mathieu group
might discourage anyone hoping for deep new insights from
the above figure.
See Marston Conder's "Symmetric Genus of the Mathieu Groups" —

Click to enlarge:
For the hypercube as a vector space over the two-element field GF(2),
see a search in this journal for Hypercube + Vector + Space .
For connections with the related symplectic geometry, see Symplectic
in this journal and Notes on Groups and Geometry, 1978-1986.
For the above 1976 hypercube (or tesseract ), see "Diamond Theory,"
by Steven H. Cullinane, Computer Graphics and Art , Vol. 2, No. 1,
Feb. 1977, pp. 5-7.
The latest Visual Insight post at the American Mathematical
Society website discusses group actions on the McGee graph,
pictured as 24 points arranged in a circle that are connected
by 36 symmetrically arranged edges.
Wikipedia remarks that …
"The automorphism group of the McGee graph
is of order 32 and doesn't act transitively upon
its vertices: there are two vertex orbits of lengths
8 and 16."
The partition into 8 and 16 points suggests, for those familiar
with the Miracle Octad Generator and the Mathieu group M24,
the following exercise:
Arrange the 24 points of the projective line
over GF(23) in a circle in the natural cyclic order
( ∞, 1, 2, 3, … , 22, 0 ). Can the McGee graph be
modeled by constructing edges in any natural way?

In other words, if the above set of edges has no
"natural" connection with the 24 points of the
projective line over GF(23), does some other
set of edges in an isomorphic McGee graph
have such a connection?
Update of 9:20 PM ET Sept. 20, 2015:
Backstory: A related question by John Baez
at Math Overflow on August 20.
Related material:
From the website of the American Mathematical Society today,
a column by John Baez that was falsely backdated to Sept. 1, 2015 —
Compare and contrast this Baez column
with the posts in the above
Log24 search for "Symplectic."
Updates after 9 PM ET Sept. 17, 2015 —
Related wrinkles in time:
Baez's preceding Visual Insight post, titled
"Tutte-Coxeter Graph," was dated Aug. 15, 2015.
This seems to contradict the AMS home page headline
of Sept. 5, 2015, that linked to Baez's still earlier post
"Heawood Graph," dated Aug. 1. Also, note the
reference in "Tutte-Coxeter Graph" to Baez's related
essay — dated August 17, 2015 —
The phrase “the permutation group Sn” refers to a
particular group of permutations that act on an
n -element set N— namely, all of them. For a given n ,
there are, in general, many permutation groups that
act on N. All but one are smaller than Sn .
In other words, the phrase “the permutation group Sn”
does not imply that “Sn ” is a symbol for a structure
associated with n called “the permutation group.”
It is instead a symbol for “the symmetric group,” the largest
of (in general) many permutation groups that act on N.
This point seems to have escaped John Baez.
For two misuses by Baez of the phrase “permutation group” at the
n-Category Café, see “A Wrinkle in the Mathematical Universe”
and “Re: A Wrinkle…” —


“There is such a thing as a permutation group.”
— Adapted from A Wrinkle in Time , by Madeleine L’Engle
Backstory: Other posts tagged “Cryptomorphisms,”
and the word itself in Wikipedia.
Compare and contrast:
Continued from June 17, 2013
(John Baez as a savior for atheists):
As an atheists-savior, I prefer Galois…
The geometry underlying a figure that John Baez
posted four days ago, "A Hypercube of Bits," is
Galois geometry —
See The Galois Tesseract and an earlier
figure from Log24 on May 21, 2007:

For the genesis of the figure,
see The Geometry of Logic.
John Baez at Google+ has an interesting post on crackpots,
dated September 13, 2014.
Related recent material from this journal:
Sense (Sept. 13) and Sensibility (Sept. 14 and later).
See also a New York Times piece from 2009:
Related material:
“You don’t need to eat a whole apple to know it’s rotten.”
— Warren Siegel
“What both cases illustrate, with their fuzzy rhetoric
masking ideological pressure, is a serious moral defect
at the heart of elite culture in America.”
— Ross Douthat in today’s online NY Times
More clarity:
Thanks to John Baez at Google+ for relaying this.
"How do you get young people excited
about space? How do you get them interested
not just in watching movies about space,
or in playing video games set in space …
but in space itself?"
— Megan Garber in The Atlantic , Aug. 16, 2012
One approach:
"There is such a thing as a tesseract" and
Diamond Theory in 1937.
See, too, Baez in this journal.
Here is the link to an MIT Scratch project from the above comment.
See also a comment by a Random Norwegian Dude:

For related art, see
"4D AMBASSADOR (HYPERCUBE)" for Steven H. Cullinane
by the Norwegian artist Josefine Lyche.
"Man of Steel is subversive mythology for atheists
that exalts a Superman who behaves the way they
think God should but doesn’t."
— Jeff Jensen, "Why the Superman of 'Man of Steel'
is the Jesus we wish Jesus would be,"
Entertainment Weekly this afternoon
"He's a bird, he's a plane… He's our savior?"
— Nicole Sperling, "'Man of Steel's' Christian link,"
Los Angeles Times this afternoon
Elsewhere on the Web today:
See also Baez in this journal.
"Mathematics is not the rigid and petrifying schema, as the layman so much likes to view it; with it, we rather stand precisely at the point of intersection of restraint and freedom that makes up the essence of man itself."
— A translated remark by Hermann Weyl, p. 136, "The Current Epistemogical Situation in Mathematics" in Paolo Mancosu (ed.) From Brouwer to Hilbert. The Debate on the Foundations of Mathematics in the 1920s , Oxford University Press, 1998, pp. 123-142, as cited by David Corfield
Corfield once wrote that he would like to know the original German of Weyl's remark. Here it is:
"Die Mathematik ist nicht das starre und Erstarrung bringende Schema, als das der Laie sie so gerne ansieht; sondern wir stehen mit ihr genau in jenem Schnittpunkt von Gebundenheit und Freiheit, welcher das Wesen des Menschen selbst ist."
— Hermann Weyl, page 533 of "Die heutige Erkenntnislage in der Mathematik" (Symposion 1, 1-32, 1925), reprinted in Gesammelte Abhandlungen, Band II (Springer, 1968), pages 511-542
For some context, see a post of January 23, 2006.
John Baez wrote in 1996 ("Week 91") that
"I've never quite seen anyone come right out
and admit that triality arises from the
permutations of the unit vectors i, j, and k
in 3d Euclidean space."
Baez seems to come close to doing this with a
somewhat different i , j , and k — Hurwitz
quaternions— in his 2005 book review
quoted here yesterday.
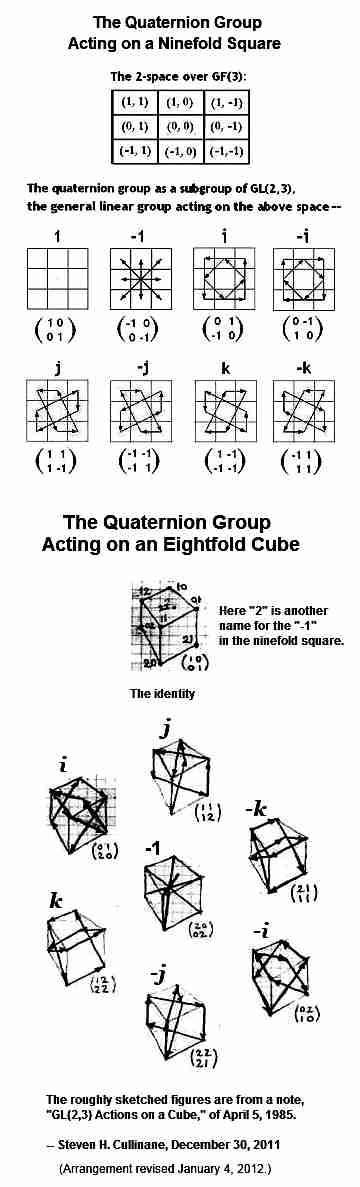
See also the Log24 post of Jan. 4 on quaternions,
and the following figures. The actions on cubes
in the lower figure may be viewed as illustrating
(rather indirectly) the relationship of the quaternion
group's 24 automorphisms to the 24 rotational
symmetries of the cube.
This post continues the April 9 post
commemorating Élie Cartan's birthday.
That post mentioned triality .
Here is John Baez reviewing
On Quaternions and Octonions:
Their Geometry, Arithmetic, and Symmetry
by John H. Conway and Derek A. Smith
(A.K. Peters, Ltd., 2003)—

"In this context, triality manifests itself
as the symmetry that cyclically permutes
the Hurwitz integers i , j , and k ."
Related material— Quaternion Acts in this journal
as well as Finite Geometry and Physical Space.
Grid from a post linked to in yesterday's 24 Hour DeLillo—

For an example of this grid as slow art , consider the following—
"One can show that the binary tetrahedral group
is isomorphic to the special linear group SL(2,3)—
the group of all 2×2 matrices over the finite field F3
with unit determinant." —Wikipedia
As John Baez has noted, these two groups have the same structure as the geometric 24-cell.
For the connection of the grid to the groups and the 24-cell, see Visualizing GL(2,p).
Related material—
The 3×3 grid has been called a symbol of Apollo (Greek god of reason and of the sun).
"This is where we sat through his hushed hour,
a torchlit sky, the closeness of hills barely visible
at high white noon." — Don DeLillo, Point Omega
"… the best way to understand a group is to
see it as the group of symmetries of something."
— John Baez, p. 239, Bulletin (New Series) of the
American Mathematical Society , Vol. 42, No. 2,
April 2005, book review on pp. 229–243
electronically published on January 26, 2005
"Imagine yourself as a gem cutter,
turning around this diamond…."
— Ibid ., p. 240
See also related material from Log24.
A search for some background on Dmitri Tymoczko, the subject of yesterday's evening entry on music theory, shows that his name and mine once both appeared in the same web page— "This Week's Finds in Mathematical Physics (Week 234)," by John Baez, June 12, 2006 (linked to by the Wikipedia article on transformational music theory).
In that page, Baez speculates on the possibility of a connection between music theory and Mathieu groups and says—
"For a pretty explanation of M24, also try this:
Steven H. Cullinane, Geometry of the 4 × 4 square, http://finitegeometry.org/sc/16/geometry.html."
I know of no connection* between the groups I discussed there and music theory. For some background on Tymoczko's work, see the helpful survey "Exploring Musical Space," by Julian Hook (Science magazine, 7 July 2006).
* Apart, that is, from the tesseract (see Geometry of the 4 × 4 Square) shown by Tymoczko in a 2010 lecture—
This is perhaps "Chopin's tesseract" from section 8.5 of Tymoczko's new book
A Geometry of Music (Oxford University Press, 2011).
"These passages suggest that the Form is a character or set of characters
common to a number of things, i.e. the feature in reality which corresponds
to a general word. But Plato also uses language which suggests not only
that the forms exist separately (χωριστά ) from all the particulars, but also
that each form is a peculiarly accurate or good particular of its own kind,
i.e. the standard particular of the kind in question or the model (παράδειγμα )
[i.e. paradigm ] to which other particulars approximate….
… Both in the Republic and in the Sophist there is a strong suggestion
that correct thinking is following out the connexions between Forms.
The model is mathematical thinking, e.g. the proof given in the Meno
that the square on the diagonal is double the original square in area."
— William and Martha Kneale, The Development of Logic,
Oxford University Press paperback, 1985
Plato's paradigm in the Meno —

Changed paradigm in the diamond theorem (2×2 case) —

Aspects of the paradigm change* —
Monochrome figures to
colored figures
Areas to
transformations
Continuous transformations to
non-continuous transformations
Euclidean geometry to
finite geometry
Euclidean quantities to
finite fields
Some pedagogues may find handling all of these
conceptual changes simultaneously somewhat difficult.
* "Paradigm shift " is a phrase that, as John Baez has rightly pointed out,
should be used with caution. The related phrase here was suggested by Plato's
term παράδειγμα above, along with the commentators' specific reference to
the Meno figure that serves as a model. (For "model" in a different sense,
see Burkard Polster.) But note that Baez's own beloved category theory
has been called a paradigm shift.
A new NY Times column:
Today's New York Times
re-edited for philosophers:
See also
John Baez's paper
Duality in Logic and Physics
(for a May 29 meeting at Oxford),
Lubtchansky's Key, with its links
to Duelle (French, f. adj., dual)
and Art Wars for Trotsky's Birthday.
The Magic Lyre
(Click image for context.)
See also Saturday's post—
as well as Solemn Dance
and Mazur at Delphi.
(This last is apparently based on
a talk given by Barry Mazur at Delphi
in 2007 and may or may not appear in
a book, Mathematics and Narrative,
to be published in 2010.)
Suggested tune for the lyre–
"Send me the pillow
that you dream on,"
in memory of Hank Locklin,
who died on this date last year.
From The n-Category Cafe today:
David Corfield at 2:33 PM UTC quoting a chapter from a projected second volume of a biography:
"Grothendieck’s spontaneous reaction to whatever appeared to be causing a difficulty… was to adopt and embrace the very phenomenon that was problematic, weaving it in as an integral feature of the structure he was studying, and thus transforming it from a difficulty into a clarifying feature of the situation."
John Baez at 7:14 PM UTC on research:
"I just don’t want to reinvent a wheel, or waste my time inventing a square one."
For the adoption and embracing of such a problematic phenomenon, see The Square Wheel (this journal, Sept. 14, 2004).
For a connection of the square wheel with yesterday's entry for Julie Taymor's birthday, see a note from 2002:
On May 4, 2005, I wrote a note about how to visualize the 7-point Fano plane within a cube.
Last month, John Baez showed slides that touched on the same topic. This note is to clear up possible confusion between our two approaches.
From Baez’s Rankin Lectures at the University of Glasgow:

The statement is, however, true of the eightfold cube, whose eight subcubes correspond to points of the linear 3-space over the two-element field, if “planes through the origin” is interpreted as planes within that linear 3-space, as in Galois geometry, rather than within the Euclidean cube that Baez’s slides seem to picture.
This Galois-geometry interpretation is, as an article of his from 2001 shows, actually what Baez was driving at. His remarks, however, both in 2001 and 2008, on the plane-cube relationship are both somewhat trivial– since “planes through the origin” is a standard definition of lines in projective geometry– and also unrelated– apart from the possibility of confusion– to my own efforts in this area. For further details, see The Eightfold Cube.
Preview of a Tom Stoppard play presented at Town Hall in Manhattan on March 14, 2008 (Pi Day and Einstein’s birthday):
The play’s title, “Every Good Boy Deserves Favour,” is a mnemonic for the notes of the treble clef EGBDF.
The place, Town Hall, West 43rd Street. The time, 8 p.m., Friday, March 14. One single performance only, to the tinkle– or the clang?– of a triangle. Echoing perhaps the clang-clack of Warsaw Pact tanks muscling into Prague in August 1968.
The “u” in favour is the British way, the Stoppard way, “EGBDF” being “a Play for Actors and Orchestra” by Tom Stoppard (words) and André Previn (music).
And what a play!– as luminescent as always where Stoppard is concerned. The music component of the one-nighter at Town Hall– a showcase for the Boston University College of Fine Arts– is by a 47-piece live orchestra, the significant instrument being, well, a triangle.
When, in 1974, André Previn, then principal conductor of the London Symphony, invited Stoppard “to write something which had the need of a live full-time orchestra onstage,” the 36-year-old playwright jumped at the chance.
One hitch: Stoppard at the time knew “very little about ‘serious’ music… My qualifications for writing about an orchestra,” he says in his introduction to the 1978 Grove Press edition of “EGBDF,” “amounted to a spell as a triangle player in a kindergarten percussion band.”
Review of the same play as presented at Chautauqua Institution on July 24, 2008:
“Stoppard’s modus operandi– to teasingly introduce numerous clever tidbits designed to challenge the audience.”
— Jane Vranish, Pittsburgh Post-Gazette, Saturday, August 2, 2008
“The leader of the band is tired
And his eyes are growing old
But his blood runs through
My instrument
And his song is in my soul.”
— Dan Fogelberg
“He’s watching us all the time.”
| Finnegans Wake, Book II, Episode 2, pp. 296-297: I’ll make you to see figuratleavely the whome of your eternal geomater. And if you flung her headdress on her from under her highlows you’d wheeze whyse Salmonson set his seel on a hexengown.1 Hissss!, Arrah, go on! Fin for fun! 1 The chape of Doña Speranza of the Nacion. |
“…the principle of taking and giving, of learning and teaching, of listening and storytelling, in a word: of reciprocity…. … E. M. Forster famously advised his readers, ‘Only connect.’ ‘Reciprocity’ would be Michael Kruger’s succinct philosophy, with all that the word implies.” — William Boyd, review of Himmelfarb, a novel by Michael Kruger, in The New York Times Book Review, October 30, 1994 Last year’s entry on this date:
The picture above is of the complete graph K6 … Six points with an edge connecting every pair of points… Fifteen edges in all. Diamond theory describes how the 15 two-element subsets of a six-element set (represented by edges in the picture above) may be arranged as 15 of the 16 parts of a 4×4 array, and how such an array relates to group-theoretic concepts, including Sylvester’s synthematic totals as they relate to constructions of the Mathieu group M24. If diamond theory illustrates any general philosophical principle, it is probably the interplay of opposites…. “Reciprocity” in the sense of Lao Tzu. See Reciprocity and Reversal in Lao Tzu. For a sense of “reciprocity” more closely related to Michael Kruger’s alleged philosophy, see the Confucian concept of Shu (Analects 15:23 or 24) described in Kruger’s novel is in part about a Jew: the quintessential Jewish symbol, the star of David, embedded in the K6 graph above, expresses the reciprocity of male and female, as my May 2003 archives illustrate. The star of David also appears as part of a graphic design for cubes that illustrate the concepts of diamond theory: Click on the design for details. Those who prefer a Jewish approach to physics can find the star of David, in the form of K6, applied to the sixteen 4×4 Dirac matrices, in A Graphical Representation The star of David also appears, if only as a heuristic arrangement, in a note that shows generating partitions of the affine group on 64 points arranged in two opposing triplets. Having thus, as the New York Times advises, paid tribute to a Jewish symbol, we may note, in closing, a much more sophisticated and subtle concept of reciprocity due to Euler, Legendre, and Gauss. See |
“Finn MacCool ate the Salmon of Knowledge.”
Wikipedia:
“George Salmon spent his boyhood in Cork City, Ireland. His father was a linen merchant. He graduated from Trinity College Dublin at the age of 19 with exceptionally high honours in mathematics. In 1841 at age 21 he was appointed to a position in the mathematics department at Trinity College Dublin. In 1845 he was appointed concurrently to a position in the theology department at Trinity College Dublin, having been confirmed in that year as an Anglican priest.”
Related material:
Kindergarten Theology,
Arrangements for
56 Triangles.
For more on the
arrangement of
triangles discussed
in Finnegans Wake,
see Log24 on Pi Day,
March 14, 2008.
Happy birthday,
Martin Sheen.
56 Triangles

"This wonderful picture was drawn by Greg Egan with the help of ideas from Mike Stay and Gerard Westendorp. It's probably the best way for a nonmathematician to appreciate the symmetry of Klein's quartic. It's a 3-holed torus, but drawn in a way that emphasizes the tetrahedral symmetry lurking in this surface! You can see there are 56 triangles: 2 for each of the tetrahedron's 4 corners, and 8 for each of its 6 edges."
Exercise:
Click on image for further details.
Note that if eight points are arranged
in a cube (like the centers of the
eight subcubes in the figure above),
there are 56 triangles formed by
the 8 points taken 3 at a time.
John Baez, Week 266
(June 20, 2008):
“The Renaissance thinkers liked to
organize the four elements using
a chain of analogies running
from light to heavy:
fire : air :: air : water :: water : earth
They also organized them
in a diamond, like this:”

This figure of Baez
is related to a saying
attributed to Heraclitus:

For related thoughts by Jung,
see Aion, which contains the
following diagram:

“The formula reproduces exactly the essential features of the symbolic process of transformation. It shows the rotation of the mandala, the antithetical play of complementary (or compensatory) processes, then the apocatastasis, i.e., the restoration of an original state of wholeness, which the alchemists expressed through the symbol of the uroboros, and finally the formula repeats the ancient alchemical tetrameria, which is implicit in the fourfold structure of unity.”
— Carl Gustav Jung
That the words Maximus of Tyre (second century A.D.) attributed to Heraclitus imply a cycle of the elements (analogous to the rotation in Jung’s diagram) is not a new concept. For further details, see “The Rotation of the Elements,” a 1995 webpage by one “John Opsopaus.”
Related material:
Log24 entries of June 9, 2008, and
“Quintessence: A Glass Bead Game,”
by Charles Cameron.
On Spekkens’ toy system and finite geometry
Background–
On finite geometry:
The actions of permutations on a 4 × 4 square in Spekkens’ paper (quant-ph/0401052), and Leifer’s suggestion of the need for a “generalized framework,” suggest that finite geometry might supply such a framework. The geometry in the webpage John cited is that of the affine 4-space over the two-element field.
Related material:
See also arXiv:0707.0074v1 [quant-ph], June 30, 2007:
A fully epistemic model for a local hidden variable emulation of quantum dynamics,
by Michael Skotiniotis, Aidan Roy, and Barry C. Sanders, Institute for Quantum Information Science, University of Calgary. Abstract: "In this article we consider an augmentation of Spekkens’ toy model for the epistemic view of quantum states [1]…."
Hypercube from the Skotiniotis paper:

Reference:
Perimeter Institute for Theoretical Physics, 31 Caroline Street North, Waterloo, Ontario, Canada N2L 2Y5 (Received 11 October 2005; revised 2 November 2006; published 19 March 2007.)
Pennsylvania Lottery
June 26, 2007–
Mid-day 040
Evening 810
A discussion of the work of Ralph Ellison:
"… why do you think he did not finish these novels? He wrote on them for many, many years– 40 years, I think."
"Yes, he worked for 40 years."
See Ellison's novel Juneteenth (New York Times review, 1999)
810:
"But all things then were oracle and secret.
Remember the night when,
lost, returning, we turned back
Confused, and our headlights
singled out the fox?
Our thoughts went with it then,
turning and turning back
With the same terror,
into the deep thicket
Beside the highway,
at home in the dark thicket.
I say the wood within is the dark wood…."
John Baez, Diary, entry of June 22, 2007:
"On Tuesday the 19th….
I hiked down the completely dark but perfectly familiar gravel road with my suitcase in hand, listening to the forest creatures. But then, I couldn't find my parents' driveway! It was embarrassing: I could see their house perfectly well, off in the distance, but it was so darn dark I couldn't spot the driveway. It felt like a dream: after a long flight with many delays, one winds up walking to ones parents house, lost in a spooky forest….
… I sort of enjoy this kind of thing, as long as there's no real danger. It's also sort of scary. The well-lit grid of civilization slowly falls away, and you're out there alone in the night…
Anyway: I considered hiking straight through the woods to my parents' house, but I decided things were already interesting enough, so instead I called my mom and ask her to drive down the driveway a bit, just so I could see where it was. And so she did, and then it was obvious.
So, I got home shortly before midnight. A long and strange day. My dad was already in bed, but I said hi to him anyway."
Related material:

The Crown of Geometry
(according to Logothetti
in a 1980 article)
The crown jewels are the
Platonic solids, with the
icosahedron at the top.
Related material:
"[The applet] Syntheme illustrates ways of partitioning the 12 vertices of an icosahedron into 3 sets of 4, so that each set forms the corners of a rectangle in the Golden Ratio. Each such rectangle is known as a duad. The short sides of a duad are opposite edges of the icosahedron, and there are 30 edges, so there are 15 duads.
Each partition of the vertices into duads is known as a syntheme. There are 15 synthemes; 5 consist of duads that are mutually perpendicular, while the other 10 consist of duads that share a common line of intersection."
— Greg Egan, Syntheme

The above note shows
duads and synthemes related
to the diamond theorem.
See also John Baez's essay
"Some Thoughts on the Number 6."
That essay was written 15 years
ago today– which happens
to be the birthday of
Sir Laurence Olivier, who,
were he alive today, would
be 100 years old.


"Is it safe?"
| From the diary of John Baez: September 22, 2006… Meanwhile, the mystics beckon:
September 23, 2006I’m going up to San Rafael (near the Bay in Northern California) to visit my college pal Bruce Smith and his family. I’ll be back on Wednesday the 27th, just in time to start teaching the next day. |
A check on the Rumi quote yields
this, on a culinary organization:
|
“Out beyond rightdoing and wrongdoing there is a field. I’ll meet you there.”
This is the starting place of good spirit for relationship healing and building prescribed centuries ago in the Middle East by Muslim Sufi teacher and mystic, Jelaluddin Rumi (1207-1273). Even earlier, the Psalmists knew such a meeting place of adversaries was needed, sacred and blessed: |
A Field and a Table:

From “Communications Toolbox”
at MathWorks.com
For more on this field
in a different context, see
Generating the Octad Generator
and
“Putting Descartes Before Dehors”
in my own diary for December 2003.

Descartes

Après l’Office à l’Église
de la Sainte-Trinité, Noël 1890
(After the Service at Holy Trinity Church,
Christmas 1890), Jean Béraud
Let us pray to the Holy Trinity that
San Rafael guides the teaching of John Baez
this year. For related material on theology
and the presence of enemies, see Log24 on
the (former) Feast of San Rafael, 2003.
Baez Link
John Baez’s latest This Week’s Finds
(Week 234, June 12, 2006) has a link
to my “Geometry of the 4×4 Square” at
http://finitegeometry.org/sc/16/geometry.html.
For the next generation:
— Robert A. Heinlein,
The Number of the Beast
Some websites on zeta functions (a classic topic of considerable current interest):
Part I: The 24-Cell
| From John Baez, “This Week’s Finds in Mathematical Physics (Week 198),” September 6, 2003: Noam Elkies writes to John Baez:
The enrapturing discoveries of our field systematically conceal, like footprints erased in the sand, the analogical train of thought that is the authentic life of mathematics – Gian-Carlo Rota |
Like footprints erased in the sand….
“Hello! Kinch here. Put me on to Edenville. Aleph, alpha: nought, nought, one.”
“A very short space of time through very short times of space….
Am I walking into eternity along Sandymount strand?”
— James Joyce, Ulysses, Proteus chapter
A very short space of time through very short times of space….
“It is demonstrated that space-time should possess a discrete structure on Planck scales.”
— Peter Szekeres, abstract of Discrete Space-Time
“A theory…. predicts that space and time are indeed made of discrete pieces.”
— Lee Smolin in Atoms of Space and Time (pdf), Scientific American, Jan. 2004
“… a fundamental discreteness of spacetime seems to be a prediction of the theory….”
— Thomas Thiemann, abstract of Introduction to Modern Canonical Quantum General Relativity
“Theories of discrete space-time structure are being studied from a variety of perspectives.”
— Quantum Gravity and the Foundations of Quantum Mechanics at Imperial College, London
The above speculations by physicists
are offered as curiosities.
I have no idea whether
any of them are correct.
Related material:
Stephen Wolfram offers a brief
History of Discrete Space.
For a discussion of space as discrete
by a non-physicist, see John Bigelow‘s
Space and Timaeus.

A Miniature
Rosetta Stone

John Baez discussed (Sept. 6, 2003) the analogies of Weil, and he himself furnished another such Rosetta stone on a much smaller scale:
“… a 24-element group called the ‘binary tetrahedral group,’ a 24-element group called ‘SL(2,Z/3),’ and the vertices of a regular polytope in 4 dimensions called the ’24-cell.’ The most important fact is that these are all the same thing!”
For further details, see Wikipedia on the 24-cell, on special linear groups, and on Hurwitz quaternions,
The group SL(2,Z/3), also known as “SL(2,3),” is of course derived from the general linear group GL(2,3). For the relationship of this group to the quaternions, see the Log24 entry for August 4 (the birthdate of the discoverer of quaternions, Sir William Rowan Hamilton).
The 3×3 square shown above may, as my August 4 entry indicates, be used to picture the quaternions and, more generally, the 48-element group GL(2,3). It may therefore be regarded as the structure underlying the miniature Rosetta stone described by Baez.
“The typical example of a finite group is GL(n,q), the general linear group of n dimensions over the field with q elements. The student who is introduced to the subject with other examples is being completely misled.”
— J. L. Alperin, book review,
Bulletin (New Series) of the American
Mathematical Society 10 (1984), 121
From Log24,
April 28, 2005:
(See also Log24,
April 5, 2005.)
Compare this diagram with that of
Samuel Beckett in Quad (1981):

Barry Mazur on a seminal paper of algebraist Saunders Mac Lane:
The paper was rejected “because the editor thought that it was ‘more devoid of content’ than any other he had read. ‘Saunders wrote back and said, “That’s the point,”‘ Mazur said. ‘And in some ways that’s the genius of it. It’s the barest, most Beckett-like vocabulary that incorporates the theory and nothing else.'”

“M. de Villepin positively worships Napoleon, and models himself after his hero. In a 600-page biography, Villepin wrote admiringly about the difference between great men like Napoleon and the ‘common run’ of men. It is worth reading every word carefully.
‘Here we touch on that particular essence of great men, on what distinguishes Napoleon or Alexander, Caesar or de Gaulle, from the common run. It is excess, exaltation, and a taste for risk that forms their genius. It is why they are often better understood in their élan by writers and poets, who are possessed of the same thirst for the absolute, than by those who pray at the altar of facts.’
(New Republic)
And in praise of French nationalism, de Villepin wrote,
‘The Gaullist adventure renewed the élan of [Napoleon’s] Consulate through the restoration of a strong executive and the authority of the State, the same scorn for political parties and for compromise, a common taste for action, and an obsession with the general interest and the grandeur of France.’
Those words come straight from 1800. Napoleon’s ‘genius,’ his ‘thirst for the absolute,’ ‘excess, exaltation, and a taste for risk,’ ‘a strong executive and the authority of the State,’ ‘his ‘scorn for political parties and for compromise,’ and ‘an obsession with the grandeur of France’ — it is all classic national hero worship. But today that kind of thinking is used to promote a new vision of destiny, the European Union.”
"Difficult to understand because of intricacy: byzantine, complex, complicated, convoluted, daedal, Daedalian, elaborate, intricate, involute, knotty, labyrinthine, tangled."
— Roget's II: The New Thesaurus, Third Edition

or, The Eightfold Cube

Every permutation of the plane's points that preserves collinearity is a symmetry of the plane. The group of symmetries of the Fano plane is of order 168 and is isomorphic to the group PSL(2,7) = PSL(3,2) = GL(3,2). (See Cameron on linear groups (pdf).)
The above model indicates with great clarity six symmetries of the plane– those it shares with the equilateral triangle. It does not, however, indicate where the other 162 symmetries come from.
Shown below is a new model of this same projective plane, using partitions of cubes to represent points:

The second model is useful because it lets us generate naturally all 168 symmetries of the Fano plane by splitting a cube into a set of four parallel 1x1x2 slices in the three ways possible, then arbitrarily permuting the slices in each of the three sets of four. See examples below.

(Note that this procedure, if regarded as acting on the set of eight individual subcubes of each cube in the diagram, actually generates a group of 168*8 = 1,344 permutations. But the group's action on the diagram's seven partitions of the subcubes yields only 168 distinct results. This illustrates the difference between affine and projective spaces over the binary field GF(2). In a related 2x2x2 cubic model of the affine 3-space over GF(2) whose "points" are individual subcubes, the group of eight translations is generated by interchanges of parallel 2x2x1 cube-slices. This is clearly a subgroup of the group generated by permuting 1x1x2 cube-slices. Such translations in the affine 3-space have no effect on the projective plane, since they leave each of the plane model's seven partitions– the "points" of the plane– invariant.)
To view the cubes model in a wider context, see Galois Geometry, Block Designs, and Finite-Geometry Models.
For another application of the points-as-partitions technique, see Latin-Square Geometry: Orthogonal Latin Squares as Skew Lines.
For more on the plane's symmetry group in another guise, see John Baez on Klein's Quartic Curve and the online book The Eightfold Way. For more on the mathematics of cubic models, see Solomon's Cube.
Black Moses
For an explanation of the title, see
the previous entry and
Robert P. Moses and The Algebra Project.
For another algebra project, see
Log24 entries of April 14-25 as well as
the following “X in a box” figure
from March 10, 2005 and
April 5, 2005.
Those interested in artistic rather than mathematical figures may compare this diagram with that of Samuel Beckett in Quad (1981):

Barry Mazur on a seminal paper of algebraist Saunders Mac Lane:
The paper was rejected “because the editor thought that it was ‘more devoid of content’ than any other he had read. ‘Saunders wrote back and said, “That’s the point,”‘ Mazur said. ‘And in some ways that’s the genius of it. It’s the barest, most Beckett-like vocabulary that incorporates the theory and nothing else.'”
“There are some ideas you simply could not think without a vocabulary to think them.”
Amen.
Beyond Geometry
(Title of current L. A. art exhibit)
|
What is the difference between topology and geometry? Geometry you learn in high school; topology in college. So, topology costs more. A bit more seriously…. |
“The greatest obstacle to discovery
is not ignorance —
it is the illusion of knowledge.”
For the illusion of knowledge,
see (for instance)
The Importance of Being Nothingness,
by Craig J. Hogan
(American Scientist, Sept.-Oct. 2001).
A bit more seriously…
“These cases are
neither harmless nor amusing.”
— Craig J. Hogan, op. cit.
For example:
“Thanks to Dr. Matrix
for honouring this website
with the Award for Science Excellence
on May 14, 2002 and selecting it
for prominent display in the categories
of Mathematics and Creative Minds.”
See also my notes
On Dharwadker’s Attempted Proof,
November 28, 2000, and
The God-Shaped Hole,
February 21, 2001.
Reciprocity
From my entry of Sept. 1, 2003:
"…the principle of taking and giving, of learning and teaching, of listening and storytelling, in a word: of reciprocity….
… E. M. Forster famously advised his readers, 'Only connect.' 'Reciprocity' would be Michael Kruger's succinct philosophy, with all that the word implies."
— William Boyd, review of Himmelfarb, New York Times Book Review, October 30, 1994
Last year's entry on this date:
|
Today's birthday:
"Mathematics is the music of reason."
Sylvester, a nineteenth-century mathematician, coined the phrase "synthematic totals" to describe some structures based on 6-element sets that R. T. Curtis has called "rather unwieldy objects." See Curtis's abstract, Symmetric Generation of Finite Groups, John Baez's essay, Some Thoughts on the Number 6, and my website, Diamond Theory. |
The picture above is of the complete graph
Diamond theory describes how the 15 two-element subsets of a six-element set (represented by edges in the picture above) may be arranged as 15 of the 16 parts of a 4×4 array, and how such an array relates to group-theoretic concepts, including Sylvester's synthematic totals as they relate to constructions of the Mathieu group M24.
If diamond theory illustrates any general philosophical principle, it is probably the interplay of opposites…. "Reciprocity" in the sense of Lao Tzu. See
Reciprocity and Reversal in Lao Tzu.
For a sense of "reciprocity" more closely related to Michael Kruger's alleged philosophy, see the Confucian concept of Shu (Analects 15:23 or 24) described in
Kruger's novel is in part about a Jew: the quintessential Jewish symbol, the star of David, embedded in the
Click on the design for details.
Those who prefer a Jewish approach to physics can find the star of David, in the form of
A Graphical Representation
of the Dirac Algebra.
The star of David also appears, if only as a heuristic arrangement, in a note that shows generating partitions of the affine group on 64 points arranged in two opposing triplets.
Having thus, as the New York Times advises, paid tribute to a Jewish symbol, we may note, in closing, a much more sophisticated and subtle concept of reciprocity due to Euler, Legendre, and Gauss. See
Venn's Trinity
Today is the birthday of logician John Venn.
From the St. Andrews History of Mathematics site:
 "Venn considered three discs R, S, and T as typical subsets of a set U. The intersections of these discs and their complements divide U into 8 non-overlapping regions, the unions of which give 256 different Boolean combinations of the original sets R, S, T."
"Venn considered three discs R, S, and T as typical subsets of a set U. The intersections of these discs and their complements divide U into 8 non-overlapping regions, the unions of which give 256 different Boolean combinations of the original sets R, S, T."
Last night's entry, "A Queer Religion," gave a Catholic view of the Trinity. Here are some less interesting but more fruitful thoughts inspired by Venn's diagram of the Trinity (or, indeed, of any three entities):
"To really know a subject you've got to learn a bit of its history…."
— John Baez, August 4, 2002
"We both know what memories can bring;
They bring diamonds and rust."
— Joan Baez, April 1975
For the "diamonds" brought by memories of the 28 combinations described above, consider how the symmetric group S8 is related to the symmetries of the finite projective space PG(3,2). (See Diamond Theory.)
For the "rust," consider the following:
"Lay not up for yourselves treasures upon earth, where moth and rust doth corrupt…."
— Matthew 6:19
The letters R, U, S, T in the Venn diagram above are perhaps relevant here, symbolizing, if you will, the earthly confusion of language, as opposed to the heavenly clarity of mathematics.
As for MOTH, see the article Hometown Zeroes (which brings us yet again to the Viper Room, scene of River Phoenix's death) and the very skillfully designed website MOTHEMATICS.
Mental Health Month, Day 26:
Part III — Why 26?
At first blush, it seems unlikely that the number 26=2×13, as a product of only two small primes (and those distinct) has any purely mathematical properties of interest. (On the other hand, consider the number 6.) Parts I and II of “Many Dimensions,” notes written earlier today, deal with the struggles of string theorists to justify their contention that a space of 26 dimensions may have some significance in physics. Let them struggle. My question is whether there are any interesting purely mathematical properties of 26, and it turns out, surprisingly, that there are some such properties. All this is a longwinded way of introducing a link to the web page titled “Info on M13,” which gives details of a 1997 paper by J. H. Conway*.
|
“Conway describes the beautiful construction of a discrete mathematical structure which he calls ‘ Why do the simple groups In fact, both the Mathieu group To understand the definition of The points and the lines and the “is-contained-in” relation form an incidence structure over …the 26 objects of the incidence structure [are] 13 points and 13 lines.”
Conway’s construction involves the arrangement, in a circular Levi graph, of 26 marks representing these points and lines, and chords representing the “contains/is contained in” relation. The resulting diagram has a pleasingly symmetric appearance. For further information on the geometry of the number 26, one can look up all primitive permutation groups of degree 26. Conway’s work suggests we look at sets (not just groups) of permutations on n elements. He has shown that this is a fruitful approach for n=13. Whether it may also be fruitful for n=26, I do not know. |
There is no obvious connection to physics, although the physics writer John Baez quoted in my previous two entries shares Conway’s interest in the Mathieu groups.
* J. H. Conway, “M13,” in Surveys in Combinatorics, 1997, edited by R. A. Bailey, London Mathematical Society Lecture Note Series, 241, Cambridge University Press, Cambridge, 1997. 338 pp. ISBN 0 521 59840 0.
Mental Health Month, Day 26:
Many Dimensions,
Part II — The Blue Matrix
But seriously…
John Baez in July 1999:
"…it's really the fact that the Leech lattice is 24-dimensional that lets us compactify 26-dimensional spacetime in such a way as to get a bosonic string theory with the Monster group as symmetries."
Well, maybe. I certainly hope so. If the Leech lattice and the Monster group turn out to have some significance in theoretical physics, then my own work, which deals with symmetries of substructures of the Leech lattice and the Monster, might be viewed in a different light. Meanwhile, I take (cold) comfort from some writers who pursue the "story" theory of truth, as opposed to the "diamond" theory. See the following from my journal:
Evariste Galois and the Rock that Changed Things, and
A Time to Gather Stones Together: Readings for Yom Kippur.
See, too, this web page on Marion Zimmer Bradley's fictional
Matrices, or Blue Star-Stones, and

the purely mathematical site Diamond Theory, which deals with properties of the above "blue matrix" and its larger relatives.
Mental Health Month, Day 26:
John Baez on why bosonic string theory is said to require 26 dimensions —
“By now, if you’re a rigorous sort of pure mathematician, you must be suffering from grave doubts about the sanity of this whole procedure.”
Doubts? Let us just say I prefer
“The G-string is unique in that it combines the properties of all known string theories. It has 26-dimensional modes propagating to the left, 10-dimensional modes propagating to the right, and 2-dimensional modes just sitting around wondering what the hell is going on.”
Today's birthday: James Joseph Sylvester
"Mathematics is the music of reason." — J. J. Sylvester

Sylvester, a nineteenth-century mathematician, coined the phrase "synthematic totals" to describe some structures based on 6-element sets that R. T. Curtis has called "rather unwieldy objects." See Curtis's abstract, Symmetric Generation of Finite Groups, John Baez's essay, Some Thoughts on the Number 6, and my website, Diamond Theory. See also the abstract of a December 7, 2000, talk, Mathematics and the Art of M. C. Escher, in which Curtis notes that graphic designs can "often convey a mathematical idea more eloquently than pages of symbolism."
History, Stephen said….
— To really know a subject you've got to learn a bit of its history….
We both know what memories can bring;
They bring diamonds and rust.
All sorts of structures that can be defined for finite sets have analogues for the projective geometry of finite fields….
Clearly this pattern is trying to tell us something; the question is what. As always, it pays to focus on the simplest case, since that's where everything starts.
In the beginning was the word….
— The Gospel according to Saint John
The anonymous author of John makes liberal use of allegory and double-entendre to illustrate this theme.
Born yesterday: Logician John Venn.
Venn considered three discs R, S, and T as typical subsets of a set U. The intersections of these discs and their complements divide U into 8 nonoverlapping regions….
— History of Mathematics at St. Andrews
Who would not be rapt by the thought of such marvels?….
Powered by WordPress