For a different sort of Lightbox, more closely associated with
the number 13, see instances in this journal of . . .
(Adapted from Encyclopaedia Britannica,
Eleventh Edition (1911), Crystallography .)
"Before time began . . . ." — Optimus Prime
(Adapted from Encyclopaedia Britannica,
Eleventh Edition (1911), Crystallography .)
See also this journal on November 29, 2011 —The Flight from Ennui.
Related illustration from earlier in 2011 —
See also this journal on 20 Sept. 2011 — Relativity Problem Revisited —
as well as Congregated Light.
(Adapted from Encyclopaedia Britannica,
Eleventh Edition (1911), Crystallography .)
Continued … See related previous posts.
Those who prefer narrative to mathematics
may consult Wikipedia on The Cosmic Cube.
|
Monday, May 8, 2017
New Pinterest Board
|
The face at lower left above is that of an early Design edgelord.
A product of that edgelord's school —
See a design by Prince-Ramus in today's New York Times —
Remarks quoted here on the above San Diego date —
A related void —
This afternoon's Windows lockscreen is Badlands National Park —
From this morning's post, a phrase from Schopenhauer —
"Apparent Design in the Fate of the Individual."
An apparent design in the philosophy of Optimus Prime —
"Before time began, there was the Cube" —
Click the image for further remarks.
Continued from April 12, 2022.
"It’s important, as art historian Reinhard Spieler has noted,
that after a brief, unproductive stay in Paris, circa 1907,
Kandinsky chose to paint in Munich. That’s where he formed
the Expressionist art group Der Blaue Reiter (The Blue Rider) —
and where he avoided having to deal with cubism."
— David Carrier,
Remarks by Louis Menand in The New Yorker today —
"The art world isn’t a fixed entity.
It’s continually being reconstituted
as new artistic styles emerge."
(Adapted from Encyclopaedia Britannica,
Eleventh Edition (1911), Crystallography .)
"Before time began, there was the Cube."
— Optimus Prime
See as well Verbum (February 18, 2017).
Related dramatic music —
"Westworld Season 4 begins at Hoover Dam,
with William looking to buy the famous landmark.
What does he consider to be 'stolen' data that is inside?"
| Name Tag | .Space | .Group | .Art |
|---|---|---|---|
| Box4 |
2×2 square representing the four-point finite affine geometry AG(2,2). (Box4.space) |
S4 = AGL(2,2) (Box4.group) |
(Box4.art) |
| Box6 |
3×2 (3-row, 2-column) rectangular array representing the elements of an arbitrary 6-set. |
S6 | |
| Box8 | 2x2x2 cube or 4×2 (4-row, 2-column) array. | S8 or A8 or AGL(3,2) of order 1344, or GL(3,2) of order 168 | |
| Box9 | The 3×3 square. | AGL(2,3) or GL(2,3) | |
| Box12 | The 12 edges of a cube, or a 4×3 array for picturing the actions of the Mathieu group M12. | Symmetries of the cube or elements of the group M12 | |
| Box13 | The 13 symmetry axes of the cube. | Symmetries of the cube. | |
| Box15 |
The 15 points of PG(3,2), the projective geometry of 3 dimensions over the 2-element Galois field. |
Collineations of PG(3,2) | |
| Box16 |
The 16 points of AG(4,2), the affine geometry of 4 dimensions over the 2-element Galois field. |
AGL(4,2), the affine group of |
|
| Box20 | The configuration representing Desargues's theorem. | ||
| Box21 | The 21 points and 21 lines of PG(2,4). | ||
| Box24 | The 24 points of the Steiner system S(5, 8, 24). | ||
| Box25 | A 5×5 array representing PG(2,5). | ||
| Box27 |
The 3-dimensional Galois affine space over the 3-element Galois field GF(3). |
||
| Box28 | The 28 bitangents of a plane quartic curve. | ||
| Box32 |
Pair of 4×4 arrays representing orthogonal Latin squares. |
Used to represent elements of AGL(4,2) |
|
| Box35 |
A 5-row-by-7-column array representing the 35 lines in the finite projective space PG(3,2) |
PGL(3,2), order 20,160 | |
| Box36 | Eurler's 36-officer problem. | ||
| Box45 | The 45 Pascal points of the Pascal configuration. | ||
| Box48 | The 48 elements of the group AGL(2,3). | AGL(2,3). | |
| Box56 |
The 56 three-sets within an 8-set or |
||
| Box60 | The Klein configuration. | ||
| Box64 | Solomon's cube. |
— Steven H. Cullinane, March 26-27, 2022
Related art — The non-Rubik 3x3x3 cube —
The above structure illustrates the affine space of three dimensions
over the three-element finite (i.e., Galois) field, GF(3). Enthusiasts
of Judith Brown's nihilistic philosophy may note the "radiance" of the
13 axes of symmetry within the "central, structuring" subcube.
I prefer the radiance (in the sense of Aquinas) of the central, structuring
eightfold cube at the center of the affine space of six dimensions over
the two-element field GF(2).
The above was suggested by a Log24 review of October 13, 2002,
which in turn suggested a Log24 search for Carousel that yielded
(from Bloomsday Lottery) —
See as well Asimov's "prime radiant," and an illustration
of the number 13 as a radiant prime …
"The Prime Radiant can be adjusted to your mind,
and all corrections and additions can be made
through mental rapport. There will be nothing to
indicate that the correction or addition is yours.
In all the history of the Plan there has been no
personalization. It is rather a creation of all of us
together. Do you understand?"
"Yes, Speaker!"
— Isaac Asimov,
Second Foundation , Ch. 8: Seldon's Plan
"Before time began, there was the Cube."
— Optimus Prime
See also Transformers in this journal.
"For years, the AllSpark rested, sitting dormant
like a giant, useless art installation."
— Vinnie Mancuso at Collider.com yesterday
Related material —
Giant, useless art installation —
Sol LeWitt at MASS MoCA. See also LeWitt in this journal.
(Continued from a remark by art critic Peter Schjeldahl quoted here
last year on New Year's Day in the post "Art as Religion.")
"The unhurried curve got me.
It was like the horizon of a world
that made a non-world of
all of the space outside it."
— Peter Schjeldahl, "Postscript: Ellsworth Kelly,"
The New Yorker , December 30, 2015
This suggests some further material from the paper
that was quoted here yesterday on New Year's Eve —
"In teaching a course on combinatorics I have found
students doubting the existence of a finite projective
plane geometry with thirteen points on the grounds
that they could not draw it (with 'straight' lines)
on paper although they had tried to do so. Such a
lack of appreciation of the spirit of the subject is but
a consequence of the elements of formal geometry
no longer being taught in undergraduate courses.
Yet these students were demanding the best proof of
existence, namely, production of the object described."
— Derrick Breach (See his obituary from 1996.)
A related illustration of the 13-point projective plane
from the University of Western Australia:
Projective plane of order 3
(The four points on the curve
at the right of the image are
the points on the line at infinity .)
The above image is from a post of August 7, 2012,
"The Space of Horizons." A related image —
Click on the above image for further remarks.
Some images from the posts of last July 13
(Harrison Ford's birthday) may serve as funeral
ornaments for the late Prof. David Lavery.
See as well posts on "Silent Snow" and "Starlight Like Intuition."
Notes on space for day 13 of May, 2015 —
The 13 symmetry axes of the cube may be viewed as
the 13 points of the Galois projective space PG(2,3).
This space (a plane) may also be viewed as the nine points
of the Galois affine space AG(2,3) plus the four points on
an added "line at infinity."
Related poetic material:
The ninefold square and Apollo, as well as …
(Five by Five continued)
As the 3×3 grid underlies the order-3 finite projective plane,
whose 13 points may be modeled by
the 13 symmetry axes of the cube,
so the 5×5 grid underlies the order-5 finite projective plane,
whose 31 points may be modeled by
the 31 symmetry axes of the dodecahedron.
See posts tagged Galois-Plane Models.
Update of Nov. 30, 2014 —
For further information on the geometry in
the remarks by Eberhart below, see
pp. 16-17 of A Geometrical Picture Book ,
by Burkard Polster (Springer, 1998). Polster
cites a different article by Lemay.
A search for background to the exercise in the previous post
yields a passage from the late Stephen Eberhart:
|
The first three primes p = 2, 3, and 5 therefore yield finite projective planes with 7, 13, and 31 points and lines, respectively. But these are just the numbers of symmetry axes of the five regular solids, as described in Plato's Timaeus : The tetrahedron has 4 pairs of face planes and corner points + 3 pairs of opposite edges, totalling 7 axes; the cube has 3 pairs of faces + 6 pairs of edges + 4 pairs of corners, totalling 13 axes (the octahedron simply interchanges the roles of faces and corners); and the pentagon dodecahedron has 6 pairs of faces + 15 pairs of edges + 10 pairs of corners, totalling 31 axes (the icosahedron again interchanging roles of faces and corners). This is such a suggestive result, one would expect to find it dealt with in most texts on related subjects; instead, while "well known to those who well know such things" (as Richard Guy likes to quip), it is scarcely to be found in the formal literature [9]. The reason for the common numbers, it turns out, is that the groups of symmetry motions of the regular solids are subgroups of the groups of collineations of the respective finite planes, a face axis being different from an edge axis of a regular solid but all points of a projective plane being alike, so the latter has more symmetries than the former. [9] I am aware only of a series of in-house publications by Fernand Lemay of the Laboratoire de Didactique, Faculté des Sciences de I 'Éducation, Univ. Laval, Québec, in particular those collectively titled Genèse de la géométrie I-X.
— Stephen Eberhart, Dept. of Mathematics, |
Eberhart died of bone cancer in 2003. A memorial by his
high school class includes an Aug. 7, 2003, transcribed
letter from Eberhart to a classmate that ends…
|
… I earned MA’s in math (UW, Seattle) and history (UM, Missoula) where a math/history PhD program had been announced but canceled. So 1984 to 2002 I taught math (esp. non-Euclidean geometry) at C.S.U. Northridge. It’s been a rich life. I’m grateful. Steve |
See also another informative BRIDGES paper by Eberhart
on mathematics and the seven traditional liberal arts.
For previous remarks on this topic, as it relates to
symmetry axes of the cube, see previous posts tagged Interplay.
The above posts discuss, among other things, the Galois
projective plane of order 3, with 13 points and 13 lines.
These Galois points and lines may be modeled in Euclidean geometry
by the 13 symmetry axes and the 13 rotation planes
of the Euclidean cube. They may also be modeled in Galois geometry
by subsets of the 3x3x3 Galois cube (vector 3-space over GF(3)).
The 3×3×3 Galois Cube
Exercise: Is there any such analogy between the 31 points of the
order-5 Galois projective plane and the 31 symmetry axes of the
Euclidean dodecahedron and icosahedron? Also, how may the
31 projective points be naturally pictured as lines within the
5x5x5 Galois cube (vector 3-space over GF(5))?
Update of Nov. 30, 2014 —
For background to the above exercise, see
pp. 16-17 of A Geometrical Picture Book ,
by Burkard Polster (Springer, 1998), esp.
the citation to a 1983 article by Lemay.
“Alexandre Grothendieck est mort jeudi matin
à l’hôpital de Saint-Girons (Ariège), à l’âge de 86 ans.”
Update of 6: 16 PM ET: A memorial of sorts, from May 27 this year:
"… both marveled at early Ingmar Bergman movies."
One of the friends' "humor was inspired by
surrealist painters and Franz Kafka."
"Most of Marvel's fictional characters operate in
a single reality known as the Marvel Universe…."
Related material: The Cosmic Cube.
Surreal requiem for the late Jonathan Winters:
"They 'burn, burn, burn like fabulous yellow roman candles
exploding like spiders across the stars,'
as Jack Kerouac once wrote. It was such a powerful
image that Wal-Mart sells it as a jigsaw puzzle."
— "When the Village Was the Vanguard,"
by Henry Allen, in today's Wall Street Journal
See also Damnation Morning and the picture in
yesterday evening's remarks on art:
The New Yorker on Cubism:
"The style wasn’t new, exactly— or even really a style,
in its purest instances— though it would spawn no end
of novelties in art and design. Rather, it stripped naked
certain characteristics of all pictures. Looking at a Cubist
work, you are forced to see how you see. This may be
gruelling, a gymnasium workout for eye and mind.
It pays off in sophistication."
— Online "Culture Desk" weblog, posted today by Peter Schjeldahl
Non-style from 1911:
See also Cube Symmetry Planes in this journal.
A comment at The New Yorker related to Schjeldahl's phrase "stripped naked"—
"Conceptualism is the least seductive modern-art movement."
POSTED 4/11/2013, 3:54:37 PM BY CHRISKELLEY
(The "conceptualism" link was added to the quoted comment.)
Yesterday's post Permanence dealt with the cube
as a symmetric model of the finite projective plane
PG(2,3), which has 13 points and 13 lines. The points
and lines of the finite geometry occur in the cube as
the 13 axes of symmetry and the 13 planes through
the center perpendicular to those axes. If the three
axes lying in a plane that cuts the cube in a hexagon
are supplemented by the axis perpendicular to that
plane, each plane is associated with four axes and,
dually, each axis is associated with four planes.
My web page on this topic, Cubist Geometries, was
written on February 27, 2010, and first saved to the
Internet Archive on Oct. 4, 2010.
For a more recent treatment of this topic that makes
exactly the same points as the 2010 page, see p. 218
of Configurations from a Graphical Viewpoint , by
Tomaž Pisanski and Brigitte Servatius, published by
Springer on Sept. 23, 2012 (date from both Google
Books and Amazon.com):
For a similar 1998 treatment of the topic, see Burkard Polster's
A Geometrical Picture Book (Springer, 1998), pp. 103-104.
The Pisanski-Servatius book reinforces my argument of Jan. 13, 2013,
that the 13 planes through the cube's center that are perpendicular
to the 13 axes of symmetry of the cube should be called the cube's
symmetry planes , contradicting the usual use of of that term.
That argument concerns the interplay between Euclidean and
Galois geometry. Pisanski and Servatius (and, in 1998, Polster)
emphasize the Euclidean square and cube as guides* to
describing the structure of a Galois space. My Jan. 13 argument
uses Galois structures as a guide to re-describing those of Euclid .
(For a similar strategy at a much more sophisticated level,
see a recent Harvard Math Table.)
Related material: Remarks on configurations in this journal
during the month that saw publication of the Pisanski-Servatius book.
* Earlier guides: the diamond theorem (1978), similar theorems for
2x2x2 (1984) and 4x4x4 cubes (1983), and Visualizing GL(2,p)
(1985). See also Spaces as Hypercubes (2012).
Detail of Sylvie Donmoyer picture discussed
here on January 10—
The "13" tile may refer to the 13 symmetry axes
in the 3x3x3 Galois cube, or the corresponding
13 planes through the center in that cube. (See
this morning's post and Cubist Geometries.)
Today is Wednesday.
O.E. Wodnesdæg "Woden's day," a Gmc. loan-translation of L. dies Mercurii "day of Mercury" (cf. O.N. Oðinsdagr , Swed. Onsdag , O.Fris. Wonsdei , M.Du. Wudensdach ). For Woden , see Odin . — Online Etymology Dictionary
Above: Anthony Hopkins as Odin in the 2011 film "Thor"
Hugo Weaving as Johann Schmidt in the related 2011 film "Captain America"—
"The Tesseract* was the jewel of Odin's treasure room."
Weaving also played Agent Smith in The Matrix Trilogy.
The figure at the top in the circle of 13** "Thor" characters above is Agent Coulson.
"I think I'm lucky that they found out they need somebody who's connected to the real world to help bring these characters all together."
— Clark Gregg, who plays Agent Coulson in "Thor," at UGO.com
For another circle of 13, see the Crystal Skull film implicitly referenced in the Bright Star link from Abel Prize (Friday, Aug. 26, 2011)—
Today's New York Times has a quote about a former mathematician who died on that day (Friday, Aug. 26, 2011)—
"He treated it like a puzzle."
Sometimes that's the best you can do.
* See also tesseract in this journal.
** For a different arrangement of 13 things, see the cube's 13 axes in this journal.
Apollo's 13: A Group Theory Narrative —
I. At Wikipedia —
II. Here —
See Cube Spaces and Cubist Geometries.
The 13 symmetry axes of the (Euclidean) cube–
exactly one axis for each pair of opposite
subcubes in the 27-part (Galois) 3×3×3 cube–
A note from 1985 describing group actions on a 3×3 plane array—
Undated software by Ed Pegg Jr. displays
group actions on a 3×3×3 cube that extend the
3×3 group actions from 1985 described above—
Pegg gives no reference to the 1985 work on group actions.
Margaret Soltan on a summer's-day poem by D.A. Powell—
first, a congregated light, the brilliance of a meadowland in bloom
and then the image must fail, as we must fail, as we
graceless creatures that we are, unmake and befoul our beds
don’t tell me deluge. don’t tell me heat, too damned much heat
"Specifically, your trope is the trope of every life:
the organizing of the disparate parts of a personality
into a self (a congregated light), blazing youth
(a meadowland in bloom), and then the failure
of that image, the failure of that self to sustain itself."
Alternate title for Soltan's commentary, suggested by yesterday's Portrait:
Smart Jewish Girl Fwows Up.
Midrash on Soltan—
Wert thou my enemy, O thou my friend,
How wouldst thou worse, I wonder, than thou dost
Defeat, thwart me?
"…meadow-down is not distressed
For a rainbow footing…."
27
The 13 symmetry axes of the (Euclidean) cube–
exactly one axis for each pair of opposite
subcubes in the 27-part (Galois) 3×3×3 cube–
From yesterday's Seattle Times—
According to police, employees of a Second Avenue mission said the suspect, clad in black and covered in duct tape, had come into the mission "and threatened to blow the place up." He then told staffers "that he was a vampire and wanted to eat people."
The man… also called himself "a space cowboy"….
This suggests two film titles…
and Apollo's 13—
The 13 symmetry axes of the (Euclidean) cube–
exactly one axis for each pair of opposite
subcubes in the (Galois) 3×3×3 cube–
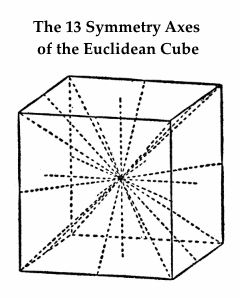
"The cube has…13 axes of symmetry:
6 C2 (axes joining midpoints of opposite edges),
4 C3 (space diagonals), and
3C4 (axes joining opposite face centroids)."
–Wolfram MathWorld article on the cube
These 13 symmetry axes can be used to illustrate the interplay between Euclidean and Galois geometry in a cubic model of the 13-point Galois plane.
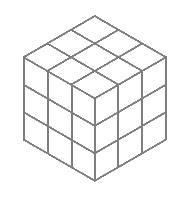
The geometer's 3×3×3 cube–
27 separate subcubes unconnected
by any Rubik-like mechanism–
The 13 symmetry axes of the (Euclidean) cube–
exactly one axis for each pair of opposite
subcubes in the (Galois) 3×3×3 cube–
A closely related structure–
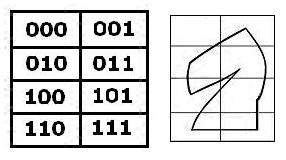
the finite projective plane
with 13 points and 13 lines–
A later version of the 13-point plane
by Ed Pegg Jr.–
A group action on the 3×3×3 cube
as illustrated by a Wolfram program
by Ed Pegg Jr. (undated, but closely
related to a March 26, 1985 note
by Steven H. Cullinane)–
The above images tell a story of sorts.
The moral of the story–
Galois projective geometries can be viewed
in the context of the larger affine geometries
from which they are derived.
The standard definition of points in a Galois projective plane is that they are lines through the (arbitrarily chosen) origin in a corresponding affine 3-space converted to a vector 3-space.
If we choose the origin as the center cube in coordinatizing the 3×3×3 cube (See Weyl's relativity problem ), then the cube's 13 axes of symmetry can, if the other 26 cubes have properly (Weyl's "objectively") chosen coordinates, illustrate nicely the 13 projective points derived from the 27 affine points in the cube model.
The 13 lines of the resulting Galois projective plane may be derived from Euclidean planes through the cube's center point that are perpendicular to the cube's 13 Euclidean symmetry axes.
The above standard definition of points in a Galois projective plane may of course also be used in a simpler structure– the eightfold cube.
(The eightfold cube also allows a less standard way to picture projective points that is related to the symmetries of "diamond" patterns formed by group actions on graphic designs.)
See also Ed Pegg Jr. on finite geometry on May 30, 2006
at the Mathematical Association of America.
More Than Matter
| Wheel in Webster’s Revised Unabridged Dictionary, 1913
(f) Poetry The burden or refrain of a song. ⇒ “This meaning has a low degree of authority, but is supposed from the context in the few cases where the word is found.” Nares. You must sing a-down a-down, An you call him a-down-a. O, how the wheel becomes it! Shak. |
“In one or other of G. F. H. Shadbold’s two published notebooks, Beyond Narcissus and Reticences of Thersites, a short entry appears as to the likelihood of Ophelia’s enigmatic cry: ‘Oh, how the wheel becomes it!’ referring to the chorus or burden ‘a-down, a-down’ in the ballad quoted by her a moment before, the aptness she sees in the refrain.”
— First words of Anthony Powell’s novel “O, How the Wheel Becomes It!” (See Library Thing.)
Related material:
Photo uploaded on January 14, 2009
with caption “This nothing’s more than matter”
and the following nothings from this journal
on the same date– Jan. 14, 2009—
Powered by WordPress
