
Sunday, August 7, 2022
Friday, August 30, 2019
The Coxeter Aleph
The previous post displayed part of a page from
a newspaper published the day Olivia Newton-John
turned 21 — Friday, September 26, 1969.
A meditation, with apologies to Coleridge:
In Xanadu did Newton-John
A stately pleasure-square decree
Where Aleph the sacred symbol ran
Through subsquares measureless to man.
A related video —
Beware, beware, her flashing eyes, her floating hair:
Set design —

As opposed to block design —

Monday, March 31, 2014
Art Wars for Coxeter
Geometer H. S. M. Coxeter died on this date in 2003.
This evening’s daily number from the Keystone state: 822.
Monday, February 20, 2012
Coxeter and the Relativity Problem
In the Beginning…
"As is well known, the Aleph is the first letter of the Hebrew alphabet."
– Borges, "The Aleph" (1945)
From some 1949 remarks of Weyl—
"The relativity problem is one of central significance throughout geometry and algebra and has been recognized as such by the mathematicians at an early time."
— Hermann Weyl, "Relativity Theory as a Stimulus in Mathematical Research," Proceedings of the American Philosophical Society , Vol. 93, No. 7, Theory of Relativity in Contemporary Science: Papers Read at the Celebration of the Seventieth Birthday of Professor Albert Einstein in Princeton, March 19, 1949 (Dec. 30, 1949), pp. 535-541
Weyl in 1946—:
"This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them."
— Hermann Weyl, The Classical Groups , Princeton University Press, 1946, p. 16
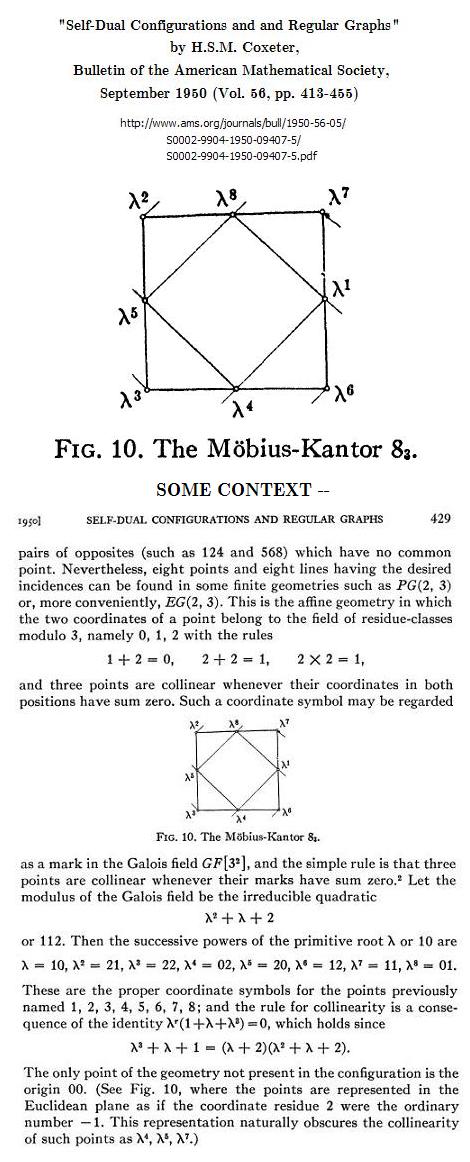
Coxeter in 1950 described the elements of the Galois field GF(9) as powers of a primitive root and as ordered pairs of the field of residue-classes modulo 3—
"… the successive powers of the primitive root λ or 10 are
λ = 10, λ2 = 21, λ3 = 22, λ4 = 02,
λ5 = 20, λ6 = 12, λ7 = 11, λ8 = 01.
These are the proper coordinate symbols….
(See Fig. 10, where the points are represented in the Euclidean plane as if the coordinate residue 2 were the ordinary number -1. This representation naturally obscures the collinearity of such points as λ4, λ5, λ7.)"
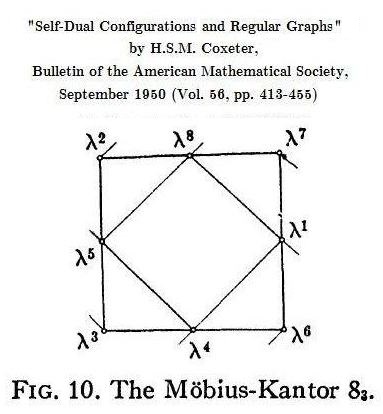
Coxeter's Figure 10 yields...

The Aleph
The details:
Coxeter's phrase "in the Euclidean plane" obscures the noncontinuous nature of the transformations that are automorphisms of the above linear 2-space over GF(3).
Friday, January 7, 2011
Coxeter and the Aleph
In a nutshell —
Epigraph to "The Aleph," a 1945 story by Borges:
O God! I could be bounded in a nutshell,
and count myself a King of infinite space…
— Hamlet, II, 2

The story in book form, 1949
A 2006 biography of geometer H.S.M. Coxeter:

The Aleph (implicit in a 1950 article by Coxeter):

The details:
Related material: Group Actions, 1984-2009.
Thursday, July 8, 2010
Coxeter vs. Fano
The following excerpts from Coxeter's Projective Geometry
sketch his attitude toward geometry in characteristic two.
"… we develop a self-contained account… made
more 'modern' by allowing the field to be general
(though not of characteristic 2) instead of real or complex."
The "modern" in quotation marks may have been an oblique
reference to Segre's Lectures on Modern Geometry (1948, 1961).
(See Coxeter's reference 15 below.)
"It is interesting to see what happens…."
Another thing that happens if 1 + 1 = 0 —
It is no longer true that every finite reflection group
is a Coxeter group (provided we use Chevalley's
fixed-hyperplane definition of "reflection").
Wednesday, August 9, 2023
“The Seed Crystal” — Plan 9 from Science Direct
Thursday, June 29, 2023
Tomb Raider of Geometry
Monday, May 1, 2023
Chain of Title: Complete, Clean, Unencumbered!
From some Canadian legal boilerplate —
E. Be able to provide complete, clean, unencumbered
chain of title for the Project, must have all the rights,
releases and clearances necessary to produce, own and
exploit the Project and for deployment of the Project . . . .
Weak Links in the Chain of Title —
A 2006 biography of geometer H.S.M. Coxeter:
The Aleph (implicit in a 1950 article by Coxeter):
Click on images
for further details.
Wednesday, April 5, 2023
Annals of Artificial Stupidity:
“A Sort of False Coherence”
The "large language model" approach to AI has yielded
startlingly good results for programmers, but is not so good
for finding out facts . . .

A Google search for harvard mathematician h.s.m. coxeter yields . . .

Readers able to use Google can easily find out who wrote the above
gestalt passage. It was not Coxeter.
Further investigation via Google yields the O'Toole source:
O'Toole, Michael, The Language of Displayed Art ,
Leicester University Press, 1994, p. 4.
“A Sort of False Coherence”
Sunday, April 10, 2022
Friday, July 30, 2021
The Secret Subterranean River
The "secret, subterranean river" of Shulevitz is
a flow of thought favorable to the cause of feminism,
but not necessarily to other "revolutionary" ideas.
Compare and contrast:
"Where Alph, the sacred river, ran"
— Coleridge, Kubla Khan
"Where Aleph the sacred symbol ran"
— Cullinane, "The Coxeter Aleph"
For group discussion:
How (if at all) is the "finitude" of Heidegger related to
mathematical finitude and The King of Infinite Space ?
Saturday, July 3, 2021
Here, There, and Chicago
The above phrase "the intersection of storytelling and visual arts"
suggests a review . . .
Storytelling —

Visual arts —

"This pattern is a square divided into nine equal parts.
It has been called the 'Holy Field' division and
was used throughout Chinese history for many
different purposes, most of which were connected
with things religious, political, or philosophical."
– The Magic Square: Cities in Ancient China,
by Alfred Schinz, Edition Axel Menges, 1996, p. 71
A Midrash for Michener —

For a connection of the above "Holy Field"
with pure mathematics, see Coxeter's Aleph.
Friday, December 4, 2020
Devil Music … Now in Infernovision!
“DEVIL – MUSIC
20 pages of incidental music written at school
for G. K. Chesterton’s play MAGIC
by D. Coxeter.”
See also other posts now tagged Infernovision.
Friday, July 5, 2019
The Motive for Metaphor
"János Bolyai was a nineteenth-century mathematician who
set the stage for the field of non-Euclidean geometry."
— Transylvania Now , October 26, 2018
From Coxeter and the Relativity Problem —
Desiring the exhilarations of changes:
The motive for metaphor, shrinking from
The weight of primary noon,
The A B C of being,
The ruddy temper, the hammer
Of red and blue, the hard sound—
Steel against intimation—the sharp flash,
The vital, arrogant, fatal, dominant X.
Friday, April 19, 2019
Pleasantly Discursive Day
” There is a pleasantly discursive treatment
of Pontius Pilate’s unanswered question
‘What is truth?’ ”
— Coxeter, 1987, introduction to Trudeau’s
The Non-Euclidean Revolution
Wednesday, January 2, 2019
“Pleasantly Discursive” Continues.
From this journal on December 13th, 2016 —
" There is a pleasantly discursive treatment
of Pontius Pilate’s unanswered question
‘What is truth?’ "
— Coxeter, 1987, introduction to Trudeau’s
The Non-Euclidean Revolution
Also on December 13th, 2016 —
Saturday, December 22, 2018
Cremona-Richmond
The following are some notes on the history of Clifford algebras
and finite geometry suggested by the "Clifford Modules" link in a
Log24 post of March 12, 2005 —
A more recent appearance of the configuration —
Friday, September 28, 2018
ART WARS Midrash
"When times are mysterious
Serious numbers
Will always be heard."
— Paul Simon,
"When Numbers Get Serious"
"There is a pleasantly discursive treatment of
Pontius Pilate's unanswered question 'What is truth?'"
— H. S. M. Coxeter, introduction to Richard J. Trudeau's remarks
on the "story theory" of truth as opposed to the "diamond theory"
of truth in The Non-Euclidean Revolution (1987)
The deaths of Roth and Grünbaum on September 14th,
The Feast of the Holy Cross, along with Douthat's column
today titled "Only the Truth Can Save Us Now," suggest a
review of …
Monday, May 14, 2018
Space
Tuesday, February 13, 2018
A Titan of the Field
|
On the late Cambridge astronomer Donald Lynden-Bell — "As an academic at a time when students listened and lecturers lectured, he had the disconcerting habit of instead picking on a random undergraduate and testing them on the topic. One former student, now a professor, remembered how he would 'ask on-the-spot questions while announcing that his daughter would solve these problems at the breakfast table'. He got away with it because he was genuinely interested in the work of his colleagues and students, and came to be viewed with great affection by them. He also got away with it because he was well established as a titan of the field." — The London Times on Feb. 8, 2018, at 5 PM (British time) |
Related material —
Two Log24 posts from yesteday, Art Wars and The Void.
See as well the field GF(9) …

… and the 3×3 grid as a symbol of Apollo
(an Olympian rather than a Titan) —
Tuesday, January 9, 2018
Unpleasantly Discursive
Background for the remarks of Koen Thas in the previous post —
Schumacher and Westmoreland, "Modal Quantum Theory" (2010).
Related material —
" There is a pleasantly discursive treatment
of Pontius Pilate’s unanswered question
‘What is truth?’ "
— Coxeter, 1987, introduction to Trudeau’s
The Non-Euclidean Revolution
The whole truth may require an unpleasantly discursive treatment.
Example —
1. The reported death on Friday, Jan. 5, 2018, of a dancer
closely associated with George Balanchine
2. This journal on Friday, Jan. 5, 2018:
3. Illustration from a search related to the above dancer:

4. "Per Mare Per Terras" — Clan slogan above, illustrated with
what looks like a cross-dagger.
"Unsheathe your dagger definitions." — James Joyce.
5. Discursive remarks on quantum theory by the above
Schumacher and Westmoreland:
6. "How much story do you want?" — George Balanchine
Wednesday, August 9, 2017
Implosion
Monday, July 17, 2017
Athens Meets Jerusalem . . .
At the Googleplex .
For those whose only interest in higher mathematics
is as a path to the occult …
Plato's Diamond and the Hebrew letter Aleph —


and some related (if only graphically) mathematics —
Click the above image for some related purely mathematical remarks.
Friday, March 17, 2017
Narrative for Westworld
“That corpse you planted
last year in your garden,
Has it begun to sprout?
Will it bloom this year?
Or has the sudden frost
disturbed its bed?”
— T. S. Eliot, “The Waste Land“
Click the book for a video.
Tuesday, January 3, 2017
Cultist Space
The image of art historian Rosalind Krauss in the previous post
suggests a review of a page from her 1979 essay "Grids" —

The previous post illustrated a 3×3 grid. That cultist space does
provide a place for a few "vestiges of the nineteenth century" —
namely, the elements of the Galois field GF(9) — to hide.
See Coxeter's Aleph in this journal.
Monday, December 19, 2016
Tetrahedral Cayley-Salmon Model
The figure below is one approach to the exercise
posted here on December 10, 2016.

Some background from earlier posts —
Click the image below to enlarge it.
Sunday, December 18, 2016
Two Models of the Small Desargues Configuration
Friday, December 16, 2016
Memory, History, Geometry
These are Rothko's Swamps .
See a Log24 search for related meditations.
For all three topics combined, see Coxeter —
" There is a pleasantly discursive treatment
of Pontius Pilate’s unanswered question
‘What is truth?’ "
— Coxeter, 1987, introduction to Trudeau’s
The Non-Euclidean Revolution
Update of 10 AM ET — Related material, with an elementary example:
Posts tagged "Defining Form." The example —
Tuesday, December 13, 2016
The Thirteenth Novel
John Updike on Don DeLillo's thirteenth novel, Cosmopolis —
" DeLillo’s post-Christian search for 'an order at some deep level'
has brought him to global computerization:
'the zero-oneness of the world, the digital imperative . . . . ' "
— The New Yorker , issue dated March 31, 2003
On that date ….
Related remark —
" There is a pleasantly discursive treatment
of Pontius Pilate’s unanswered question
‘What is truth?’ "
— Coxeter, 1987, introduction to Trudeau’s
The Non-Euclidean Revolution
Tuesday, October 4, 2016
Square Ice
The discovery of "square ice" is discussed in
Nature 519, 443–445 (26 March 2015).
Remarks related, if only by squareness —
this journal on that same date, 26 March 2015 —

The above figure is part of a Log24 discussion of the fact that
adjacency in the set of 16 vertices of a hypercube is isomorphic to
adjacency in the set of 16 subsquares of a square 4×4 array,
provided that opposite sides of the array are identified. When
this fact was first observed, I do not know. It is implicit, although
not stated explicitly, in the 1950 paper by H.S.M. Coxeter from
which the above figure is adapted (blue dots added).
Friday, May 6, 2016
ART WARS continues…

"Again, in spite of that, we call this Friday good."
— T. S. Eliot, Four Quartets
From this journal on Orthodox Good Friday, 2016,
an image from New Scientist on St. Andrew's Day, 2015 —
From an old Dick Tracy strip —

See also meditations from this year's un -Orthodox Good Friday
in a Tennessee weblog and in this journal —
" There is a pleasantly discursive treatment
of Pontius Pilate’s unanswered question
‘What is truth?’ ”
— Coxeter, 1987, introduction to Trudeau’s
The Non-Euclidean Revolution
Friday, March 25, 2016
Pleasantly Discursive
Toronto geometer H.S.M. Coxeter, introducing a book by Unitarian minister
Richard J. Trudeau —
"There is a pleasantly discursive treatment of Pontius Pilate’s
unanswered question ‘What is truth?’”
— Coxeter, 1987, introduction to Trudeau’s
The Non-Euclidean Revolution
Another such treatment …
"Of course, it will surprise no one to find low standards
of intellectual honesty on the Tonight Show.
But we find a less trivial example if we enter the
hallowed halls of Harvard University. . . ."
— Neal Koblitz, "Mathematics as Propaganda"
Less pleasantly and less discursively —
"Funny how annoying a little prick can be."
— The late Garry Shandling
Wednesday, March 2, 2016
A Geometric Glitter
"In the planes that tilt hard revelations on
The eye, a geometric glitter, tiltings …."
— Wallace Stevens, "Someone Puts a Pineapple Together" (1947)
Wednesday, October 21, 2015
Priest Logic for Frodo
Elijah Wood in "The Last Witch Hunter" —

See Graham Priest in this journal.
See also Coxeter + Discursive.
Monday, October 19, 2015
Borromean Generators
From slides dated June 28, 2008 —


Compare to my own later note, from March 4, 2010 —
It seems that Guitart discovered these "A, B, C" generators first,
though he did not display them in their natural setting,
the eightfold cube.
Some context: The epigraph to my webpage
"A Simple Reflection Group of Order 168" —
"Let G be a finite, primitive subgroup of GL(V) = GL(n,D) ,
where V is an n-dimensional vector space over the
division ring D . Assume that G is generated by 'nice'
transformations. The problem is then to try to determine
(up to GL(V) -conjugacy) all possibilities for G . Of course,
this problem is very vague. But it is a classical one,
going back 150 years, and yet very much alive today."
— William M. Kantor, "Generation of Linear Groups,"
pp. 497-509 in The Geometric Vein: The Coxeter Festschrift ,
published by Springer, 1981
Sunday, October 18, 2015
Coordinatization Problem
There are various ways to coordinatize a 3×3 array
(the Chinese "Holy Field'). Here are some —

See Cullinane, Coxeter, and Knight tour.
Thursday, September 17, 2015
A Word to the Wise:
Related material:
From the website of the American Mathematical Society today,
a column by John Baez that was falsely backdated to Sept. 1, 2015 —
Compare and contrast this Baez column
with the posts in the above
Log24 search for "Symplectic."
Updates after 9 PM ET Sept. 17, 2015 —
Related wrinkles in time:
Baez's preceding Visual Insight post, titled
"Tutte-Coxeter Graph," was dated Aug. 15, 2015.
This seems to contradict the AMS home page headline
of Sept. 5, 2015, that linked to Baez's still earlier post
"Heawood Graph," dated Aug. 1. Also, note the
reference in "Tutte-Coxeter Graph" to Baez's related
essay — dated August 17, 2015 —
-
"A Wrinkle in the Mathematical Universe"
at The n-Category Café .
Monday, August 17, 2015
Modern Algebra Illustrated

For illustrations based on the above equations, see
Coxeter and the Relativity Problem and Singer 7-Cycles .
Thursday, July 9, 2015
Man and His Symbols
A post of July 7, Haiku for DeLillo, had a link to posts tagged "Holy Field GF(3)."
As the smallest Galois field based on an odd prime, this structure
clearly is of fundamental importance.

It is, however, perhaps too small to be visually impressive.
A larger, closely related, field, GF(9), may be pictured as a 3×3 array…

|
… hence as the traditional Chinese Holy Field.
Marketing the Holy Field
The above illustration of China's Holy Field occurred in the context of
Log24 posts on Child Buyers. For more on child buyers, see an excellent
condemnation today by Diane Ravitch of the U. S. Secretary of Education.
Saturday, June 13, 2015
Thursday, March 26, 2015
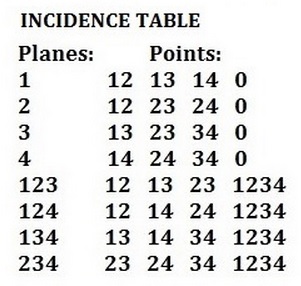
The Möbius Hypercube
The incidences of points and planes in the
Möbius 84 configuration (8 points and 8 planes,
with 4 points on each plane and 4 planes on each point),
were described by Coxeter in a 1950 paper.*
A table from Monday's post summarizes Coxeter's
remarks, which described the incidences in
spatial terms, with the points and planes as the vertices
and face-planes of two mutually inscribed tetrahedra —
Monday's post, "Gallucci's Möbius Configuration,"
may not be completely intelligible unless one notices
that Coxeter has drawn some of the intersections in his
Fig. 24, a schematic representation of the point-plane
incidences, as dotless, and some as hollow dots. The figure,
"Gallucci's version of Möbius's 84," is shown below.
The hollow dots, representing the 8 points (as opposed
to the 8 planes ) of the configuration, are highlighted in blue.

Here a plane (represented by a dotless intersection) contains
the four points that are represented in the square array as lying
in the same row or same column as the plane.
The above Möbius incidences appear also much earlier in
Coxeter's paper, in figures 6 and 5, where they are shown
as describing the structure of a hypercube.
In figures 6 and 5, the dotless intersections representing
planes have been replaced by solid dots. The hollow dots
have again been highlighted in blue.


Figures 6 and 5 demonstrate the fact that adjacency in the set of
16 vertices of a hypercube is isomorphic to adjacency in the set
of 16 subsquares of a square 4×4 array, provided that opposite
sides of the array are identified, as in Fig. 6. The digits in
Coxeter's labels above may be viewed as naming the positions
of the 1's in (0,1) vectors (x4, x3, x2, x1) over the two-element
Galois field.† In that context, the 4×4 array may be called, instead
of a Möbius hypercube , a Galois tesseract .
* "Self-Dual Configurations and Regular Graphs,"
Bulletin of the American Mathematical Society,
Vol. 56 (1950), pp. 413-455
† The subscripts' usual 1-2-3-4 order is reversed as a reminder
that such a vector may be viewed as labeling a binary number
from 0 through 15, or alternately as labeling a polynomial in
the 16-element Galois field GF(24). See the Log24 post
Vector Addition in a Finite Field (Jan. 5, 2013).
Monday, March 23, 2015
Gallucci’s Möbius Configuration
From H. S. M. Coxeter's 1950 paper
"Self-Dual Configurations and Regular Graphs,"
a 4×4 array and a more perspicuous rearrangement—
(Click image to enlarge.)
The above rearrangement brings Coxeter's remarks into accord
with the webpage The Galois Tesseract.
Update of Thursday, March 26, 2015 —
For an explanation of Coxeter's Fig. 24, see Thursday's later
post titled "The Möbius Hypercube."
Sunday, April 13, 2014
Gray Space
Art Wars view —
image from a post at noon on Saturday, April 12:
Kansas City view:
Review of Seeing Gray , a book by pastor Adam Hamilton
of the United Methodist Church of the Resurrection
in Leawood, Kansas, a suburb of Kansas City—
“Adam Hamilton invites us to soulful gray space
between polarities, glorious gray space that is holy,
mysterious, complex, and true. Let us find within
our spirits the courage and humility to live and learn
in this faithful space, to see gray, to discern a more
excellent way.”
—Review by United Methodist Bishop Hope Morgan Ward
The above quotation was suggested by the following from today’s
online Kansas City Star :
“Two of the victims were 14-year-old Reat Griffin Underwood
and his grandfather, William Lewis Corporon, who attended the
United Methodist Church of the Resurrection in Leawood.
The Rev. Adam Hamilton, the church’s senior pastor, shared
the news with church members at the beginning of the evening
Palm Sunday service.”
Update of 10:48 PM — A related photo:

Tuesday, April 1, 2014
For April 1
Monday, March 10, 2014
Strategic Hamlets
From an obituary for a Kennedy advisor
who reportedly died at 94 on February 23, 2014*—
“He favored withdrawing rural civilians
into what he called ‘strategic hamlets’
and spraying defoliants to cut off
the enemy’s food supply.”
Other rhetoric: Hamlet and Infinite Space in this journal,
as well as King of Infinite Space , Part I and Part II.
These “King” links, to remarks on Coxeter and Saniga ,
are about two human beings to whom Hamlet’s
phrase “king of infinite space” has been applied.
The phrase would, of course, be more accurately
applied to God.
* The date of the ‘God’s Architecture’ sermon
at Princeton discussed in this afternoon’s post.
Sunday, March 2, 2014
Sermon
Raiders of the Lost (Continued)
"Socrates: They say that the soul of man is immortal…."
From August 16, 2012—
In the geometry of Plato illustrated below,
"the figure of eight [square] feet" is not , at this point
in the dialogue, the diamond in Jowett's picture.
An 1892 figure by Jowett illustrating Plato's Meno—
A more correct version, from hermes-press.com —
|
Socrates: He only guesses that because the square is double, the line is double.Meno: True.
Socrates: Observe him while he recalls the steps in regular order. (To the Boy.) Tell me, boy, do you assert that a double space comes from a double line? Remember that I am not speaking of an oblong, but of a figure equal every way, and twice the size of this-that is to say of eight feet; and I want to know whether you still say that a double square comes from double line? [Boy] Yes. Socrates: But does not this line (AB) become doubled if we add another such line here (BJ is added)? [Boy] Certainly.
Socrates: And four such lines [AJ, JK, KL, LA] will make a space containing eight feet? [Boy] Yes. Socrates: Let us draw such a figure: (adding DL, LK, and JK). Would you not say that this is the figure of eight feet? [Boy] Yes. Socrates: And are there not these four squares in the figure, each of which is equal to the figure of four feet? (Socrates draws in CM and CN) [Boy] True. Socrates: And is not that four times four? [Boy] Certainly. Socrates: And four times is not double? [Boy] No, indeed. Socrates: But how much? [Boy] Four times as much. Socrates: Therefore the double line, boy, has given a space, not twice, but four times as much. [Boy] True. Socrates: Four times four are sixteen— are they not? [Boy] Yes. |
As noted in the 2012 post, the diagram of greater interest is
Jowett's incorrect version rather than the more correct version
shown above. This is because the 1892 version inadvertently
illustrates a tesseract:
A 4×4 square version, by Coxeter in 1950, of a tesseract—
This square version we may call the Galois tesseract.
Saturday, January 4, 2014
For Phil Everly
A Souther song at YouTube.
See also the lyrics and, in this journal,
synchronicity on the uploading date.
Related art —
End of the Line Blues

Saturday, November 16, 2013
Raiders of the Lost Theorem

Yes. See …
The 48 actions of GL(2,3) on a 3×3 coordinate-array A,
when matrices of that group right-multiply the elements of A,
with A =
| (1,1) (1,0) (1,2) (0,1) (0,0) (0,2) (2,1) (2,0) (2,2) |
Actions of GL(2,p) on a pxp coordinate-array have the
same sorts of symmetries, where p is any odd prime.
Note that A, regarded in the Sallows manner as a magic square,
has the constant sum (0,0) in rows, columns, both diagonals, and
all four broken diagonals (with arithmetic modulo 3).
For a more sophisticated approach to the structure of the
ninefold square, see Coxeter + Aleph.
Tuesday, November 12, 2013
Soundtrack
“DEVIL – MUSIC
20 pages of incidental music written at school
for G. K. Chesterton’s play MAGIC
by D. Coxeter.”
See also…
Related material — Chesterton + Magic in this journal.
Thursday, November 7, 2013
Pattern Grammar
Yesterday afternoon's post linked to efforts by
the late Robert de Marrais to defend a mathematical
approach to structuralism and kaleidoscopic patterns.
Two examples of non-mathematical discourse on
such patterns:
1. A Royal Society paper from 2012—
Click the above image for related material in this journal.
2. A book by Junichi Toyota from 2009—
Kaleidoscopic Grammar: Investigation into the Nature of Binarism
I find such non-mathematical approaches much less interesting
than those based on the mathematics of reflection groups .
De Marrais described the approaches of Vladimir Arnold and,
earlier, of H. S. M. Coxeter, to such groups. These approaches
dealt only with groups of reflections in Euclidean spaces.
My own interest is in groups of reflections in Galois spaces.
See, for instance, A Simple Reflection Group of Order 168.
Galois spaces over fields of characteristic 2 are particularly
relevant to what Toyota calls binarism .
Tuesday, August 13, 2013
The Story of N
(Continued from this morning)

The above stylized "N," based on
an 8-cycle in the 9-element Galois field
GF(9), may also be read as an Aleph.
Graphic designers may prefer a simpler,
bolder version:

Wednesday, July 24, 2013
The Broken Tablet
This post was suggested by a search for the
Derridean phrase "necessary possibility"* that
led to web pages on a conference at Harvard
on Friday and Saturday, March 26**-27, 2010,
on Derrida and Religion .
The conference featured a talk titled
"The Poetics of the Broken Tablet."

I prefer the poetics of projective geometry.
An illustration— The restoration of the full
15-point "large" Desargues configuration in
place of the diminished 10-point Desargues
configuration that is usually discussed.
Click on the image for further details.
* See a discussion of this phrase in
the context of Brazilian religion.
** See also my own philosophical reflections
on Friday, March 26, 2010:
"You Can't Make This Stuff Up."
Tuesday, May 14, 2013
Raiders of the Lost Aleph
See Coxeter + Aleph in this journal.
Epigraph to "The Aleph," a 1945 story by Borges:
"O God! I could be bounded in a nutshell,
and count myself a King of infinite space…"
– Hamlet, II, 2
Friday, April 19, 2013
The Large Desargues Configuration
Desargues' theorem according to a standard textbook:
"If two triangles are perspective from a point
they are perspective from a line."
The converse, from the same book:
"If two triangles are perspective from a line
they are perspective from a point."
Desargues' theorem according to Wikipedia
combines the above statements:
"Two triangles are in perspective axially [i.e., from a line]
if and only if they are in perspective centrally [i.e., from a point]."
A figure often used to illustrate the theorem,
the Desargues configuration , has 10 points and 10 lines,
with 3 points on each line and 3 lines on each point.
A discussion of the "if and only if" version of the theorem
in light of Galois geometry requires a larger configuration—
15 points and 20 lines, with 3 points on each line
and 4 lines on each point.
This large Desargues configuration involves a third triangle,
needed for the proof (though not the statement ) of the
"if and only if" version of the theorem. Labeled simply
"Desargues' Theorem," the large configuration is the
frontispiece to Volume I (Foundations) of Baker's 6-volume
Principles of Geometry .
Point-line incidence in this larger configuration is,
as noted in a post of April 1, 2013, described concisely
by 20 Rosenhain tetrads (defined in 1905 by
R. W. H. T. Hudson in Kummer's Quartic Surface ).
The third triangle, within the larger configuration,
is pictured below.
Monday, April 1, 2013
Desargues via Rosenhain
Background: Rosenhain and Göpel Tetrads in PG(3,2)
|
Introduction: The Large Desargues Configuration Added by Steven H. Cullinane on Friday, April 19, 2013 Desargues' theorem according to a standard textbook:
"If two triangles are perspective from a point The converse, from the same book:
"If two triangles are perspective from a line
Desargues' theorem according to Wikipedia
"Two triangles are in perspective axially [i.e., from a line]
A figure often used to illustrate the theorem,
A discussion of the "if and only if" version of the theorem
This large Desargues configuration involves a third triangle,
Point-line incidence in this larger configuration is,
The third triangle, within the larger configuration,
|

A connection discovered today (April 1, 2013)—
(Click to enlarge the image below.)
Update of April 18, 2013
Note that Baker's Desargues-theorem figure has three triangles,
ABC, A'B'C', A"B"C", instead of the two triangles that occur in
the statement of the theorem. The third triangle appears in the
course of proving, not just stating, the theorem (or, more precisely,
its converse). See, for instance, a note on a standard textbook for
further details.
(End of April 18, 2013 update.)
Update of April 14, 2013
See Baker's Proof (Edited for the Web) for a detailed explanation
of the above picture of Baker's Desargues-theorem frontispiece.
(End of April 14, 2013 update.)
Update of April 12, 2013
A different figure, from a site at National Tsing Hua University,
shows the three triangles of Baker's figure more clearly:
(End of update of April 12, 2013)
Update of April 13, 2013
Another in a series of figures illustrating
Desargues's theorem in light of Galois geometry:

See also the original Veblen-Young figure in context.
(End of update of April 13, 2013)

Rota's remarks, while perhaps not completely accurate, provide some context
for the above Desargues-Rosenhain connection. For some other context,
see the interplay in this journal between classical and finite geometry, i.e.
between Euclid and Galois.
For the recent context of the above finite-geometry version of Baker's Vol. I
frontispiece, see Sunday evening's finite-geometry version of Baker's Vol. IV
frontispiece, featuring the Göpel, rather than the Rosenhain, tetrads.
For a 1986 illustration of Göpel and Rosenhain tetrads (though not under
those names), see Picturing the Smallest Projective 3-Space.
In summary… the following classical-geometry figures
are closely related to the Galois geometry PG(3,2):
|
Volume I of Baker's Principles has a cover closely related to the Rosenhain tetrads in PG(3,2) |
Volume IV of Baker's Principles has a cover closely related to the Göpel tetrads in PG(3,2) |
|
Foundations (click to enlarge)
|
Higher Geometry (click to enlarge)
|
Saturday, March 16, 2013
The Crosswicks Curse
From the prologue to the new Joyce Carol Oates
novel Accursed—
"This journey I undertake with such anticipation
is not one of geographical space but one of Time—
for it is the year 1905 that is my destination.
1905!—the very year of the Curse."
Today's previous post supplied a fanciful link
between the Crosswicks Curse of Oates and
the Crosswicks tesseract of Madeleine L'Engle.
The Crosswicks Curse according to L'Engle
in her classic 1962 novel A Wrinkle in Time —
"There is such a thing as a tesseract."
A tesseract is a 4-dimensional hypercube that
(as pointed out by Coxeter in 1950) may also
be viewed as a 4×4 array (with opposite edges
identified).
Meanwhile, back in 1905…
For more details, see how the Rosenhain and Göpel tetrads occur naturally
in the diamond theorem model of the 35 lines of the 15-point projective
Galois space PG(3,2).
See also Conwell in this journal and George Macfeely Conwell in the
honors list of the Princeton Class of 1905.
Saturday, January 5, 2013
Vector Addition in a Finite Field
The finite (i.e., Galois) field GF(16),
according to J. J. Seidel in 1974—
The same field according to Steven H. Cullinane in 1986,
in its guise as the affine 4-space over GF(2)—

The same field, again disguised as an affine 4-space,
according to John H. Conway and N.J.A. Sloane in
Sphere Packings, Lattices, and Groups , first published in 1988—

The above figure by Conway and Sloane summarizes, using
a 4×4 array, the additive vector-space structure of the finite
field GF(16).
This structure embodies what in Euclidean space is called
the parallelogram rule for vector addition—

(Thanks to June Lester for the 3D (uvw) part of the above figure.)
For the transition from this colored Euclidean hypercube
(used above to illustrate the parallelogram rule) to the
4×4 Galois space (illustrated by Cullinane in 1979 and
Conway and Sloane in 1988— or later… I do not have
their book’s first edition), see Diamond Theory in 1937,
Vertex Adjacency in a Tesseract and in a 4×4 Array,
Spaces as Hypercubes, and The Galois Tesseract.
For some related narrative, see tesseract in this journal.
(This post has been added to finitegeometry.org.)
Update of August 9, 2013—
Coordinates for hypercube vertices derived from the
parallelogram rule in four dimensions were better
illustrated by Jürgen Köller in a web page archived in 2002.
Update of August 13, 2013—
The four basis vectors in the 2002 Köller hypercube figure
are also visible at the bottom of the hypercube figure on
page 7 of “Diamond Theory,” excerpts from a 1976 preprint
in Computer Graphics and Art , Vol. 2, No. 1, February 1977.
A predecessor: Coxeter’s 1950 hypercube figure from
“Self-Dual Configurations and Regular Graphs.”
Saturday, December 22, 2012
Web Links:
Spidey Goes to Church
More realistically…
- "Nick Bostrom … is a Swedish philosopher at
St. Cross College, University of Oxford…." - "The early location of St Cross was on a site in
St Cross Road, immediately south of St Cross Church." - "The church building is located on St Cross Road
just south of Holywell Manor." - "Balliol College has had a presence in the area since
the purchase by Benjamin Jowett, the Master, in the 1870s
of the open area which is the Balliol sports ground
'The Master's Field.' " - Leaving Wikipedia, we find a Balliol field at Log24:

- A different view of the same field, from 1950—
 .
. - A view from 1974, thanks to J. J. Seidel —

- Yesterday's Analogies.
Sunday, December 9, 2012
Eve’s Menorah
"Now the serpent was more subtle
than any beast of the field…."
— Genesis 3:1
"“The serpent’s eyes shine
As he wraps around the vine….”
– Don Henley
"Nine is a vine."
— Folk rhyme
Click images for some background.
Tuesday, November 27, 2012
Counterexample
The non-Coxeter simple reflection group of order 168
is a counterexample to the statement that
"Every finite reflection group is a Coxeter group."
The counterexample is based on a definition of "reflection group"
that includes reflections defined over finite fields.
Today I came across a 1911 paper that discusses the counterexample.
Of course, Coxeter groups were undefined in 1911, but the paper, by
Howard H. Mitchell, discusses the simple order-168 group as a reflection group .
(Naturally, Mitchell's definition of "reflection" and his statement that
"The discussion of the binary groups
applies also to the case p = 2."
should be approached with care.)
A review of this topic might be appropriate for Jessica Fintzen's 2012 fall tutorial at Harvard
on reflection groups and Coxeter groups. The syllabus for the tutorial states that
"finite Coxeter groups correspond precisely to finite reflection groups." This statement
is based on Fintzen's definition of "reflection group"—
"Reflection groups are— as their name indicates—
groups generated by reflections across
hyperplanes of Rn which contain the origin."
For some background, see William Kantor's 1981 paper "Generation of Linear Groups"
(quoted at the finitegeometry.org page on the simple order-168 counterexample).
Kantor discusses Mitchell's work in some detail, but does not mention the
simple order-168 group explicitly.
Tuesday, October 16, 2012
Cube Review
Last Wednesday's 11 PM post mentioned the
adjacency-isomorphism relating the 4-dimensional
hypercube over the 2-element Galois field GF(2) to
the 4×4 array made up of 16 square cells, with
opposite edges of the 4×4 array identified.
A web page illustrates this property with diagrams that
enjoy the Karnaugh property— adjacent vertices, or cells,
differ in exactly one coordinate. A brief paper by two German
authors relates the Karnaugh property to the construction
of a magic square like that of Dürer (see last Wednesday).
In a similar way (search the Web for Karnaugh + cube ),
vertex adjacency in the 6-dimensional hypercube over GF(2)
is isomorphic to cell adjacency in the 4x4x4 cube, with
opposite faces of the 4x4x4 cube identified.
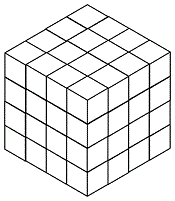
The above cube may be used to illustrate some properties
of the 64-point Galois 6-space that are more advanced
than those studied by enthusiasts of "magic" squares
and cubes.
See
- the 4x4x4 cube and An Invariance of Symmetry
- the 4x4x4 cube and the nineteenth-century
geometers' "Solomon's seal" - the 4x4x4 cube and the Kummer surface
- the 4x4x4 cube and the Klein quadric.
Those who prefer narrative to mathematics may
consult posts in this journal containing the word "Cuber."
Thursday, September 27, 2012
Kummer and the Cube
Denote the d-dimensional hypercube by
"… after coloring the sixty-four vertices of
alternately red and blue, we can say that
the sixteen pairs of opposite red vertices represent
the sixteen nodes of Kummer's surface, while
the sixteen pairs of opposite blue vertices
represent the sixteen tropes."
— From "Kummer's 166 ," section 12 of Coxeter's 1950
"Self-dual Configurations and Regular Graphs"
Just as the 4×4 square represents the 4-dimensional
hypercube
so the 4x4x4 cube represents the 6-dimensional
hypercube
For religious interpretations, see
Nanavira Thera (Indian) and
I Ching geometry (Chinese).
See also two professors in The New York Times
discussing images of the sacred in an op-ed piece
dated Sept. 26 (Yom Kippur).
Wednesday, September 19, 2012
Art Wars (continued)
Today's previous post, "For Odin's Day," discussed
a mathematical object, the tesseract, from a strictly
narrative point of view.
In honor of George Balanchine, Odin might yield the
floor this evening to Apollo.
From a piece in today's online New York Times titled
"How a God Finds Art (the Abridged Version)"—
"… the newness at the heart of this story,
in which art is happening for the first time…."
Some related art—
and, more recently—
This more recent figure is from Ian Stewart's 1996 revision
of a 1941 classic, What Is Mathematics? , by Richard Courant
and Herbert Robbins.
Apollo might discuss with Socrates how the confused slave boy
of Plato's Meno would react to Stewart's remark that
"The number of copies required to double an
object's size depends on its dimension."
Apollo might also note an application of Socrates' Meno diagram
to the tesseract of this afternoon's Odin post—
Thursday, August 16, 2012
Raiders of the Lost Tesseract
(Continued from August 13. See also Coxeter Graveyard.)
Here the tombstone says
"GEOMETRY… 600 BC — 1900 AD… R.I.P."
In the geometry of Plato illustrated below,
"the figure of eight [square] feet" is not , at this point
in the dialogue, the diamond in Jowett's picture.
An 1892 figure by Jowett illustrating Plato's Meno—
Jowett's picture is nonetheless of interest for
its resemblance to a figure drawn some decades later
by the Toronto geometer H. S. M. Coxeter.
A similar 1950 figure by Coxeter illustrating a tesseract—
For a less scholarly, but equally confusing, view of the number 8,
see The Eight , a novel by Katherine Neville.
Sunday, July 29, 2012
The Galois Tesseract
The three parts of the figure in today's earlier post "Defining Form"—

— share the same vector-space structure:
| 0 | c | d | c + d |
| a | a + c | a + d | a + c + d |
| b | b + c | b + d | b + c + d |
| a + b | a + b + c | a + b + d | a + b + c + d |
(This vector-space a b c d diagram is from Chapter 11 of
Sphere Packings, Lattices and Groups , by John Horton
Conway and N. J. A. Sloane, first published by Springer
in 1988.)
The fact that any 4×4 array embodies such a structure was implicit in
the diamond theorem (February 1979). Any 4×4 array, regarded as
a model of the finite geometry AG(4, 2), may be called a Galois tesseract.
(So called because of the Galois geometry involved, and because the
16 cells of a 4×4 array with opposite edges identified have the same
adjacency pattern as the 16 vertices of a tesseract (see, for instance,
Coxeter's 1950 "Self-Dual Configurations and Regular Graphs," figures
5 and 6).)
A 1982 discussion of a more abstract form of AG(4, 2):

Source:

The above 1982 remarks by Brouwer may or may not have influenced
the drawing of the above 1988 Conway-Sloane diagram.
Friday, July 27, 2012
Olympics Special
Thursday, June 21, 2012
Lesson
From Tony Rothman's review of a 2006 book by
Siobhan Roberts—
"The most engaging aspect of the book is its
chronicle of the war between geometry and algebra,
which pits Coxeter, geometry's David, against
Nicolas Bourbaki, algebra's Goliath."
The conclusion of Rothman's review—
"There is a lesson here."
Related material: a search for Galois geometry .
Tuesday, May 1, 2012
What is Truth? (continued)
"There is a pleasantly discursive treatment of
Pontius Pilate's unanswered question 'What is truth?'"
— H. S. M. Coxeter, 1987
Returning to the Walpurgisnacht posts
Decomposition (continued) and
Decomposition– Part III —
Some further background…
SAT
(Not a Scholastic Aptitude Test)
"In computer science, satisfiability (often written
in all capitals or abbreviated SAT) is the problem
of determining if the variables of a given Boolean
formula can be assigned in such a way as to
make the formula evaluate to TRUE."
— Wikipedia article Boolean satisfiability problem
For the relationship of logic decomposition to SAT,
see (for instance) these topics in the introduction to—
Advanced Techniques in Logic Synthesis,
Optimizations and Applications* —
Click image for a synopsis.
* Edited by Sunil P. Khatri and Kanupriya Gulati
Thursday, April 5, 2012
Tuesday, February 14, 2012
The Ninth Configuration
The showmanship of Nicki Minaj at Sunday's
Grammy Awards suggested the above title,
that of a novel by the author of The Exorcist .
The Ninth Configuration —
The ninth* in a list of configurations—
"There is a (2d-1)d configuration
known as the Cox configuration."
— MathWorld article on "Configuration"
For further details on the Cox 326 configuration's Levi graph,
a model of the 64 vertices of the six-dimensional hypercube γ6 ,
see Coxeter, "Self-Dual Configurations and Regular Graphs,"
Bull. Amer. Math. Soc. Vol. 56, pages 413-455, 1950.
This contains a discussion of Kummer's 166 as it
relates to γ6 , another form of the 4×4×4 Galois cube.

See also Solomon's Cube.
* Or tenth, if the fleeting reference to 113 configurations is counted as the seventh—
and then the ninth would be a 153 and some related material would be Inscapes.
Tuesday, January 31, 2012
Tesseract
|
"… a finite set with n elements Tesseract formed from a 4-set—
The same 16 subsets or points can
"There is such a thing as a 4-set." |
Update of August 12, 2012:
Figures like the above, with adjacent vertices differing in only one coordinate,
appear in a 1950 paper of H. S. M. Coxeter—
Saturday, January 28, 2012
The Sweet Smell of Avon
The twin topics of autism and of narrowing definitions
suggested the following remarks.
The mystical number "318" in the pilot episode
of Kiefer Sutherland's new series about autism, "Touch,"
is so small that it can easily apply (as the pilot
illustrated) to many different things: a date, a
time, a bus number, an address, etc.
The last 3/18 Log24 post— Defining Configurations—
led, after a false start and some further research,
to the writing of the webpage Configurations and Squares.
An image from that page—

Interpreting this, in an autistic manner, as the number
287501346 lets us search for more specific items
than those labeled simply 318.
The search yields, among other things, an offer of
Night Magic Cologne (unsold)—
For further mystery and magic, see, from the date
the Night Magic offer closed— May 8, 2010— "A Better Story."
See also the next day's followup, "The Ninth Gate."
Sunday, January 1, 2012
Sunday Shul
"… myths are stories, and like all narratives
they unravel through time, whereas grids
are not only spatial to start with,
they are visual structures that explicitly reject
a narrative or sequential reading of any kind."
— Rosalind Krauss in "Grids,"
October (Summer 1979), 9: 50-64.
Counterexample—

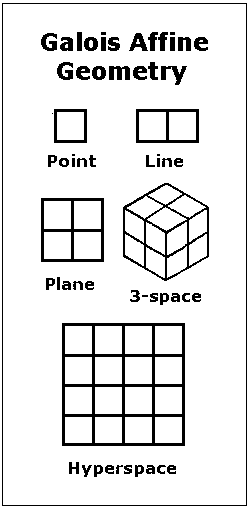
The Ninefold Square
See Coxeter and the Aleph and Ayn Sof—
| Mathematics and Narrative, Illustrated |
|
 Mathematics |
 Narrative |
Friday, November 18, 2011
Hypercube Rotations
The hypercube has 192 rotational symmetries.
Its full symmetry group, including reflections,
is of order 384.
See (for instance) Coxeter—

Related material—
The rotational symmetry groups of the Platonic solids
(from April 25, 2011)—

— and the figure in yesterday evening's post on the hypercube—

(Animation source: MIQEL.com)
Clearly hypercube rotations of this sort carry any
of the eight 3D subcubes to the central subcube
of a central projection of the hypercube—

The 24 rotational symmeties of that subcube induce
24 rigid rotations of the entire hypercube. Hence,
as in the logic of the Platonic symmetry groups
illustrated above, the hypercube has
rotational symmetries.
Thursday, October 20, 2011
The Thing Itself
Suggested by an Oct. 18 piece in the Book Bench section
of the online New Yorker magazine—
Related material suggested by the "Shouts and Murmurs" piece
in The New Yorker , issue dated Oct. 24, 2011—
"a series of e-mails from a preschool teacher planning to celebrate
the Day of the Dead instead of Halloween…"
A search for Coxeter + Graveyard in this journal yields…
Here the tombstone says "GEOMETRY… 600 BC — 1900 AD… R.I.P."
A related search for Plato + Tombstone yields an image from July 6, 2007…

Here Plato's poems to Aster suggested
the "Star and Diamond" tombstone.
The eight-rayed star is an ancient symbol of Venus
and the diamond is from Plato's Meno .
The star and diamond are combined in a figure from
12 AM on September 6th, 2011—
The Diamond Star

See Configurations and Squares.
That webpage explains how Coxeter
united the diamond and the star.
Those who prefer narrative to mathematics may consult
a definition of the Spanish word lucero from March 28, 2003.
Monday, October 10, 2011
10/10
See last year's Day of the Tetraktys.
Those who prefer Hebrew to Greek may consult Coxeter and the Aleph.
See also last midnight's The Aleph as well as Saturday morning's
An Ordinary Evening in Hartford and Saturday evening's
For Whom the Bell (with material from March 20, 2011).
For connoisseurs of synchronicity, there is …
THE LAST CONCERT
Cached from http://mrpianotoday.com/tourdates.htm —
The last concert of Roger Williams — March 20, 2011 —
|
March 20 |
"Roger Williams" In Concert, |
Palm Desert, CA |
Background music… Theme from "Somewhere in Time"
Thursday, September 8, 2011
Starring the Diamond
"In any geometry satisfying Pappus's Theorem,
the four pairs of opposite points of 83
are joined by four concurrent lines."
— H. S. M. Coxeter (see below)
Continued from Tuesday, Sept. 6—
The Diamond Star

The above is a version of a figure from Configurations and Squares.
Yesterday's post related the the Pappus configuration to this figure.
Coxeter, in "Self-Dual Configurations and Regular Graphs," also relates Pappus to the figure.
Some excerpts from Coxeter—

The relabeling uses the 8 superscripts
from the first picture above (plus 0).
The order of the superscripts is from
an 8-cycle in the Galois field GF(9).
The relabeled configuration is used in a discussion of Pappus—

(Update of Sept. 10, 2011—
Coxeter here has a note referring to page 335 of
G. A. Miller, H. F. Blichfeldt, and L. E. Dickson,
Theory and Applications of Finite Groups , New York, 1916.)
Coxeter later uses the the 3×3 array (with center omitted) again to illustrate the Desargues configuration—

The Desargues configuration is discussed by Gian-Carlo Rota on pp. 145-146 of Indiscrete Thoughts—
"The value of Desargues' theorem and the reason why the statement of this theorem has survived through the centuries, while other equally striking geometrical theorems have been forgotten, is in the realization that Desargues' theorem opened a horizon of possibilities that relate geometry and algebra in unexpected ways."
Sunday, August 28, 2011
The Cosmic Part
Yesterday’s midday post, borrowing a phrase from the theology of Marvel Comics,
offered Rubik’s mechanical contrivance as a rather absurd “Cosmic Cube.”
A simpler candidate for the “Cube” part of that phrase:

The Eightfold Cube
As noted elsewhere, a simple reflection group* of order 168 acts naturally on this structure.
“Because of their truly fundamental role in mathematics,
even the simplest diagrams concerning finite reflection groups
(or finite mirror systems, or root systems—
the languages are equivalent) have interpretations
of cosmological proportions.”
— Alexandre V. Borovik in “Coxeter Theory: The Cognitive Aspects“
Borovik has a such a diagram—

The planes in Borovik’s figure are those separating the parts of the eightfold cube above.
In Coxeter theory, these are Euclidean hyperplanes. In the eightfold cube, they represent three of seven projective points that are permuted by the above group of order 168.
In light of Borovik’s remarks, the eightfold cube might serve to illustrate the “Cosmic” part of the Marvel Comics phrase.
For some related theological remarks, see Cube Trinity in this journal.
Happy St. Augustine’s Day.
* I.e., one generated by reflections : group actions that fix a hyperplane pointwise. In the eightfold cube, viewed as a vector space of 3 dimensions over the 2-element Galois field, these hyperplanes are certain sets of four subcubes.
Thursday, May 19, 2011
The Aleph, the Lottery, and the Eightfold Way
Three links with a Borges flavor—
Related material
The 236 in yesterday evening's NY lottery may be
viewed as the 236 in March 18's Defining Configurations.
For some background, see Configurations and Squares.
A new illustration for that topic—

This shows a reconcilation of the triples described by Sloane
in Defining Configurations with the square geometric
arrangement described by Coxeter in the Aleph link above.
Note that the 56 from yesterday's midday NY lottery
describes the triples that appear both in the Eightfold Way
link above and also in a possible source for
the eight triples of Sloane's 83 configuration—

The geometric square arrangement discussed in the Aleph link
above appears in a different, but still rather Borgesian, context
in yesterday morning's Minimalist Icon.
Wednesday, May 18, 2011
Minimalist Icon
The source of the mysterious generic
3×3 favicon with one green cell —
![]()
— has been identified.
For minimalists, here is a purer 3×3 matrix favicon—
This may, if one likes, be viewed as the "nothing"
present at the Creation. See Jim Holt on physics.
See also Visualizing GL(2,p), Coxeter and the Aleph, and Ayn Sof.
Tuesday, May 10, 2011
Groups Acting
The LA Times on last weekend's film "Thor"—
"… the film… attempts to bridge director Kenneth Branagh's high-minded Shakespearean intentions with Marvel Entertainment's bottom-line-oriented need to crank out entertainment product."
Those averse to Nordic religion may contemplate a different approach to entertainment (such as Taymor's recent approach to Spider-Man).
A high-minded— if not Shakespearean— non-Nordic approach to groups acting—
"What was wrong? I had taken almost four semesters of algebra in college. I had read every page of Herstein, tried every exercise. Somehow, a message had been lost on me. Groups act . The elements of a group do not have to just sit there, abstract and implacable; they can do things, they can 'produce changes.' In particular, groups arise naturally as the symmetries of a set with structure. And if a group is given abstractly, such as the fundamental group of a simplical complex or a presentation in terms of generators and relators, then it might be a good idea to find something for the group to act on, such as the universal covering space or a graph."
— Thomas W. Tucker, review of Lyndon's Groups and Geometry in The American Mathematical Monthly , Vol. 94, No. 4 (April 1987), pp. 392-394
"Groups act "… For some examples, see
- The 2×2×2 Cube,
- The Diamond 16 Puzzle,
- The Diamond Theorem, and
- Finite Geometry of the Square and Cube.
Related entertainment—
High-minded— Many Dimensions—

Not so high-minded— The Cosmic Cube—

One way of blending high and low—
The high-minded Charles Williams tells a story
in his novel Many Dimensions about a cosmically
significant cube inscribed with the Tetragrammaton—
the name, in Hebrew, of God.
The following figure can be interpreted as
the Hebrew letter Aleph inscribed in a 3×3 square—
The above illustration is from undated software by Ed Pegg Jr.
For mathematical background, see a 1985 note, "Visualizing GL(2,p)."
For entertainment purposes, that note can be generalized from square to cube
(as Pegg does with his "GL(3,3)" software button).
For the Nordic-averse, some background on the Hebrew connection—
Friday, April 22, 2011
Romancing the Hyperspace
For the title, see Palm Sunday.
"There is a pleasantly discursive treatment of
Pontius Pilate's unanswered question 'What is truth?'" — H. S. M. Coxeter, 1987
From this date (April 22) last year—
 Richard J. Trudeau in The Non-Euclidean Revolution , chapter on "Geometry and the Diamond Theory of Truth"– "… Plato and Kant, and most of the philosophers and scientists in the 2200-year interval between them, did share the following general presumptions: (1) Diamonds– informative, certain truths about the world– exist. Presumption (1) is what I referred to earlier as the 'Diamond Theory' of truth. It is far, far older than deductive geometry." Trudeau's book was published in 1987. The non-Euclidean* figures above illustrate concepts from a 1976 monograph, also called "Diamond Theory." Although non-Euclidean,* the theorems of the 1976 "Diamond Theory" are also, in Trudeau's terminology, diamonds. * "Non-Euclidean" here means merely "other than Euclidean." No violation of Euclid's parallel postulate is implied. |
Trudeau comes to reject what he calls the "Diamond Theory" of truth. The trouble with his argument is the phrase "about the world."
Geometry, a part of pure mathematics, is not about the world. See G. H. Hardy, A Mathematician's Apology .
Tuesday, March 29, 2011
Diamond Star
From last night's note on finite geometry—
"The (83, 83) Möbius-Kantor configuration here described by Coxeter is of course part of the larger (94, 123) Hesse configuration. Simply add the center point of the 3×3 Galois affine plane and the four lines (1 horizontal, 1 vertical, 2 diagonal) through the center point." An illustration—

This suggests a search for "diamond+star."
Friday, March 18, 2011
Defining Configurations*
The On-Line Encyclopedia of Integer Sequences has an article titled "Number of combinatorial configurations of type (n_3)," by N.J.A. Sloane and D. Glynn.
From that article:
- DEFINITION: A combinatorial configuration of type (n_3) consists of an (abstract) set of n points together with a set of n triples of points, called lines, such that each point belongs to 3 lines and each line contains 3 points.
- EXAMPLE: The unique (8_3) configuration consists of the triples 125, 148, 167, 236, 278, 347, 358, 456.
The following corrects the word "unique" in the example.

* This post corrects an earlier post, also numbered 14660 and dated 7 PM March 18, 2011, that was in error.
The correction was made at about 11:50 AM on March 20, 2011.
_____________________________________________________________
Update of March 21
The problem here is of course with the definition. Sloane and Glynn failed to include in their definition a condition that is common in other definitions of configurations, even abstract or purely "combinatorial" configurations. See, for instance, Configurations of Points and Lines , by Branko Grunbaum (American Mathematical Society, 2009), p. 17—
In the most general sense we shall consider combinatorial (or abstract) configurations; we shall use the term set-configurations as well. In this setting "points" are interpreted as any symbols (usually letters or integers), and "lines" are families of such symbols; "incidence" means that a "point" is an element of a "line". It follows that combinatorial configurations are special kinds of general incidence structures. Occasionally, in order to simplify and clarify the language, for "points" we shall use the term marks, and for "lines" we shall use blocks. The main property of geometric configurations that is preserved in the generalization to set-configurations (and that characterizes such configurations) is that two marks are incident with at most one block, and two blocks with at most one mark.
Whether or not omitting this "at most one" condition from the definition is aesthetically the best choice, it dramatically changes the number of configurations in the resulting theory, as the above (8_3) examples show.
Update of March 22 (itself updated on March 25)
For further background on configurations, see Dolgachev—

Note that the two examples Dolgachev mentions here, with 16 points and 9 points, are not unrelated to the geometry of 4×4 and 3×3 square arrays. For the Kummer and related 16-point configurations, see section 10.3, "The Three Biplanes of Order 4," in Burkard Polster's A Geometrical Picture Book (Springer, 1998). See also the 4×4 array described by Gordon Royle in an undated web page and in 1980 by Assmus and Sardi. For the Hesse configuration, see (for instance) the passage from Coxeter quoted in Quaternions in an Affine Galois Plane.
Update of March 27
See the above link to the (16,6) 4×4 array and the (16,6) exercises using this array in R.D. Carmichael's classic Introduction to the Theory of Groups of Finite Order (1937), pp. 42-43. For a connection of this sort of 4×4 geometry to the geometry of the diamond theorem, read "The 2-subsets of a 6-set are the points of a PG(3,2)" (a note from 1986) in light of R.W.H.T. Hudson's 1905 classic Kummer's Quartic Surface , pages 8-9, 16-17, 44-45, 76-77, 78-79, and 80.
Monday, February 28, 2011
His Kind of Diamond
In memory of Jane Russell —
H.S.M. Coxeter's classic
Introduction to Geometry (2nd ed.):

Note the resemblance of the central part to
a magical counterpart— the Ojo de Dios
of Mexico's Sierra Madre.
Related material— page 55 of Polly and the Aunt ,
by Mary E. Blatchford.
Saturday, February 26, 2011
The Pope’s Speech
Last night's post was about a talk last year at the annual student symposium of the ACCA (Associated Colleges of the Chicago Area), a group of largely Christian colleges.
The fact that the talk was by a student from Benedictine University suggests a review of the Urbi et Orbi speech by Pope Benedict XVI on Christmas 2010.
“The Word became flesh”. The light of this truth is revealed to those who receive it in faith, for it is a mystery of love. Only those who are open to love are enveloped in the light of Christmas. So it was on that night in Bethlehem, and so it is today. The Incarnation of the Son of God is an event which occurred within history, while at the same time transcending history. In the night of the world a new light was kindled, one which lets itself be seen by the simple eyes of faith, by the meek and humble hearts of those who await the Saviour. If the truth were a mere mathematical formula, in some sense it would impose itself by its own power. But if Truth is Love, it calls for faith, for the “yes” of our hearts.
And what do our hearts, in effect, seek, if not a Truth which is also Love? Children seek it with their questions, so disarming and stimulating; young people seek it in their eagerness to discover the deepest meaning of their life; adults seek it in order to guide and sustain their commitments in the family and the workplace; the elderly seek it in order to grant completion to their earthly existence.
The above excerpt from the Pope's speech may be regarded as part of a continuing commentary on the following remark—
There is a pleasantly discursive treatment of Pontius Pilate's unanswered question "What is truth?" — H. S. M. Coxeter, 1987
Friday, January 7, 2011
Ayn Sof
(A continuation of this morning's Coxeter and the Aleph)
"You've got to pick up every stitch… Must be the season of the witch."
— Donovan song at the end of Nicole Kidman's "To Die For"
| Mathematics and Narrative, Illustrated | |

|
 Narrative |
"As is well known, the Aleph is the first letter of the Hebrew alphabet.
Its use for the strange sphere in my story may not be accidental.
For the Kabbala, the letter stands for the En Soph ,
the pure and boundless godhead; it is also said that it takes
the shape of a man pointing to both heaven and earth, in order to show
that the lower world is the map and mirror of the higher; for Cantor's
Mengenlehre , it is the symbol of transfinite numbers,
of which any part is as great as the whole."
— Borges, "The Aleph"
From WorldLingo.com —
|
"Infinite Jest… now stands as the principal contender
for what serious literature can aspire to
in the late twentieth and early twenty-first centuries."
— All Things Shining, a work of pop philosophy published January 4th
"You're gonna need a bigger boat." — Roy Scheider in "Jaws"
"We're gonna need more holy water." — "Season of the Witch," a film opening tonight
See also, with respect to David Foster Wallace, infinity, nihilism,
and the above reading of "Ayn Sof" as "nothingness,"
the quotations compiled as "Is Nothing Sacred?"
Tuesday, November 23, 2010
Back to the Saddle
Recent posts (Church Logic and Church Narrative) have discussed finite geometry as a type of non-Euclidean geometry.
For those who prefer non-finite geometry, here are some observations.

"A characteristic property of hyperbolic geometry
is that the angles of a triangle add to less
than a straight angle (half circle)." — Wikipedia

From To Ride Pegasus, by Anne McCaffrey, 1973:
“Mary-Molly luv, it’s going to be accomplished in steps, this establishment of the Talented in the scheme of things. Not society, mind you, for we’re the original nonconformists…. and Society will never permit us to integrate. That’s okay!” He consigned Society to insignificance with a flick of his fingers. “The Talented form their own society and that’s as it should be: birds of a feather. No, not birds. Winged horses! Ha! Yes, indeed. Pegasus… the poetic winged horse of flights of fancy. A bloody good symbol for us. You’d see a lot from the back of a winged horse…”
“Yes, an airplane has blind spots. Where would you put a saddle?” Molly had her practical side.
On the practical side:

The above chapel is from a Princeton Weekly Bulletin story of October 6th, 2008.
Related material: This journal on that date.
Saturday, November 20, 2010
Search
An Epic Search for Truth
— Subtitle of Logicomix , a work reviewed in the December 2010 Notices of the American Mathematical Society (see previous post).
Some future historian of mathematics may contrast the lurid cover of the December 2010 Notices
Excerpts from Logicomix
with the 1979 cover found in a somewhat less epic search —

Larger view of Google snippet —

For some purely mathematical background, see Finite Geometry of the Square and Cube.
For some background related to searches for truth, see "Coxeter + Trudeau" in this journal.
Tuesday, October 19, 2010
Savage Logic continued…
CHAPTER V
"This is an account of the discrete groups generated by reflections…."
— Regular Polytopes , by H.S.M. Coxeter (unabridged and corrected 1973 Dover reprint of the 1963 Macmillan second edition)
"In this article, we begin a theory linking hyperplane arrangements and invariant forms for reflection groups over arbitrary fields…. Let V be an n-dimensional vector space over a field F, and let G ≤ Gln (F) be a finite group…. An element of finite order in Gl(V ) is a reflection if its fixed point space in V is a hyperplane, called the reflecting hyperplane. There are two types of reflections: the diagonalizable reflections in Gl(V ) have a single nonidentity eigenvalue which is a root of unity; the nondiagonalizable reflections in Gl(V ) are called transvections and have determinant 1 (note that they can only occur if the characteristic of F is positive)…. A reflection group is a finite group G generated by reflections."
— Julia Hartmann and Anne V. Shepler, "Reflection Groups and Differential Forms," Mathematical Research Letters , Vol. 14, No. 6 (Nov. 2007), pp. 955-971
"… the class of reflections is larger in some sense over an arbitrary field than over a characteristic zero field. The reflections in Gl(V ) not only include diagonalizable reflections (with a single nonidentity eigenvalue), but also transvections, reflections with determinant 1 which can not be diagonalized. The transvections in Gl(V ) prevent one from developing a theory of reflection groups mirroring that for Coxeter groups or complex reflection groups."
— Julia Hartmann and Anne V. Shepler, "Jacobians of Reflection Groups," Transactions of the American Mathematical Society , Vol. 360, No. 1 (2008), pp. 123-133 (Pdf available at CiteSeer.)
See also A Simple Reflection Group of Order 168 and this morning's Savage Logic.
Saturday, August 7, 2010
The Matrix Reloaded
For aficionados of mathematics and narrative —
Illustration from
"The Galois Quaternion— A Story"
This resembles an attempt by Coxeter in 1950 to represent
a Galois geometry in the Euclidean plane—
The quaternion illustration above shows a more natural way to picture this geometry—
not with dots representing points in the Euclidean plane, but rather with unit squares
representing points in a finite Galois affine plane. The use of unit squares to
represent points in Galois space allows, in at least some cases, the actions
of finite groups to be represented more naturally than in Euclidean space.
See Galois Geometry, Geometry Simplified, and
Finite Geometry of the Square and Cube.
Monday, July 12, 2010
Eyes on the Prize
Google Logo July 11, 2010—

"Oog" is Dutch (and Afrikaans) for "eye."
Strong Emergence Illustrated
(May 23, 2007 — Figures from Coxeter)—
The 2007 "strong emergence" post compares the
center figure to an "Ojo de Dios."
Thursday, July 8, 2010
Toronto vs. Rome
or: Catullus vs. Ovid
(Today's previous post, "Coxeter vs. Fano,"
might also have been titled "Toronto vs. Rome.")
ut te postremo donarem munere mortis
Explicatio
Image by Christopher Thomas at Wikipedia —
Unfolding of a hypercube and of a cube —


The metaphor for metamorphosis no keys unlock.
— Steven H. Cullinane, "Endgame"
The current New Yorker has a translation of
the above line of Catullus by poet Anne Carson.
According to poets.org, Carson "attended St. Michael's College
at the University of Toronto and, despite leaving twice,
received her B.A. in 1974, her M.A. in 1975 and her Ph.D. in 1981."
Carson's translation is given in a review of her new book Nox.
The title, "The Unfolding," of the current review echoes an earlier
New Yorker piece on another poet, Madeleine L'Engle—
Cynthia Zarin in The New Yorker, issue dated April 12, 2004–
“Time, for L’Engle, is accordion-pleated. She elaborated,
‘When you bring a sheet off the line, you can’t handle it
until it’s folded, and in a sense, I think, the universe can’t
exist until it’s folded– or it’s a story without a book.’”
(See also the "harrow up" + Hamlet link in yesterday's 6:29 AM post.)
Sunday, June 20, 2010
Sunday School
|
Limited— Good |
Unlimited— Bad
|
Jamie James in The Music of the Spheres—
"The Pythagorean philosophy, like Zoroastrianism, Taoism, and every early system of higher thought, is based upon the concept of dualism. Pythagoras constructed a table of opposites from which he was able to derive every concept needed for a philosophy of the phenomenal world. As reconstructed by Aristotle in his Metaphysics, the table contains ten dualities (ten being a particularly important number in the Pythagorean system, as we shall see):
| Limited Odd One Right Male Rest Straight Light Good Square |
Unlimited Even Many Left Female Motion Curved Dark Bad Oblong |
Of these dualities, the first is the most important; all the others may be seen as different aspects of this fundamental dichotomy. To establish a rational and consistent relationship between the limited (man, finite time, and so forth) and the unlimited (the cosmos, eternity, etc.) is not only the aim of Pythagoras's system but the central aim of all Western philosophy."
Monday, May 10, 2010
Requiem for Georgia Brown
Paul Robeson in
"King Solomon's Mines," 1937—
The image above is an illustration from
"Romancing the Hyperspace," May 4, 2010.
This illustration, along with Georgia Brown's
song from "Cabin in the Sky"—
"There's honey in the honeycomb"—
suggests the following picture.
"What might have been and what has been
Point to one end, which is always present."
— Four Quartets
Saturday, April 10, 2010
Geometry for Generations
"Let G be a finite, primitive subgroup of
— William M. Kantor, "Generation of Linear Groups," pp. 497-509 in The Geometric Vein: The Coxeter Festschrift, published by Springer, 1981
This quote was added today to "A Simple Reflection Group of Order 168."
Sunday, April 4, 2010
URBI ET ORBI
URBI
(Toronto)–
Click on image for some background.
ORBI
(Globe and Mail)–
See also Baaad Blake and
Fearful Symmetry.
Tuesday, March 16, 2010
Variations on a Theme
Today's previous entry was "Gameplayers of the Academy."
David Corfield in the March 2010
European Mathematical Society newsletter—
"Staying on the theme of games, the mathematician
Alexandre Borovik* once told me he thinks of mathematics
as a Massively-Multiplayer Online Role-Playing Game. If
so, it would show up very clearly the difference between
internal and external viewpoints. Inside the game people
are asking each other whether they were right about
something they encountered in it– 'When you entered
the dungeon did you see that dragon in the fireplace or
did I imagine it?' But someone observing them from the
outside wants to shout: 'You’re not dealing with anything
real. You’ve just got a silly virtual reality helmet on.' External
nominalists say the same thing, if more politely, to
mathematical practitioners. But in an important way the
analogy breaks down. Even if the players interact with
the game to change its functioning in unforeseen ways,
there were the original programmers who set the bounds
for what is possible by the choices they made. When they
release the next version of the game they will have made
changes to allow new things to happen. In the case of
mathematics, it’s the players themselves who make these
choices. There’s no further layer outside.
What can we do then instead to pin down internal reality?"
*See previous references to Borovik in this journal.
Related material:
The Diamond Theory vs. the Story Theory of Truth,
Infantilizing the Audience, and
It's Still the Same Old Story…God of War III
Sunday, February 21, 2010
Reflections, continued
"The eye you see him with is the same
eye with which he sees you."
– Father Egan on page 333
of Robert Stone's A Flag for Sunrise
(Knopf hardcover, 1981)
Part I– Bounded in a Nutshell

Ian McKellen at a mental hospital's diamond-shaped window in "Neverwas"
Part II– The Royal Castle
Ian McKellen at his royal castle's diamond-shaped window in "Neverwas"
Part III– King of Infinite Space

H.S.M. Coxeter crowns himself "King of Infinite Space"
Related material:
See Coxeter in this journal.
Reflections
From the Wikipedia article "Reflection Group" that I created on Aug. 10, 2005— as revised on Nov. 25, 2009—
|
Historically, (Coxeter 1934) proved that every reflection group [Euclidean, by the current Wikipedia definition] is a Coxeter group (i.e., has a presentation where all relations are of the form ri2 or (rirj)k), and indeed this paper introduced the notion of a Coxeter group, while (Coxeter 1935) proved that every finite Coxeter group had a representation as a reflection group [again, Euclidean], and classified finite Coxeter groups. Finite fields
When working over finite fields, one defines a "reflection" as a map that fixes a hyperplane (otherwise for example there would be no reflections in characteristic 2, as −1=1 so reflections are the identity). Geometrically, this amounts to including shears in a hyperplane. Reflection groups over finite fields of characteristic not 2 were classified in (Zalesskiĭ & Serežkin 1981). |
Related material:
"A Simple Reflection Group of Order 168," by Steven H. Cullinane, and
by Ascher Wagner, U. of Birmingham, received 27 July 1977
| Journal | Geometriae Dedicata |
| Publisher | Springer Netherlands |
| Issue | Volume 9, Number 2 / June, 1980 |

[A primitive permuation group preserves
no nontrivial partition of the set it acts upon.]
Clearly the eightfold cube is a counterexample.
Thursday, February 18, 2010
Theories: An Outline
Truth, Geometry, Algebra
The following notes are related to A Simple Reflection Group of Order 168.
1. According to H.S.M. Coxeter and Richard J. Trudeau
“There is a pleasantly discursive treatment of Pontius Pilate’s unanswered question ‘What is truth?’.”
— Coxeter, 1987, introduction to Trudeau’s The Non-Euclidean Revolution
1.1 Trudeau’s Diamond Theory of Truth
1.2 Trudeau’s Story Theory of Truth
2. According to Alexandre Borovik and Steven H. Cullinane
2.1 Coxeter Theory according to Borovik
2.1.1 The Geometry–
Mirror Systems in Coxeter Theory
2.1.2 The Algebra–
Coxeter Languages in Coxeter Theory
2.2 Diamond Theory according to Cullinane
2.2.1 The Geometry–
Examples: Eightfold Cube and Solomon’s Cube
2.2.2 The Algebra–
Examples: Cullinane and (rather indirectly related) Gerhard Grams
Summary of the story thus far:
Diamond theory and Coxeter theory are to some extent analogous– both deal with reflection groups and both have a visual (i.e., geometric) side and a verbal (i.e., algebraic) side. Coxeter theory is of course highly developed on both sides. Diamond theory is, on the geometric side, currently restricted to examples in at most three Euclidean (and six binary) dimensions. On the algebraic side, it is woefully underdeveloped. For material related to the algebraic side, search the Web for generators+relations+”characteristic two” (or “2“) and for generators+relations+”GF(2)”. (This last search is the source of the Grams reference in 2.2.2 above.)
Tuesday, February 16, 2010
Mysteries of Faith
From today's NY Times—

Obituaries for mystery authors
Ralph McInerny and Dick Francis
From the date (Jan. 29) of McInerny's death–
"…although a work of art 'is formed around something missing,' this 'void is its vanishing point, not its essence.'"
– Harvard University Press on Persons and Things (Walpurgisnacht, 2008), by Barbara Johnson
From the date (Feb. 14) of Francis's death–

The EIghtfold Cube
The "something missing" in the above figure is an eighth cube, hidden behind the others pictured.
This eighth cube is not, as Johnson would have it, a void and "vanishing point," but is instead the "still point" of T.S. Eliot. (See the epigraph to the chapter on automorphism groups in Parallelisms of Complete Designs, by Peter J. Cameron. See also related material in this journal.) The automorphism group here is of course the order-168 simple group of Felix Christian Klein.
For a connection to horses, see
a March 31, 2004, post
commemorating the birth of Descartes
and the death of Coxeter–
Putting Descartes Before Dehors


For a more Protestant meditation,
see The Cross of Descartes—

"I've been the front end of a horse
and the rear end. The front end is better."
— Old vaudeville joke
For further details, click on
the image below–
Notre Dame Philosophical Reviews
Sunday, February 14, 2010
Sunday School
"Simplify, simplify." — Henry David Thoreau
"Because of their truly fundamental role in mathematics, even the simplest diagrams concerning finite reflection groups (or finite mirror systems, or root systems– the languages are equivalent) have interpretations of cosmological proportions."
— Alexandre Borovik, 2010 (See previous entry.)
Exercise: Discuss Borovik's remark
that "the languages are equivalent"
in light of the web page

A Simple Reflection Group
of Order 168.
Background:
Theorems 15.1 and 15.2 of Borovik's book (1st ed. Nov. 10, 2009)
Mirrors and Reflections: The Geometry of Finite Reflection Groups—
15.1 (p. 114): Every finite reflection group is a Coxeter group.
15.2 (p. 114): Every finite Coxeter group is isomorphic to a finite reflection group.
Consider in this context the above simple reflection group of order 168.
(Recall that "…there is only one simple Coxeter group (up to isomorphism); it has order 2…" —A.M. Cohen.)
Sunday, September 27, 2009
Sunday September 27, 2009
Discursive Treatment
Unitarian Universalist Origins: Our Historic Faith—
“In sixteenth-century Transylvania, Unitarian congregations were established for the first time in history.”
Gravity’s Rainbow–
“For every kind of vampire, there is a kind of cross.”
Unitarian minister Richard Trudeau—
“… I called the belief that
(1) Diamonds– informative, certain truths about the world– exist
the ‘Diamond Theory’ of truth. I said that for 2200 years the strongest evidence for the Diamond Theory was the widespread perception that
(2) The theorems of Euclidean geometry are diamonds….
As the news about non-Euclidean geometry spread– first among mathematicians, then among scientists and philosophers– the Diamond Theory began a long decline that continues today.
Factors outside mathematics have contributed to this decline. Euclidean geometry had never been the Diamond Theory’s only ally. In the eighteenth century other fields had seemed to possess diamonds, too; when many of these turned out to be man-made, the Diamond Theory was undercut. And unlike earlier periods in history, when intellectual shocks came only occasionally, received truths have, since the eighteenth century, been found wanting at a dizzying rate, creating an impression that perhaps no knowledge is stable.
Other factors notwithstanding, non-Euclidean geometry remains, I think, for those who have heard of it, the single most powerful argument against the Diamond Theory*– first, because it overthrows what had always been the strongest argument in favor of the Diamond Theory, the objective truth of Euclidean geometry; and second, because it does so not by showing Euclidean geometry to be false, but by showing it to be merely uncertain.” —The Non-Euclidean Revolution, p. 255
H. S. M. Coxeter, 1987, introduction to Trudeau’s book—
“There is a pleasantly discursive treatment of Pontius Pilate’s unanswered question ‘What is truth?’.”
As noted here on Oct. 8, 2008 (A Yom Kippur Meditation), Coxeter was aware in 1987 of a more technical use of the phrase “diamond theory” that is closely related to…
of cross:

Friday, April 10, 2009
Friday April 10, 2009
Pilate Goes
to Kindergarten
“There is a pleasantly discursive
treatment of Pontius Pilate’s
unanswered question
‘What is truth?’.”
— H. S. M. Coxeter, 1987,
introduction to Trudeau’s
remarks on the “Story Theory“
of truth as opposed to the
“Diamond Theory” of truth in
The Non-Euclidean Revolution
Consider the following question in a paper cited by V. S. Varadarajan:
E. G. Beltrametti, “Can a finite geometry describe physical space-time?” Universita degli studi di Perugia, Atti del convegno di geometria combinatoria e sue applicazioni, Perugia 1971, 57–62.
Simplifying:
“Can a finite geometry describe physical space?”
Simplifying further:
“Yes. Vide ‘The Eightfold Cube.'”

Friday, January 30, 2009
Friday January 30, 2009
| This journal on October 8, 2008, at noon: “There is a pleasantly discursive treatment of Pontius Pilate’s unanswered question ‘What is truth?'” Trudeau’s 1987 book uses the phrase “diamond theory” to denote the philosophical theory, common since Plato and Euclid, that there exist truths (which Trudeau calls “diamonds”) that are certain and eternal– for instance, the truth in Euclidean geometry that the sum of a triangle’s angles is 180 degrees. Insidehighered.com onthe same day, October 8, 2008, at 12:45 PM EDT “Future readers may consider Updike our era’s Mozart; Mozart was once written off as a too-prolific composer of ‘charming nothings,’ and some speak of Updike that way.” — Comment by BPJ |
what day is not both?”
— John Updike
Updike died on January 27.
On the same date,
Mozart was born.
Requiem
| Mr. Best entered, tall, young, mild, light. He bore in his hand with grace a notebook, new, large, clean, bright. — James Joyce, Ulysses, |
Saturday, November 8, 2008
Saturday November 8, 2008
Cartoon Graveyard “That corpse you planted
last year in your garden,
Has it begun to sprout?
Will it bloom this year?
Or has the sudden frost
disturbed its bed?”
— T. S. Eliot, “The Waste Land“
“In the Roman Catholic tradition, the term ‘Body of Christ’ refers not only to the body of Christ in the spiritual realm, but also to two distinct though related things: the Church and the reality of the transubstantiated bread of the Eucharist….
According to the Catechism of the Catholic Church, ‘the comparison of the Church with the body casts light on the intimate bond between Christ and his Church. Not only is she gathered around him; she is united in him, in his body….’
….To distinguish the Body of Christ in this sense from his physical body, the term ‘Mystical Body of Christ’ is often used. This term was used as the first words, and so as the title, of the encyclical Mystici Corporis Christi of Pope Pius XII.”
Pope Pius XII:
“83. The Sacrament of the Eucharist is itself a striking and wonderful figure of the unity of the Church, if we consider how in the bread to be consecrated many grains go to form one whole, and that in it the very Author of supernatural grace is given to us, so that through Him we may receive the spirit of charity in which we are bidden to live now no longer our own life but the life of Christ, and to love the Redeemer Himself in all the members of His social Body.”
Log24 on this date in 2002:
Religious Symbolism
at Princeton
as well as
and a
“striking and wonderful figure”
from this morning’s newspaper–

Wednesday, October 8, 2008
Wednesday October 8, 2008
Serious Numbers
A Yom Kippur
Meditation
"When times are mysterious
Serious numbers
Will always be heard."
— Paul Simon,
"When Numbers Get Serious"
"There is a pleasantly discursive treatment of Pontius Pilate's unanswered question 'What is truth?'"
— H. S. M. Coxeter, introduction to Richard J. Trudeau's remarks on the "story theory" of truth as opposed to the "diamond theory" of truth in The Non-Euclidean Revolution
Trudeau's 1987 book uses the phrase "diamond theory" to denote the philosophical theory, common since Plato and Euclid, that there exist truths (which Trudeau calls "diamonds") that are certain and eternal– for instance, the truth in Euclidean geometry that the sum of a triangle's angles is 180 degrees. As the excerpt below shows, Trudeau prefers what he calls the "story theory" of truth–
"There are no diamonds. People make up stories about what they experience. Stories that catch on are called 'true.'"
(By the way, the phrase "diamond theory" was used earlier, in 1976, as the title of a monograph on geometry of which Coxeter was aware.)

Excerpt from
The Non-Euclidean Revolution
What does this have to do with numbers?
Pilate's skeptical tone suggests he may have shared a certain confusion about geometric truth with thinkers like Trudeau and the slave boy in Plato's Meno. Truth in a different part of mathematics– elementary arithmetic– is perhaps more easily understood, although even there, the existence of what might be called "non-Euclidean number theory"– i.e., arithmetic over finite fields, in which 1+1 can equal zero– might prove baffling to thinkers like Trudeau.
Trudeau's book exhibits, though it does not discuss, a less confusing use of numbers– to mark the location of pages. For some philosophical background on this version of numerical truth that may be of interest to devotees of the Semitic religions on this evening's High Holiday, see Zen and Language Games.
For uses of numbers that are more confusing, see– for instance– the new website The Daily Beast and the old website Story Theory and the Number of the Beast.
Friday, July 4, 2008
Friday July 4, 2008
"I need a photo-opportunity,
I want a shot at redemption.
Don't want to end up a cartoon
In a cartoon graveyard."
— Paul Simon
From Log24 on June 27, 2008,
the day that comic-book artist
Michael Turner died at 37 —
Van Gogh (by Ed Arno) in
The Paradise of Childhood
(by Edward Wiebé):
For Turner's photo-opportunity,
click on Lara.
Sunday, June 1, 2008
Sunday June 1, 2008
Cartoon Graveyard
The conclusion of yesterday’s commentary on the May 30-31 Pennsylvania Lottery numbers:
Thomas Pynchon, Gravity’s Rainbow:
“The fear balloons again inside his brain. It will not be kept down with a simple Fuck You…. A smell, a forbidden room, at the bottom edge of his memory. He can’t see it, can’t make it out. Doesn’t want to. It is allied with the Worst Thing.
He knows what the smell has to be: though according to these papers it would have been too early for it, though he has never come across any of the stuff among the daytime coordinates of his life, still, down here, back here in the warm dark, among early shapes where the clocks and calendars don’t mean too much, he knows that’s what haunting him now will prove to be the smell of Imipolex G.
Then there’s this recent dream he is afraid of having again. He was in his old room, back home. A summer afternoon of lilacs and bees and
286”
What are we to make of this enigmatic 286? (No fair peeking at page 287.)
One possible meaning, given The Archivist‘s claim that “existence is infinitely cross-referenced”–
Page 286 of Ernest G. Schachtel, Metamorphosis: On the Conflict of Human Development and the Psychology of Creativity (first published in 1959), Hillsdale NJ and London, The Analytic Press, 2001 (chapter– “On Memory and Childhood Amnesia”):
“Both Freud and Proust speak of the autobiographical [my italics] memory, and it is only with regard to this memory that the striking phenomenon of childhood amnesia and the less obvious difficulty of recovering any past experience may be observed.”
The concluding “summer afternoon of lilacs and bees” suggests that 286 may also be a chance allusion to the golden afternoon of Disney’s Alice in Wonderland. (Cf. St. Sarah’s Day, 2008)
Some may find the Disney afternoon charming; others may see it as yet another of Paul Simon’s dreaded cartoon graveyards.
More tastefully, there is poem 286 in the 1919 Oxford Book of English Verse– “Love.”
For a midrash on this poem, see Simone Weil, who became acquainted with the poem by chance:
“I always prefer saying chance rather than Providence.”
— Simone Weil, letter of about May 15, 1942
Weil’s brother André might prefer Providence (source of the Bulletin of the American Mathematical Society.)
 (Photo from Providence)
(Photo from Providence)
White, Geometric, and Eternal—
For more on the mathematical significance of this figure, see (for instance) Happy Birthday, Hassler Whitney, and Combinatorics of Coxeter Groups, by Anders Björner and Francesco Brenti, Graduate Texts in Mathematics, vol. 231, Springer, New York, 2005.
This book is reviewed in the current issue (July 2008) of the above-mentioned Providence Bulletin.
The review in the Bulletin discusses reflection groups in continuous spaces.
the phrase “as a little child.”
Sunday, May 25, 2008
Sunday May 25, 2008
Epigraph to
“Deploying the Glass Bead Game, Part II,”
by Robert de Marrais:
“For a complete logical argument,”
Arthur began
with admirable solemnity,
“we need two prim Misses –”
“Of course!” she interrupted.
“I remember that word now.
And they produce — ?”
“A Delusion,” said Arthur.
— Lewis Carroll,
Sylvie and Bruno
Erin O’Connor’s weblog “Critical Mass” on May 24:
Roger Rosenblatt’s Beet [Ecco hardcover, Jan. 29, 2008] is the latest addition to the noble sub-genre of campus fiction….
Curricular questions and the behavior of committees are at once dry as dust subjects and areas ripe for sarcastic send-up– not least because, as dull as they are, they are really both quite vital to the credibility and viability of higher education.
Here’s an excerpt from the first meeting, in which committee members propose their personal plans for a new, improved curriculum:
“… Once the students really got into playing with toy soldiers, they would understand history with hands-on excitement.”
To demonstrate his idea, he’d brought along a shoe box full of toy doughboys and grenadiers, and was about to reenact the Battle of Verdun on the committee table when Heilbrun stayed his hand. “We get it,” he said.
“That’s quite interesting, Molton,” said Booth [a chemist]. “But is it rigorous enough?”
At the mention of the word, everyone, save Peace, sat up straight.
“Rigor is so important,” said Kettlegorf.
“We must have rigor,” said Booth.
“You may be sure,” said the offended Kramer. “I never would propose anything lacking rigor.”
Smythe inhaled and looked at the ceiling. “I think I may have something of interest,” he said, as if he were at a poker game and was about to disclose a royal flush. “My proposal is called ‘Icons of Taste.’ It would consist of a galaxy of courses affixed to several departments consisting of lectures on examples of music, art, architecture, literature, and other cultural areas a student needed to indicate that he or she was sophisticated.”
“Why would a student want to do that?” asked Booth.
“Perhaps sophistication is not a problem for chemists,” said Smythe. Lipman tittered.
“What’s the subject matter?” asked Heilbrun. “Would it have rigor?”
“Of course it would have rigor. Yet it would also attract those additional students Bollovate is talking about.” Smythe inhaled again. “The material would be carefully selected,” he said. “One would need to pick out cultural icons the students were likely to bring up in conversation for the rest of their lives, so that when they spoke, others would recognize their taste as being exquisite yet eclectic and unpredictable.”
“You mean Rembrandt?” said Kramer.
Smythe smiled with weary contempt. “No, I do not mean Rembrandt. I don’t mean Beethoven or Shakespeare, either, unless something iconic has emerged about them to justify their more general appeal.”
“You mean, if they appeared on posters,” said Lipman.
“That’s it, precisely.”
Lipman blushed with pride.
“The subject matter would be fairly easy to amass,” Smythe said. “We could all make up a list off the top of our heads. Einstein–who does have a poster.” He nodded to the ecstatic Lipman. “Auden, for the same reason. Students would need to be able to quote ‘September 1939[ or at least the last lines. And it would be good to teach ‘Musee des Beaux Arts’ as well, which is off the beaten path, but not garishly. Mahler certainly. But Cole Porter too. And Sondheim, I think. Goya. Warhol, it goes without saying, Stephen Hawking, Kurosawa, Bergman, Bette Davis. They’d have to come up with some lines from Dark Victory, or better still, Jezebel. La Dolce Vita. Casablanca. King of Hearts. And Orson, naturally. Citizen Kane, I suppose, though personally I prefer F for Fake.”
“Judy!” cried Heilbrun.
“Yes, Judy too. But not ‘Over the Rainbow.’ It would be more impressive for them to do ‘The Trolley Song,’ don’t you think?” Kettlegorf hummed the intro.
“Guernica,” said Kramer. “Robert
Capa.” “Edward R. Murrow,” said Lipman.
“No! Don’t be ridiculous!” said Smythe, ending Lipman’s brief foray into the world of respectable thought.
“Marilyn Monroe!” said Kettlegorf.
“Absolutely!” said Smythe, clapping to indicate his approval.
“And the Brooklyn Bridge,” said Booth, catching on. “And the Chrysler Building.”
“Maybe,” said Smythe. “But I wonder if the Chrysler Building isn’t becoming something of a cliche.”
Peace had had enough. “And you want students to nail this stuff so they’ll do well at cocktail parties?”
Smythe sniffed criticism, always a tetchy moment for him. “You make it sound so superficial,” he said.
Prim Miss 2:
Siri Hustvedt speaks at Adelaide Writers’ Week– a story dated March 24,
“I have come to think of my books as echo chambers or halls of mirrors in which themes, ideas, associations continually reflect and reverberate inside a text. There is always point and counterpoint, to use a musical illustration. There is always repetition with difference.”
A Delusion:
Exercise — Identify in the following article the sentence that one might (by unfairly taking it out of context) argue is a delusion.
(Hint: See Reflection Groups in Finite Geometry.)

Why Borovik’s Figure 4
is included above:
No Royal Roads.
For more on Prim Miss 2
and deploying
the Glass Bead Game,
see the previous entry.
 And now, perhaps, his brother Cornell Capa, who died Friday.
And now, perhaps, his brother Cornell Capa, who died Friday.† Related material: Log24 on March 24– Death and the Apple Tree— with an excerpt from George MacDonald, and an essay by David L. Neuhouser mentioning the influence of MacDonald on Lewis Carroll– Lewis Carroll: Author, Mathematician, and Christian (pdf).
Sunday, May 18, 2008
Sunday May 18, 2008
From the Grave
in yesterday's New York Times:
"From the grave, Albert Einstein
poured gasoline on the culture wars
between science and religion this week…."
An announcement of a
colloquium at Princeton:
Above: a cartoon,
"Coxeter exhuming Geometry,"
with the latter's tombstone inscribed
"GEOMETRY
600 B.C. —
1900 A.D.
R.I.P."

The above is from
The Paradise of Childhood,
a work first published in 1869.
"I need a photo-opportunity,
I want a shot at redemption.
Don't want to end up a cartoon
In a cartoon graveyard."
— Paul Simon

Albert Einstein,
1879-1955:
"It is quite clear to me that the religious paradise of youth, which was thus lost, was a first attempt to free myself from the chains of the 'merely-personal,' from an existence which is dominated by wishes, hopes and primitive feelings. Out yonder there was this huge world, which exists independently of us human beings and which stands before us like a great, eternal riddle, at least partially accessible to our inspection and thinking. The contemplation of this world beckoned like a liberation…."
— Autobiographical Notes, 1949
Related material:
A commentary on Tom Wolfe's
"Sorry, but Your Soul Just Died"–
"The Neural Buddhists," by David Brooks,
in the May 13 New York Times:
"The mind seems to have
the ability to transcend itself
and merge with a larger
presence that feels more real."
A New Yorker commentary on
a new translation of the Psalms:
"Suddenly, in a world without
Heaven, Hell, the soul, and
eternal salvation or redemption,
the theological stakes seem
more local and temporal:
'So teach us to number our days.'"
and a May 13 Log24 commentary
on Thomas Wolfe's
"Only the Dead Know Brooklyn"–
"… all good things — trout as well as
eternal salvation — come by grace
and grace comes by art
and art does not come easy."
"Art isn't easy."
— Stephen Sondheim,
quoted in
Solomon's Cube.
For further religious remarks,
consult Indiana Jones and the
Kingdom of the Crystal Skull
and The Librarian:
Return to King Solomon's Mines.
Thursday, March 27, 2008
Thursday March 27, 2008
Back to the Garden
Film star Richard Widmark
died on Monday, March 24.
From Log24 on that date:
"Hanging from the highest limb
of the apple tree are
the three God's Eyes…"
Related material:
The Beauty Test, 5/23/07–
H.S.M. Coxeter's classic
Introduction to Geometry (2nd ed.):

Note the resemblance of
the central part to
a magical counterpart–
the Ojo de Dios
of Mexico's Sierra Madre.
From a Richard Widmark film festival:
GARDEN OF EVIL
Henry Hathaway, 1954
"A severely underrated Scope western, shot in breathtaking mountain locations near Cuernavaca. Widmark, Gary Cooper and Cameron Mitchell are a trio of fortune hunters stranded in Mexico, when they are approached by Susan Hayward to rescue her husband (Hugh Marlowe) from a caved-in gold mine in Indian country. When they arrive at the 'Garden of Evil,' they must first battle with one another before they have to stave off their bloodthirsty Indian attackers. Widmark gives a tough, moving performance as Fiske, the one who sacrifices himself to save his friends. 'Every day it goes, and somebody goes with it,' he says as he watches the setting sun. 'Today it's me.' This was one of the best of Hollywood veteran Henry Hathaway's later films. With a brilliant score by Bernard Herrmann."
See also
the apple-tree
entries from Monday
(the date of Widmark's death)
and Tuesday, as well as
today's previous entry and
previous Log24
entries on Cuernavaca.
Thursday, March 6, 2008
Thursday March 6, 2008
This note is prompted by the March 4 death of Richard D. Anderson, writer on geometry, President (1981-82) of the Mathematical Association of America (MAA), and member of the MAA's Icosahedron Society.
"The historical road
from the Platonic solids
to the finite simple groups
is well known."
— Steven H. Cullinane,
November 2000,
Symmetry from Plato to
the Four-Color Conjecture
"By far the most important structure in design theory is the Steiner system S(5, 8, 24)."
This Steiner system is closely connected to M24 and to the extended binary Golay code. Brouwer gives an elegant construction of that code (and therefore of M24):
"Let N be the adjacency matrix of the icosahedron (points: 12 vertices, adjacent: joined by an edge). Then the rows of the 12×24 matrix
— Op. cit., p. 719
Finite Geometry of
the Square and Cube
and
Jewel in the Crown
"There is a pleasantly discursive
treatment of Pontius Pilate's
unanswered question
'What is truth?'"
— H. S. M. Coxeter, 1987,
introduction to Trudeau's
"story theory" of truth
Those who prefer stories to truth
may consult the Log24 entries
of March 1, 2, 3, 4, and 5.
They may also consult
the poet Rubén Darío:
… Todo lo sé por el lucero puro
que brilla en la diadema de la Muerte.
* For a road out of this wasteland, back to geometry, see The Kaleidoscope Puzzle and Reflection Groups in Finite Geometry.
Saturday, January 26, 2008
Saturday January 26, 2008
Those who have followed the links here recently may appreciate a short story told by yesterday’s lottery numbers in Pennsylvania: mid-day 096, evening 513.
The “96” may be regarded as a reference to the age at death of geometer H.S.M. Coxeter (see yesterday morning’s links). The “513” may be regarded as a reference to the time of yesterday afternoon’s entry, 5:01, plus the twelve minutes discussed in that entry by presidential aide Richard Darman, who died yesterday.
These references may seem less fanciful in the light of other recent Log24 material: a verse quoted here on Jan. 18—
que brilla en la diadema de la Muerte.
— Rubén Darío,
born January 18, 1867
— and a link on Jan. 19 to the following:
and the Wardrobe:
|
“But what does it all mean?” asked Susan when they were somewhat calmer. “It means,” said Aslan, “that though the Witch knew the Deep Magic, there is a magic deeper still which she did not know. Her knowledge goes back only to the dawn of Time. But if she could have looked a little further back, into the stillness and the darkness before Time dawned, she would have read there a different incantation. She would have known that when a willing victim who had committed no treachery was killed in a traitor’s stead, the Table would crack and Death itself would start working backward.” |
Friday, January 25, 2008
Monday, December 24, 2007
Monday December 24, 2007
From Saturday's entry
(Log24, Dec. 22, 2007)
a link goes to–
The five entries of June 14, 2007.
From there, the link
"One Two Three Four,
Who Are We For?"
goes to–
Princeton: A Whirligig Tour
(Log24, June 5, 2007).
From there, the link
"Taking Christ to Studio 60"
goes to–
The five Log 24 entries
prior to midnight Sept. 18, 2006.
From there, the link
"Log24, January 18, 2004"
goes to–
A Living Church.
From there, the link
"click here"
goes to–
In the Bleak Midwinter
(Internet Movie Database)…
Tagline:
The drama. The passion. The intrigue… And the rehearsals haven't even started.
Plot Summary:
Out of work actor Joe volunteers to help try and save his sister's local church
for the community by putting on a Christmas production of Hamlet…
"… were it not that
I have bad dreams."
— Hamlet
Related material:
The New York Times online
obituaries of December 22,
Ike Turner's
"Bad Dreams" album
(see Log24, July 12, 2004),
"Devil Music," a composition
by H. S. M. Coxeter,
and
Those desiring more literary depth
may consult the G. K. Chesterton
play "Magic" for which Coxeter
wrote his "Devil Music" and
the Ingmar Bergman film
"The Magician" said to have
been inspired by Chesterton.
Friday, July 6, 2007
Friday July 6, 2007
of Good and Evil
continued from
Midsummer Night…
— Glenna Whitley, “Voodoo Justice,”
The New York Times, March 20, 1994

In Other Game News:
“Coxeter Exhuming Geometry”
suggests the following
illustration, based
in part on
Plato’s poem to Aster:

Related material:
and
The proportions of
the above rectangle
may suggest to some
a coffin; they are
meant to suggest
a monolith.
Thursday, May 31, 2007
Thursday May 31, 2007
Blitz by anonymous
New Delhi user
From Wikipedia on 31 May, 2007:
Shown below is a list of 25 alterations to Wikipedia math articles made today by user 122.163.102.246.
All of the alterations involve removal of links placed by user Cullinane (myself).
The 122.163… IP address is from an internet service provider in New Delhi, India.
The New Delhi anonymous user was apparently inspired by an earlier blitz by Wikipedia administrator Charles Matthews. (See User talk: Cullinane.)
Related material:
Ashay Dharwadker and Usenet Postings
and Talk: Four color theorem/Archive 2.
See also some recent comments from 122.163…
at Talk: Four color theorem.
May 31, 2007, alterations by
user 122.163.102.246:
- 17:17 Orthogonality (rm spam)
- 17:16 Symmetry group (rm spam)
- 17:14 Boolean algebra (rm spam)
- 17:12 Permutation (rm spam)
- 17:10 Boolean logic (rm spam)
- 17:08 Gestalt psychology (rm spam)
- 17:05 Tesseract (rm spam)
- 17:02 Square (geometry) (rm spam)
- 17:00 Fano plane (rm spam)
- 16:55 Binary Golay code (rm spam)
- 16:53 Finite group (rm spam)
- 16:52 Quaternion group (rm spam)
- 16:50 Logical connective (rm spam)
- 16:48 Mathieu group (rm spam)
- 16:45 Tutte–Coxeter graph (rm spam)
- 16:42 Steiner system (rm spam)
- 16:40 Kaleidoscope (rm spam)
- 16:38 Efforts to Create A Glass Bead Game (rm spam)
- 16:36 Block design (rm spam)
- 16:35 Walsh function (rm spam)
- 16:24 Latin square (rm spam)
- 16:21 Finite geometry (rm spam)
- 16:17 PSL(2,7) (rm spam)
- 16:14 Translation plane (rm spam)
- 16:13 Block design test (rm spam)
The deletions should please Charles Matthews and fans of Ashay Dharwadker’s work as a four-color theorem enthusiast and as editor of the Open Directory sections on combinatorics and on graph theory.
There seems little point in protesting the deletions while Wikipedia still allows any anonymous user to change their articles.
— Cullinane 23:28, 31 May 2007 (UTC)

























































































