"Galois space" is now a domain name: galois.space.
Friday, April 3, 2020
Sunday, November 19, 2017
Galois Space
This is a sequel to yesterday's post Cube Space Continued.
Tuesday, May 31, 2016
Tuesday, January 12, 2016
Harmonic Analysis and Galois Spaces

The above sketch indicates, in a vague, hand-waving, fashion,
a connection between Galois spaces and harmonic analysis.
For more details of the connection, see (for instance) yesterday
afternoon's post Space Oddity.
Sunday, March 10, 2013
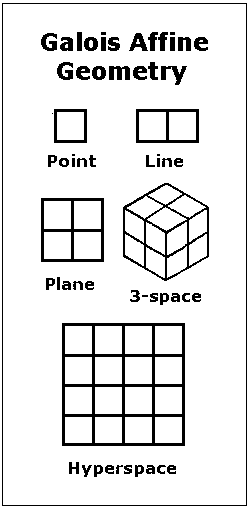
Galois Space
The 16-point affine Galois space:
Further properties of this space:
In Configurations and Squares, see the
discusssion of the Kummer 166 configuration.
Some closely related material:
- Wolfgang Kühnel,
"Minimal Triangulations of Kummer Varieties,"
Abh. Math. Sem. Univ. Hamburg 57, 7-20 (1986).For the first two pages, click here.
- Jonathan Spreer and Wolfgang Kühnel,
"Combinatorial Properties of the K 3 Surface:
Simplicial Blowups and Slicings,"
preprint, 26 pages. (2009/10) (pdf).
(Published in Experimental Math. 20,
issue 2, 201–216 (2011).)
Monday, March 4, 2013
Occupy Galois Space
Continued from February 27, the day Joseph Frank died…
"Throughout the 1940s, he published essays
and criticism in literary journals, and one,
'Spatial Form in Modern Literature'—
a discussion of experimental treatments
of space and time by Eliot, Joyce, Proust,
Pound and others— published in
The Sewanee Review in 1945, propelled him
to prominence as a theoretician."
— Bruce Weber in this morning's print copy
of The New York Times (p. A15, NY edition)
That essay is reprinted in a 1991 collection
of Frank's work from Rutgers University Press:
See also Galois Space and Occupy Space in this journal.
Frank was best known as a biographer of Dostoevsky.
A very loosely related reference… in a recent Log24 post,
Freeman Dyson's praise of a book on the history of
mathematics and religion in Russia:
"The intellectual drama will attract readers
who are interested in mystical religion
and the foundations of mathematics.
The personal drama will attract readers
who are interested in a human tragedy
with characters who met their fates with
exceptional courage."
Frank is survived by, among others, his wife, a mathematician.
Thursday, February 21, 2013
Galois Space
The previous post suggests two sayings:
"There is such a thing as a Galois space."
— Adapted from Madeleine L'Engle
"For every kind of vampire, there is a kind of cross."
Illustrations—
Thursday, July 12, 2012
Galois Space
An example of lines in a Galois space * —
The 35 lines in the 3-dimensional Galois projective space PG(3,2)—
There are 15 different individual linear diagrams in the figure above.
These are the points of the Galois space PG(3,2). Each 3-set of linear diagrams
represents the structure of one of the 35 4×4 arrays and also represents a line
of the projective space.
The symmetry of the linear diagrams accounts for the symmetry of the
840 possible images in the kaleidoscope puzzle.
* For further details on the phrase "Galois space," see
Beniamino Segre's "On Galois Geometries," Proceedings of the
International Congress of Mathematicians, 1958 [Edinburgh].
(Cambridge U. Press, 1960, 488-499.)
(Update of Jan. 5, 2013— This post has been added to finitegeometry.org.)
Friday, November 10, 2023
Logos

Related art —
(For some backstory, see Geometry of the I Ching
and the history of Chinese philosophy.)
Sunday, August 6, 2023
Contra Gombrich
A search in this journal for Cornell + Warburg suggests
a review of the concept "iconology of the interval " . . .
Ikonologie des Zwischenraums —
"Yet if this Denkraum , this 'twilight region,' is where the artist and
emblem-maker invent, then, as Gombrich well knew, Warburg also
constantly regrets the 'loss' of this 'thought-space,' which he also
dubs the Zwischenraum and Wunschraum ."
— Memory, Metaphor, and Aby Warburg's Atlas of Images ,
Christopher D. Johnson, Cornell University Press, 2012, p. 56
Sunday, June 4, 2023
The Galois Core
Monday, February 27, 2023
Friday, December 30, 2022
Bullshit Studies: The View from East Lansing
Detail of the above screen (click to enlarge) —
See also this journal on the above date — June 10, 2021.
From this journal on May 6, 2009 —
A related picture of images that "reappear metamorphosed
in the coordinate system of the high region" —
(For the backstory, see Geometry of the I Ching
and the history of Chinese philosophy.)
Friday, May 27, 2022
Great Escapes

The above scene from "Hanna" comes from a webpage
dated August 29, 2011. See also …
Tuesday, October 20, 2020
The Leibniz Methods
Click medal for some background. The medal may be regarded
as illustrating the 16-point Galois space.
Thursday, March 5, 2020
“Generated by Reflections”
See the title in this journal.
Such generation occurs both in Euclidean space …
… and in some Galois spaces —
In Galois spaces, some care must be taken in defining "reflection."
Monday, December 2, 2019
Aesthetics at Harvard
"What the piece of art is about is the gray space in the middle."
— David Bowie, as quoted in the above Crimson piece.
Bowie's "gray space" is the space between the art and the beholder.
I prefer the gray space in the following figure —
Context: The Trinity Stone (Log24, June 4, 2018).
Monday, October 15, 2018
For Zingari Shoolerim*
The structure at top right is that of the
ROMA-ORAM-MARO-AMOR square
in the previous post.
* "Zingari shoolerim" is from
Finnegans Wake .
Saturday, September 29, 2018
“Ikonologie des Zwischenraums”
The title is from Warburg. The Zwischenraum lines and shaded "cuts"
below are to be added together in characteristic two, i.e., via the
set-theoretic symmetric difference operator.
Monday, August 27, 2018
Geometry and Simplicity
From …
Thinking in Four Dimensions
By Dusa McDuff
"I’ve got the rather foolhardy idea of trying to explain
to you the kind of mathematics I do, and the kind of
ideas that seem simple to me. For me, the search
for simplicity is almost synonymous with the search
for structure.
I’m a geometer and topologist, which means that
I study the structure of space …
. . . .
In each dimension there is a simplest space
called Euclidean space … "
— In Roman Kossak, ed.,
Simplicity: Ideals of Practice in Mathematics and the Arts
(Kindle Locations 705-710, 735). Kindle Edition.
For some much simpler spaces of various
dimensions, see Galois Space in this journal.
Monday, June 4, 2018
The Trinity Stone Defined
“Unsheathe your dagger definitions.” — James Joyce, Ulysses
The “triple cross” link in the previous post referenced the eightfold cube
as a structure that might be called the trinity stone .
Sunday, March 4, 2018
The Square Inch Space: A Brief History
Friday, September 15, 2017
Space Art
Silas in "Equals" (2015) —
Ever since we were kids it's been drilled into us that …
Our purpose is to explore the universe, you know.
Outer space is where we'll find …
… the answers to why we're here and …
… and where we come from.
Related material —
See also Galois Space in this journal.
Tuesday, May 2, 2017
Image Albums
Pinterest boards uploaded to the new m759.net/piwigo —
Update of May 2 —
Update of May 3 —
Update of May 8 —
Art Space board created at Pinterest
Saturday, June 18, 2016
Midnight in Herald Square
In memory of New Yorker artist Anatol Kovarsky,
who reportedly died at 97 on June 1.

Note the Santa, a figure associated with Macy's at Herald Square.
See also posts tagged Herald Square, as well as the following
figure from this journal on the day preceding Kovarsky's death.

A note related both to Galois space and to
the "Herald Square"-tagged posts —

"There is such a thing as a length-16 sequence."
— Saying adapted from a young-adult novel.
Sunday, May 8, 2016
The Three Solomons
Earlier posts have dealt with Solomon Marcus and Solomon Golomb,
both of whom died this year — Marcus on Saint Patrick's Day, and
Golomb on Orthodox Easter Sunday. This suggests a review of
Solomon LeWitt, who died on Catholic Easter Sunday, 2007.
A quote from LeWitt indicates the depth of the word "conceptual"
in his approach to "conceptual art."
|
From Sol LeWitt: A Retrospective , edited by Gary Garrels, Yale University Press, 2000, p. 376:
THE SQUARE AND THE CUBE "The best that can be said for either the square or the cube is that they are relatively uninteresting in themselves. Being basic representations of two- and three-dimensional form, they lack the expressive force of other more interesting forms and shapes. They are standard and universally recognized, no initiation being required of the viewer; it is immediately evident that a square is a square and a cube a cube. Released from the necessity of being significant in themselves, they can be better used as grammatical devices from which the work may proceed." "Reprinted from Lucy R. Lippard et al ., “Homage to the Square,” Art in America 55, No. 4 (July-August 1967): 54. (LeWitt’s contribution was originally untitled.)" |
See also the Cullinane models of some small Galois spaces —
Friday, May 6, 2016
Monday, January 11, 2016
Space Oddity
It is an odd fact that the close relationship between some
small Galois spaces and small Boolean spaces has gone
unremarked by mathematicians.
A Google search today for “Galois spaces” + “Boolean spaces”
yielded, apart from merely terminological sources, only some
introductory material I have put on the Web myself.
Some more sophisticated searches, however led to a few
documents from the years 1971 – 1981 …
“Harmonic Analysis of Switching Functions” ,
by Robert J. Lechner, Ch. 5 in A. Mukhopadhyay, editor,
Recent Developments in Switching Theory , Academic Press, 1971.
“Galois Switching Functions and Their Applications,”
by B. Benjauthrit and I. S. Reed,
JPL Deep Space Network Progress Report 42-27 , 1975
D.K. Pradhan, “A Theory of Galois Switching Functions,”
IEEE Trans. Computers , vol. 27, no. 3, pp. 239-249, Mar. 1978
“Switching functions constructed by Galois extension fields,”
by Iwaro Takahashi, Information and Control ,
Volume 48, Issue 2, pp. 95–108, February 1981
An illustration from the Lechner paper above —

“There is such a thing as harmonic analysis of switching functions.”
— Saying adapted from a young-adult novel
Wednesday, October 21, 2015
Algebra and Space
"Perhaps an insane conceit …." Perhaps.
Related remarks on algebra and space —
"The Quality Without a Name" (Log24, August 26, 2015).
Friday, August 14, 2015
Discrete Space
(A review)
Galois space:
Counting symmetries of Galois space:

The reason for these graphic symmetries in affine Galois space —
symmetries of the underlying projective Galois space:
Monday, January 5, 2015
Gitterkrieg*
Wednesday, March 13, 2013
|
"I pondered deeply, then, over the
adventures of the jungle. And after
some work with a colored pencil
I succeeded in making my first drawing.
My Drawing Number One.
It looked something like this:
I showed my masterpiece to the
grown-ups, and asked them whether
the drawing frightened them.
But they answered: 'Why should
anyone be frightened by a hat?'"
* For the title, see Plato Thanks the Academy (Jan. 3).
Monday, September 22, 2014
Sunday, September 14, 2014
Sensibility
Structured gray matter:

Graphic symmetries of Galois space:

The reason for these graphic symmetries in affine Galois space —
symmetries of the underlying projective Galois space:
Sunday, August 31, 2014
Sunday School
The Folding
Cynthia Zarin in The New Yorker , issue dated April 12, 2004—
“Time, for L’Engle, is accordion-pleated. She elaborated,
‘When you bring a sheet off the line, you can’t handle it
until it’s folded, and in a sense, I think, the universe can’t
exist until it’s folded — or it’s a story without a book.’”
The geometry of the 4×4 square array is that of the
3-dimensional projective Galois space PG(3,2).
This space occurs, notably, in the Miracle Octad Generator (MOG)
of R. T. Curtis (submitted to Math. Proc. Camb. Phil. Soc. on
15 June 1974). Curtis did not, however, describe its geometric
properties. For these, see the Cullinane diamond theorem.
Some history:
Curtis seems to have obtained the 4×4 space by permuting,
then “folding” 1×8 binary sequences into 4×2 binary arrays.
The original 1×8 sequences came from the method of Turyn
(1967) described by van Lint in his book Coding Theory
(Springer Lecture Notes in Mathematics, No. 201 , first edition
published in 1971). Two 4×2 arrays form each 4×4 square array
within the MOG. This construction did not suggest any discussion
of the geometric properties of the square arrays.
[Rewritten for clarity on Sept. 3, 2014.]
Thursday, July 17, 2014
Paradigm Shift:
Continuous Euclidean space to discrete Galois space*
Euclidean space:
Counting symmetries in Euclidean space:
Galois space:
Counting symmetries of Galois space:

The reason for these graphic symmetries in affine Galois space —
symmetries of the underlying projective Galois space:
* For related remarks, see posts of May 26-28, 2012.
Wednesday, July 16, 2014
Wednesday, May 21, 2014
Through the Vanishing Point*
Marshall McLuhan in "Annie Hall" —
"You know nothing of my work."
Related material —
"I need a photo opportunity
I want a shot at redemption
Don't want to end up a cartoon
In a cartoon graveyard"
— Paul Simon
It was a dark and stormy night…

— Page 180, Logicomix
A photo opportunity for Whitehead
(from Romancing the Cube, April 20, 2011)—
See also Absolute Ambition (Nov. 19, 2010).
* For the title, see Vanishing Point in this journal.
Friday, March 21, 2014
Three Constructions of the Miracle Octad Generator
See also a Log24 post on this subject from Dec. 14, 2013,
especially (scroll down) the update of March 9, 2014.
Related material on the Turyn-Curtis construction
from the University of Cambridge —

— Slide by "Dr. Parker" — Apparently Richard A. Parker —
Lecture 4, "Discovering M24," in slides for lectures 1-8 from lectures
at Cambridge in 2010-2011 on "Sporadic and Related Groups."
See also the Parker lectures of 2012-2013 on the same topic.
A third construction of Curtis's 35 4×6 1976 MOG arrays would use
Cullinane's analysis of the 4×4 subarrays' affine and projective structure,
and point out the fact that Conwell's 1910 correspondence of the 35
4+4-partitions of an 8-set with the 35 lines of the projective 3-space
over the 2-element field, PG(3, 2), is essentially the same correspondence
as that constituting Curtis's 1976 MOG.
See The Diamond Theorem, Finite Relativity, Galois Space,
Generating the Octad Generator, and The Klein Correspondence.
Update of March 22-March 23 —
Adding together as (0,1)-matrices over GF(2) the black parts (black
squares as 1's, all other squares as 0's) of the 35 4×6 arrays of the 1976
Curtis MOG would then reveal* the symmetric role played in octads
by what Curtis called the heavy brick , and so reveal also the action of
S3 on the three Curtis bricks that leaves invariant the set of all 759
octads of the S(5, 8, 24) constructed from the 35 MOG arrays. For more
details of this "by-hand" construction, see Geometry of the 4×4 Square.
For the mathematical properties of the S(5, 8, 24), it is convenient to
have a separate construction (such as Turyn's), not by hand, of the
extended binary Golay code. See the Brouwer preprint quoted above.
* "Then a miracle occurs," as in the classic 1977 Sidney Harris cartoon.
Illustration of array addition from March 23 —
Friday, March 7, 2014
Kummer Varieties
The Dream of the Expanded Field continues…
From Klein's 1893 Lectures on Mathematics —

"The varieties introduced by Wirtinger may be called Kummer varieties…."
— E. Spanier, 1956
From this journal on March 10, 2013 —
From a recent paper on Kummer varieties,
arXiv:1208.1229v3 [math.AG] 12 Jun 2013,
"The Universal Kummer Threefold," by
Qingchun Ren, Steven V Sam, Gus Schrader, and Bernd Sturmfels —

Two such considerations —
Update of 10 PM ET March 7, 2014 —
The following slides by one of the "Kummer Threefold" authors give
some background related to the above 64-point vector space and
to the Weyl group of type E7, W (E7):
The Cayley reference is to "Algorithm for the characteristics of the
triple ϑ-functions," Journal für die Reine und Angewandte
Mathematik 87 (1879): 165-169. <http://eudml.org/doc/148412>.
To read this in the context of Cayley's other work, see pp. 441-445
of Volume 10 of his Collected Mathematical Papers .
Wednesday, February 5, 2014
Mystery Box II
Continued from previous post and from Sept. 8, 2009.

Examination of the box's contents does not solve
the contents' real mystery. That requires knowledge
of the non-Euclidean geometry of Galois space.
In this case, without that knowledge, prattle (as in
today's online New York Times ) about creativity and
"thinking outside the box" is pointless.
Tuesday, December 3, 2013
Diamond Space
A new website illustrates its URL.
See DiamondSpace.net.
Thursday, November 7, 2013
Pattern Grammar
Yesterday afternoon's post linked to efforts by
the late Robert de Marrais to defend a mathematical
approach to structuralism and kaleidoscopic patterns.
Two examples of non-mathematical discourse on
such patterns:
1. A Royal Society paper from 2012—
Click the above image for related material in this journal.
2. A book by Junichi Toyota from 2009—
Kaleidoscopic Grammar: Investigation into the Nature of Binarism
I find such non-mathematical approaches much less interesting
than those based on the mathematics of reflection groups .
De Marrais described the approaches of Vladimir Arnold and,
earlier, of H. S. M. Coxeter, to such groups. These approaches
dealt only with groups of reflections in Euclidean spaces.
My own interest is in groups of reflections in Galois spaces.
See, for instance, A Simple Reflection Group of Order 168.
Galois spaces over fields of characteristic 2 are particularly
relevant to what Toyota calls binarism .
Thursday, July 4, 2013
Declaration of Independent
"Classical Geometry in Light of Galois Geometry"
is now available at independent.academia.edu.
Related commentary: Yesterday's post Vision
and a post of February 21, 2013: Galois Space.
Saturday, March 16, 2013
The Crosswicks Curse
From the prologue to the new Joyce Carol Oates
novel Accursed—
"This journey I undertake with such anticipation
is not one of geographical space but one of Time—
for it is the year 1905 that is my destination.
1905!—the very year of the Curse."
Today's previous post supplied a fanciful link
between the Crosswicks Curse of Oates and
the Crosswicks tesseract of Madeleine L'Engle.
The Crosswicks Curse according to L'Engle
in her classic 1962 novel A Wrinkle in Time —
"There is such a thing as a tesseract."
A tesseract is a 4-dimensional hypercube that
(as pointed out by Coxeter in 1950) may also
be viewed as a 4×4 array (with opposite edges
identified).
Meanwhile, back in 1905…
For more details, see how the Rosenhain and Göpel tetrads occur naturally
in the diamond theorem model of the 35 lines of the 15-point projective
Galois space PG(3,2).
See also Conwell in this journal and George Macfeely Conwell in the
honors list of the Princeton Class of 1905.
Wednesday, March 13, 2013
Blackboard Jungle
From a review in the April 2013 issue of
Notices of the American Mathematical Society—
"The author clearly is passionate about mathematics
as an art, as a creative process. In reading this book,
one can easily get the impression that mathematics
instruction should be more like an unfettered journey
into a jungle where an individual can make his or her
own way through that terrain."
From the book under review—
"Every morning you take your machete into the jungle
and explore and make observations, and every day
you fall more in love with the richness and splendor
of the place."
— Lockhart, Paul (2009-04-01). A Mathematician's Lament:
How School Cheats Us Out of Our Most Fascinating and
Imaginative Art Form (p. 92). Bellevue Literary Press.
Kindle Edition.
Related material: Blackboard Jungle in this journal.
See also Galois Space and Solomon's Mines.
Wednesday, March 6, 2013
Midnight in Pynchon*
"It is almost as though Pynchon wishes to
repeat the grand gesture of Joyce’s Ulysses…."
— Vladimir Tasic on Pynchon's Against the Day
Related material:
Tasic's Mathematics and the Roots of Postmodern Thought
and Michael Harris's "'Why Mathematics?' You Might Ask"
*See also Occupy Galois Space and Midnight in Dostoevsky.
Tuesday, February 19, 2013
Configurations
Yesterday's post Permanence dealt with the cube
as a symmetric model of the finite projective plane
PG(2,3), which has 13 points and 13 lines. The points
and lines of the finite geometry occur in the cube as
the 13 axes of symmetry and the 13 planes through
the center perpendicular to those axes. If the three
axes lying in a plane that cuts the cube in a hexagon
are supplemented by the axis perpendicular to that
plane, each plane is associated with four axes and,
dually, each axis is associated with four planes.
My web page on this topic, Cubist Geometries, was
written on February 27, 2010, and first saved to the
Internet Archive on Oct. 4, 2010.
For a more recent treatment of this topic that makes
exactly the same points as the 2010 page, see p. 218
of Configurations from a Graphical Viewpoint , by
Tomaž Pisanski and Brigitte Servatius, published by
Springer on Sept. 23, 2012 (date from both Google
Books and Amazon.com):
For a similar 1998 treatment of the topic, see Burkard Polster's
A Geometrical Picture Book (Springer, 1998), pp. 103-104.
The Pisanski-Servatius book reinforces my argument of Jan. 13, 2013,
that the 13 planes through the cube's center that are perpendicular
to the 13 axes of symmetry of the cube should be called the cube's
symmetry planes , contradicting the usual use of of that term.
That argument concerns the interplay between Euclidean and
Galois geometry. Pisanski and Servatius (and, in 1998, Polster)
emphasize the Euclidean square and cube as guides* to
describing the structure of a Galois space. My Jan. 13 argument
uses Galois structures as a guide to re-describing those of Euclid .
(For a similar strategy at a much more sophisticated level,
see a recent Harvard Math Table.)
Related material: Remarks on configurations in this journal
during the month that saw publication of the Pisanski-Servatius book.
* Earlier guides: the diamond theorem (1978), similar theorems for
2x2x2 (1984) and 4x4x4 cubes (1983), and Visualizing GL(2,p)
(1985). See also Spaces as Hypercubes (2012).
Wednesday, January 16, 2013
Medals
National…
International…
Click medal for some background. The medal may be regarded
as illustrating the 16-point Galois space. (See previous post.)
Related material: Jews in Hyperspace.
Saturday, January 5, 2013
Vector Addition in a Finite Field
The finite (i.e., Galois) field GF(16),
according to J. J. Seidel in 1974—
The same field according to Steven H. Cullinane in 1986,
in its guise as the affine 4-space over GF(2)—

The same field, again disguised as an affine 4-space,
according to John H. Conway and N.J.A. Sloane in
Sphere Packings, Lattices, and Groups , first published in 1988—

The above figure by Conway and Sloane summarizes, using
a 4×4 array, the additive vector-space structure of the finite
field GF(16).
This structure embodies what in Euclidean space is called
the parallelogram rule for vector addition—

(Thanks to June Lester for the 3D (uvw) part of the above figure.)
For the transition from this colored Euclidean hypercube
(used above to illustrate the parallelogram rule) to the
4×4 Galois space (illustrated by Cullinane in 1979 and
Conway and Sloane in 1988— or later… I do not have
their book’s first edition), see Diamond Theory in 1937,
Vertex Adjacency in a Tesseract and in a 4×4 Array,
Spaces as Hypercubes, and The Galois Tesseract.
For some related narrative, see tesseract in this journal.
(This post has been added to finitegeometry.org.)
Update of August 9, 2013—
Coordinates for hypercube vertices derived from the
parallelogram rule in four dimensions were better
illustrated by Jürgen Köller in a web page archived in 2002.
Update of August 13, 2013—
The four basis vectors in the 2002 Köller hypercube figure
are also visible at the bottom of the hypercube figure on
page 7 of “Diamond Theory,” excerpts from a 1976 preprint
in Computer Graphics and Art , Vol. 2, No. 1, February 1977.
A predecessor: Coxeter’s 1950 hypercube figure from
“Self-Dual Configurations and Regular Graphs.”
Monday, August 29, 2011
Many = Six.
A comment today on yesterday's New York Times philosophy column "The Stone"
notes that "Augustine… incorporated Greek ideas of perfection into Christianity."
Yesterday's post here for the Feast of St. Augustine discussed the 2×2×2 cube.
Today's Augustine comment in the Times reflects (through a glass darkly)
a Log24 post from Augustine's Day, 2006, that discusses the larger 4×4×4 cube.
For related material, those who prefer narrative to philosophy may consult
Charles Williams's 1931 novel Many Dimensions . Those who prefer mathematics
to either may consult an interpretation in which Many = Six.
Click image for some background.
Tuesday, May 10, 2011
Groups Acting
The LA Times on last weekend's film "Thor"—
"… the film… attempts to bridge director Kenneth Branagh's high-minded Shakespearean intentions with Marvel Entertainment's bottom-line-oriented need to crank out entertainment product."
Those averse to Nordic religion may contemplate a different approach to entertainment (such as Taymor's recent approach to Spider-Man).
A high-minded— if not Shakespearean— non-Nordic approach to groups acting—
"What was wrong? I had taken almost four semesters of algebra in college. I had read every page of Herstein, tried every exercise. Somehow, a message had been lost on me. Groups act . The elements of a group do not have to just sit there, abstract and implacable; they can do things, they can 'produce changes.' In particular, groups arise naturally as the symmetries of a set with structure. And if a group is given abstractly, such as the fundamental group of a simplical complex or a presentation in terms of generators and relators, then it might be a good idea to find something for the group to act on, such as the universal covering space or a graph."
— Thomas W. Tucker, review of Lyndon's Groups and Geometry in The American Mathematical Monthly , Vol. 94, No. 4 (April 1987), pp. 392-394
"Groups act "… For some examples, see
- The 2×2×2 Cube,
- The Diamond 16 Puzzle,
- The Diamond Theorem, and
- Finite Geometry of the Square and Cube.
Related entertainment—
High-minded— Many Dimensions—

Not so high-minded— The Cosmic Cube—

One way of blending high and low—
The high-minded Charles Williams tells a story
in his novel Many Dimensions about a cosmically
significant cube inscribed with the Tetragrammaton—
the name, in Hebrew, of God.
The following figure can be interpreted as
the Hebrew letter Aleph inscribed in a 3×3 square—
The above illustration is from undated software by Ed Pegg Jr.
For mathematical background, see a 1985 note, "Visualizing GL(2,p)."
For entertainment purposes, that note can be generalized from square to cube
(as Pegg does with his "GL(3,3)" software button).
For the Nordic-averse, some background on the Hebrew connection—
Saturday, August 7, 2010
The Matrix Reloaded
For aficionados of mathematics and narrative —
Illustration from
"The Galois Quaternion— A Story"
This resembles an attempt by Coxeter in 1950 to represent
a Galois geometry in the Euclidean plane—
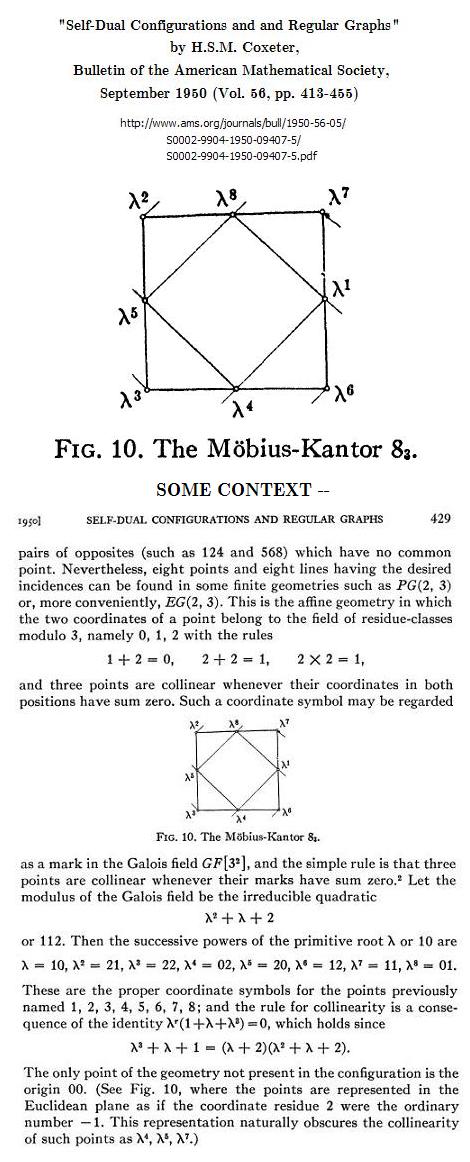
The quaternion illustration above shows a more natural way to picture this geometry—
not with dots representing points in the Euclidean plane, but rather with unit squares
representing points in a finite Galois affine plane. The use of unit squares to
represent points in Galois space allows, in at least some cases, the actions
of finite groups to be represented more naturally than in Euclidean space.
See Galois Geometry, Geometry Simplified, and
Finite Geometry of the Square and Cube.
Saturday, June 19, 2010
Imago Creationis
In the above view, four of the tesseract's 16
vertices are overlaid by other vertices.
For views that are more complete and
moveable, see Smith's tesseract page.
Four-Part Tesseract Divisions—

The above figure shows how four-part partitions
of the 16 vertices of a tesseract in an infinite
Euclidean space are related to four-part partitions
of the 16 points in a finite Galois space
|
Euclidean spaces versus Galois spaces in a larger context—
Infinite versus Finite The central aim of Western religion —
"Each of us has something to offer the Creator...
the bridging of
masculine and feminine,
life and death.
It's redemption.... nothing else matters."
-- Martha Cooley in The Archivist (1998)
The central aim of Western philosophy —
Dualities of Pythagoras
as reconstructed by Aristotle:
Limited Unlimited
Odd Even
Male Female
Light Dark
Straight Curved
... and so on ....
"Of these dualities, the first is the most important; all the others may be seen as different aspects of this fundamental dichotomy. To establish a rational and consistent relationship between the limited [man, etc.] and the unlimited [the cosmos, etc.] is… the central aim of all Western philosophy." |
Another picture related to philosophy and religion—
Jung's Four-Diamond Figure from Aion—

This figure was devised by Jung
to represent the Self. Compare the
remarks of Paul Valéry on the Self—
|
Flight from Eden: The Origins of Modern Literary Criticism and Theory, by Steven Cassedy, U. of California Press, 1990, pages 156-157—
Valéry saw the mind as essentially a relational system whose operation he attempted to describe in the language of group mathematics. "Every act of understanding is based on a group," he says (C, 1:331). "My specialty— reducing everything to the study of a system closed on itself and finite" (C, 19: 645). The transformation model came into play, too. At each moment of mental life the mind is like a group, or relational system, but since mental life is continuous over time, one "group" undergoes a "transformation" and becomes a different group in the next moment. If the mind is constantly being transformed, how do we account for the continuity of the self? Simple; by invoking the notion of the invariant. And so we find passages like this one: "The S[elf] is invariant, origin, locus or field, it's a functional property of consciousness" (C, 15:170 [2:315]). Just as in transformational geometry, something remains fixed in all the projective transformations of the mind's momentary systems, and that something is the Self (le Moi, or just M, as Valéry notates it so that it will look like an algebraic variable). Transformation theory is all over the place. "Mathematical science… reduced to algebra, that is, to the analysis of the transformations of a purely differential being made up of homogeneous elements, is the most faithful document of the properties of grouping, disjunction, and variation in the mind" (O, 1:36). "Psychology is a theory of transformations, we just need to isolate the invariants and the groups" (C, 1:915). "Man is a system that transforms itself" (C, 2:896). O Paul Valéry, Oeuvres (Paris: Pléiade, 1957-60) C Valéry, Cahiers, 29 vols. (Paris: Centre National de le Recherche Scientifique, 1957-61) |
Note also the remarks of George David Birkhoff at Rice University
in 1940 (pdf) on Galois's theory of groups and the related
"theory of ambiguity" in Galois's testamentary letter—
|
… metaphysical reasoning always relies on the Principle of Sufficient Reason, and… the true meaning of this Principle is to be found in the “Theory of Ambiguity” and in the associated mathematical “Theory of Groups.” If I were a Leibnizian mystic, believing in his “preestablished harmony,” and the “best possible world” so satirized by Voltaire in “Candide,” I would say that the metaphysical importance of the Principle of Sufficient Reason and the cognate Theory of Groups arises from the fact that God thinks multi-dimensionally* whereas men can only think in linear syllogistic series, and the Theory of Groups is the appropriate instrument of thought to remedy our deficiency in this respect. * That is, uses multi-dimensional symbols beyond our grasp. |
Related material:
A medal designed by Leibniz to show how
binary arithmetic mirrors the creation by God
of something (1) from nothing (0).

Another array of 16 strings of 0's and 1's, this time
regarded as coordinates rather than binary numbers—


Some context by a British mathematician —

|
Imago by Wallace Stevens Who can pick up the weight of Britain, Who can move the German load Or say to the French here is France again? Imago. Imago. Imago. It is nothing, no great thing, nor man Of ten brilliancies of battered gold And fortunate stone. It moves its parade Of motions in the mind and heart, A gorgeous fortitude. Medium man In February hears the imagination's hymns And sees its images, its motions And multitudes of motions And feels the imagination's mercies, In a season more than sun and south wind, Something returning from a deeper quarter, A glacier running through delirium, Making this heavy rock a place, Which is not of our lives composed . . . Lightly and lightly, O my land, Move lightly through the air again. |
Wednesday, May 6, 2009
Wednesday May 6, 2009
“My pursuits are a joke
in that the universe is a joke.
One has to reflect
the universe faithfully.”
— John Frederick Michell
Feb. 9, 1933 –
April 24, 2009
This is a crazy world and
the only way to enjoy it
is to treat it as a joke.”
— Robert A. Heinlein,
The Number of the Beast
For Marisa Tomei
(born Dec. 4, 1964) —
on the day that
Bob Seger turns 64 —
A Joke:
Points All Her Own
Points All Her Own,
Part I:
(For the backstory, see
the Log24 entries and links
on Marisa Tomei’s birthday
last year.)

Points All Her Own,
Part II:
(For the backstory, see
Galois Geometry:
The Simplest Examples.)

Points All Her Own,
Part III:
(For the backstory, see
Geometry of the I Ching
and the history of
Chinese philosophy.)
In simpler terms:







_lines_as_arrays-500w.jpg)