At https://shc759.wordpress.com today —
For a much larger view of this topic, see other posts in this journal
tagged Cullinane Cube. For a large (16 MB) downloadable
document containing these posts, see . . .
log24.com/log24/240222-Log24-posts-tagged-Cullinane-Cube.pdf.
From a post on Trevanian in December 2005 —
"And we may see
the meadow in December,
icy white and crystalline."
In memory of a former president of Boston University —
Other posts now tagged Cube Mine.
Related entertainment —
The Replit code development environment featured
in today's previous post has hosted, for some time now,
an embodiment of the design cube from earlier posts —
For the late Brian O'Doherty, from posts now tagged "Pless Birthday 2022" —
This post was suggested by an obituary of O'Doherty and by
"The Life and Work of Vera Stepen Pless" in
Notices of the American Mathematical Society , December 2022.
At Hiroshima on March 9, 2018, Aitchison discussed another
"hexagonal array" with two added points… not at the center, but
rather at the ends of a cube's diagonal axis of symmetry.
See some related illustrations below.
Fans of the fictional "Transfiguration College" in the play
"Heroes of the Fourth Turning" may recall that August 6,
another Hiroshima date, was the Feast of the Transfiguration.
The exceptional role of 0 and ∞ in Aitchison's diagram is echoed
by the occurence of these symbols in the "knight" labeling of a
Miracle Octad Generator octad —
Transposition of 0 and ∞ in the knight coordinatization
induces the symplectic polarity of PG(3,2) discussed by
(for instance) Anne Duncan in 1968.
From a Toronto Star video on the Langlands program —
From a review of the 2017 film "Justice League" —
"Now all they need is to resurrect Superman (Henry Cavill),
stop Steppenwolf from reuniting his three Mother Cubes
(sure, whatever) and wrap things up in under two cinematic
hours (God bless)."
See also the 2018 film "Avengers of Justice: Farce Wars."
Cartoon version of George Eliot, author of Middlemarch ,
and Ada Lovelace, programming pioneer —
See as well an earlier vision of a data cube for mythologies
by Claude Lévi-Strauss —
From the 2019 post Spring Loaded —
A more recent image, from Carroll's wife Jennifer Ouellette —
For a more sophisticated approach to the 4x4x4 cube,
see a page at finitegeometry.org.
The new URL supercube.space forwards to http://box759.wordpress.com/.
The term supercube is from a 1982 article by Solomon W. Golomb.
The related new URL supercube.group forwards to a page that
describes how the 2x2x2 (or eightfold, or "super") cube's natural
underlying automorphism group is Klein's simple group of order 168.
For further context, see the new URL supercube.art.
For some background, see the phrase Cube Space in this journal.
See Sith Pyramid and Jedi Cube .
Related reading . . .
Pyramid:
https://www.theguardian.com/commentisfree/
2022/feb/27/vladimir-putin-russia-ukraine-power
Cube:
"To enter into the world of Putin’s favorite philosophers
is to enter a world full of melodrama, mysticism and
grandiose eschatological visions."
— David Brooks in the online New York Times on March 3, 2014
Scholium:
This journal on the above NY Times date —
Shown below is an illustration from "The Puzzle Layout Problem" —
Exercise: Using the above numerals 1 through 24
(with 23 as 0 and 24 as ∞) to represent the points
∞, 0, 1, 2, 3 … 22 of the projective line over GF(23),
reposition the labels 1 through 24 in the above illustration
so that they appropriately* illustrate the cube-parts discussed
by Iain Aitchison in his March 2018 Hiroshima slides on
cube-part permutations by the Mathieu group M24.
A note for Northrop Frye —
Interpenetration in the eightfold cube — the three midplanes —
A deeper example of interpenetration:
Aitchison has shown that the Mathieu group M24 has a natural
action on the 24 center points of the subsquares on the eightfold
cube's six faces (four such points on each of the six faces). Thus
the 759 octads of the Steiner system S(5, 8, 24) interpenetrate
on the surface of the cube.
* "Appropriately" — I.e. , so that the Aitchison cube octads correspond
exactly, via the projective-point labels, to the Curtis MOG octads.
New York Review of Books , Dec. 16, 2021 issue —
Lorrie Moore on the documentary series "Couples Therapy" —
"Few of the people sitting on the couch avoid the cliché of
one person (a man) playing fruitlessly with a plastic puzzle
while the other speaks tearfully and avails herself of a
Kleenex box. In season 1, there is literally a Rubik’s cube,
and no one ever solves it, an unfortunate but apt metaphor.
During one session, when the cube has been placed out of reach,
one of the husbands gets up to look for it, finding it on a shelf."
See also . . .
"The bond with reality is cut." — Hans Freudenthal
The above Quanta article mentions
"Maryna Viazovska’s 2016 discovery of the most efficient
ways of packing spheres in dimensions eight and 24."
From a course to be taught by Viazovska next spring:
The Lovasz reference suggests a review of my own webpage
Cube Space, 1984-2003.
See as well a review of Log24 posts on Packing.
From the post "Games" of Jan. 31, 2021 —
“Once Knecht confessed to his teacher that he wished to
learn enough to be able to incorporate the system of the
I Ching into the Glass Bead Game. Elder Brother laughed.
‘Go ahead and try’, he exclaimed. ‘You’ll see how it turns out.
Anyone can create a pretty little bamboo garden in the world.
But I doubt the gardener would succeed in incorporating
the world in his bamboo grove’ ” (P. 139).
— Hermann Hesse, The Glass Bead Game (Magister Ludi) .
Translated by Richard and Clara Winston ( London, Vintage, 2000).
Geometry for Jews continues.
The conclusion of Solomon Golomb's
"Rubik's Cube and Quarks,"
American Scientist , May-June 1982 —
Related geometric meditation —
Archimedes at Hiroshima
in posts tagged Aitchison.
* As opposed to Solomon's Cube .
"Before time began, there was the Cube."
— Hassenfeld Brothers merchandising slogan
Related vocabulary —
See as well the word facet in this journal.
Analogously, one might write . . .
A Hiroshima cube consists of 6 faces ,
each with 4 squares called facets ,
for a total of 24 facets. . . ."
(See Aitchison's Octads , a post of Feb. 19, 2020.)
Click image to enlarge. Background: Posts tagged 'Aitchison.'"
The new domain http://cube.school
points to posts tagged Cube School here.
“WHEN I IMAGINE THE CUBE, I see a structure in motion.
I see the framework of its edges, its corners, and its flexible joints,
and the continuous transformations in front of me (before you start
to worry, I assure you that I can freeze it anytime I like). I don’t see
a static object but a system of dynamic relations. In fact, this is only
half of that system. The other half is the person who handles it.
Just like everything else in our world, a system is defined by
its place within a network of relations—to humans, first of all.”
— Rubik, Erno. Cubed (p. 165). Flatiron Books. Kindle Ed., 2020.
Compare and contrast — Adoration of the Blessed Sacrament.
For the Sith Pyramid, see posts tagged Pyramid Game.
For the Jedi Cube, see posts tagged Enigma Cube
and cube-related remarks by Aitchison at Hiroshima.
This post was suggested by two events of May 16, 2019 —
A weblog post by Frans Marcelis on the Miracle Octad
Generator of R. T. Curtis (illustrated with a pyramid),
and the death of I. M. Pei, architect of the Louvre pyramid.
That these events occurred on the same date is, of course,
completely coincidental.
Perhaps Dan Brown can write a tune to commemorate
the coincidence.
Promotional material —
“Did you buckle up?” — Harlan Kane
The publication date of The Enigma Cube reported above was February 13, 2020.
Related material — Log24 posts around that date now tagged The Reality Bond.
See also this journal on November 29, 2011 —The Flight from Ennui.
Related illustration from earlier in 2011 —
See also this journal on 20 Sept. 2011 — Relativity Problem Revisited —
as well as Congregated Light.
Exercise: Use the Guitart 7-cycles below to relate the 56 triples
in an 8-set (such as the eightfold cube) to the 56 triangles in
a well-known Klein-quartic hyperbolic-plane tiling. Then use
the correspondence of the triples with the 56 spreads of PG(3,2)
to construct M24.
Click image below to download a Guitart PowerPoint presentation.
See as well earlier posts also tagged Triangles, Spreads, Mathieu.
Metaphysical conceit | literature | Britannica.com
|
This post's title refers to a metaphysical conceit
in the previous post, Desperately Seeking Clarity.
Related material —
The source of the above mystical octahedron —
See also Jung's Imago Dei in this journal.
For affine group actions, see Ex Fano Appollinis (June 24)
and Solomon's Cube.
For one approach to Mathieu group actions on a 24-cube subset
of the 4x4x4 cube, see . . .
For a different sort of Mathieu cube, see Aitchison.
The opening lines of Eliot's Four Quartets —
"Time present and time past
Are both perhaps present in time future,
And time future contained in time past."
Perhaps.
Those who prefer geometry to rhetoric may also prefer
to Eliot's lines the immortal opening of the Transformers saga —
"Before time began, there was the Cube."
One version of the Cube —
An illustration from the April 20, 2016, post
Symmetric Generation of a Simple Group —
"The geometry of unit cubes is a meeting point
of several different subjects in mathematics."
— Chuanming Zong, Bulletin of the American
Mathematical Society , January 2005
See also Espacement and The Thing and I.
For PSL(2,7), this is ((49-1)(49-7))/((7-1)(2))=168.
The group GL(3,2), also of order 168, acts naturally
on the set of seven cube-slicings below —
Another way to picture the seven natural slicings —
Application of the above images to picturing the
isomorphism of PSL(2,7) with GL(3,2) —
.gif)
For a more detailed proof, see . . .
This journal ten years ago today —
Surprise Package
From a talk by a Melbourne mathematician on March 9, 2018 —
The source — Talk II below —
Search Results
|
Related material —
The 56 triangles of the eightfold cube . . .
Image from Christmas Day 2005.
Clicking on Zong in the above post leads to a 2005 article
in the Bulletin of the American Mathematical Society .
See also the eightfold cube and interality .
Found today in an Internet image search, from the website of
an anonymous amateur mathematics enthusiast —
Forming Gray codes in the eightfold cube with the eight
I Ching trigrams (bagua ) —
This journal on Nov. 7, 2016 —
A different sort of cube, from the makers of the recent
Netflix miniseries "Maniac" —
See also Rubik in this journal.
See also "Eternal Recreation" (Christmas Eve, 2012).
Click to enlarge:
Above are the 7 frames of an animated gif from a Wikipedia article.
* For the Furey of the title, see a July 20 Quanta Magazine piece —
See also the eightfold cube in this journal.
"Before time began . . . ." — Optimus Prime
From a post of July 25, 2008, “56 Triangles,” on the Klein quartic
and the eightfold cube —
“Baez’s discussion says that the Klein quartic’s 56 triangles
can be partitioned into 7 eight-triangle Egan ‘cubes’ that
correspond to the 7 points of the Fano plane in such a way
that automorphisms of the Klein quartic correspond to
automorphisms of the Fano plane. Show that the
56 triangles within the eightfold cube can also be partitioned
into 7 eight-triangle sets that correspond to the 7 points of the
Fano plane in such a way that (affine) transformations of the
eightfold cube induce (projective) automorphisms of the Fano plane.”
Related material from 1975 —
More recently …
From a Toronto Star video pictured here on April 1 three years ago:
The three connected cubes are labeled "Harmonic Analysis," 'Number Theory,"
and "Geometry."
Related cultural commentary from a review of the recent film "Justice League" —
"Now all they need is to resurrect Superman (Henry Cavill),
stop Steppenwolf from reuniting his three Mother Cubes
(sure, whatever) and wrap things up in under two cinematic
hours (God bless)."
The nineteenth-century German mathematician Felix Christian Klein
as Steppenwolf —
Volume I of a treatise by Klein is subtitled
"Arithmetic, Algebra, Analysis." This covers
two of the above three Toronto Star cubes.
Klein's Volume II is subtitled "Geometry."
An excerpt from that volume —
Further cultural commentary: "Glitch" in this journal.
For Greta Gerwig and Saoirse Ronan —
See also a Log24 post from the above Cube Theory date —
April 12, 2016 — Lyrics for a Cartoon Graveyard — as well as . . .
The Java applets at the webpage "Diamonds and Whirls"
that illustrate Cullinane cubes may be difficult to display.
Here instead is an animated GIF that shows the basic unit
for the "design cube" pages at finitegeometry.org.
See Eightfold Froebel.
James Propp in the current Math Horizons on the eightfold cube —
For another puerile approach to the eightfold cube,
see Cube Space, 1984-2003 (Oct. 24, 2008).
From this journal on August 18, 2015, "A Wrinkle in Terms" —
For two misuses by John Baez of the phrase “permutation group”
at the n-Category Café, see “A Wrinkle in the Mathematical Universe”
and “Re: A Wrinkle…” —
“There is such a thing as a permutation group.”
— Adapted from A Wrinkle in Time , by Madeleine L’Engle
* See RIP, Time Cube at gizmodo.com (September 1, 2015).
“We have now reached
a point where we see
not the art but the space first….
An image comes to mind
of a white, ideal space
that, more than any single picture,
may be the archetypal image
of 20th-century art.”
“Space: what you
damn well have to see.”
— James Joyce, Ulysses
The Silvia of the title is from the previous post.
For the Time Cube, see …
The assignments page for a graduate algebra course at Cornell
last fall had a link to the eightfold cube:
Nobel Flashback:
Wednesday, January 29, 2014
|
A KUNSTforum.as article online today (translation by Google) —
Update of Sept. 7, 2016: The corrections have been made,
except for the misspelling "Cullinan," which was caused by
Google translation, not by KUNSTforum.
From this journal —
See (for instance) Sacred Order, July 18, 2006 —
From a novel published July 26, 2016, and reviewed
in yesterday's (print) New York Times Book Review —
|
The doors open slowly. I step into a hangar. From the rafters high above, lights blaze down, illuminating a twelve-foot cube the color of gunmetal. My pulse rate kicks up. I can’t believe what I’m looking at. Leighton must sense my awe, because he says, “Beautiful, isn’t it?” It is exquisitely beautiful. At first, I think the hum inside the hangar is coming from the lights, but it can’t be. It’s so deep I can feel it at the base of my spine, like the ultralow-frequency vibration of a massive engine. I drift toward the box, mesmerized.
— Crouch, Blake. Dark Matter: A Novel |
See also Log24 on the publication date of Dark Matter .
Foreword by Sir Michael Atiyah —
"Poincaré said that science is no more a collection of facts
than a house is a collection of bricks. The facts have to be
ordered or structured, they have to fit a theory, a construct
(often mathematical) in the human mind. . . .
… Mathematics may be art, but to the general public it is
a black art, more akin to magic and mystery. This presents
a constant challenge to the mathematical community: to
explain how art fits into our subject and what we mean by beauty.
In attempting to bridge this divide I have always found that
architecture is the best of the arts to compare with mathematics.
The analogy between the two subjects is not hard to describe
and enables abstract ideas to be exemplified by bricks and mortar,
in the spirit of the Poincaré quotation I used earlier."
— Sir Michael Atiyah, "The Art of Mathematics"
in the AMS Notices , January 2010
Judy Bass, Los Angeles Times , March 12, 1989 —
"Like Rubik's Cube, The Eight demands to be pondered."
As does a figure from 1984, Cullinane's Cube —
For natural group actions on the Cullinane cube,
see "The Eightfold Cube" and
"A Simple Reflection Group of Order 168."
See also the recent post Cube Bricks 1984 —
Related remark from the literature —
Note that only the static structure is described by Felsner, not the
168 group actions discussed by Cullinane. For remarks on such
group actions in the literature, see "Cube Space, 1984-2003."
(From Anatomy of a Cube, Sept. 18, 2011.)
The following page quotes "Raiders of the Lost Crucible,"
a Log24 post from Halloween 2015.
From KUNSTforum.as, a Norwegian art quarterly, issue no. 1 of 2016.
Related posts — See Lyche Eightfold.
Related aesthetics —
"Poincaré said that science is no more a collection of facts
than a house is a collection of bricks. The facts have to be
ordered or structured, they have to fit a theory, a construct
(often mathematical) in the human mind. . . .
… Mathematics may be art, but to the general public it is
a black art, more akin to magic and mystery. This presents
a constant challenge to the mathematical community: to
explain how art fits into our subject and what we mean by beauty.
In attempting to bridge this divide I have always found that
architecture is the best of the arts to compare with mathematics.
The analogy between the two subjects is not hard to describe
and enables abstract ideas to be exemplified by bricks and mortar,
in the spirit of the Poincaré quotation I used earlier."
— Sir Michael Atiyah, "The Art of Mathematics"
in the AMS Notices , January 2010
Anyone who clicked on the Dirac search at the end of
the previous post, "Dirac's Diamond," may wonder why the
"Solomon's Cube" post of 11 AM Sunday, March 1, 2009,
appeared in the Dirac search results, since there is no
apparent mention of Dirac in that Sunday post.
<!– See also "a linear transformation of V6… which preserves
the Klein quadric; in this way we arrive at the isomorphism of
Sym(8) withthe full orthogonal group O+(6; 2)." in "The
Classification of Flats in PG(9,2) which are External to the
Grassmannian G1,4,2 Authors: Shaw, Ron;
 Maks, Johannes; Gordon, Neil; Source: Designs,
Codes and Cryptography, Volume 34, Numbers 2-3, February
2005 , pp. 203-227; Publisher: Springer.  For more details,
see "Finite Geometry, Dirac Groups and the Table of Real
Clifford Algebras," by R. Shaw (U. of Hull), pp. 59-99 in
Clifford Algebras and Spinor Structures, by By Albert
Crumeyrolle, Rafał Abłamowicz, Pertti Lounesto,
published by Springer, 1995. –>
An eightfold cube appears in this detail
of a photo by Josefine Lyche of her
installation "4D Ambassador" at the
Norwegian Sculpture Biennial 2015 —
(Detail from private Instagram photo.)
Catalog description of installation —
Google Translate version —
In a small bedroom to Foredragssalen populate
Josefine Lyche exhibition with a group sculptures
that are part of the work group 4D Ambassador
(2014-2015). Together they form an installation
where she uses light to amplify the feeling of
stepping into a new dimension, for which the title
suggests, this "ambassadors" for a dimension we
normally do not have access to. "Ambassadors"
physical forms presents nonphysical phenomena.
Lyches works have in recent years been placed
in something one might call an "esoteric direction"
in contemporary art, and defines itself this
sculpture group humorous as "glam-minimalist."
She has in many of his works returned to basic
geometric shapes, with hints to the occult,
"new space-age", mathematics and where
everything in between.
See also Lyche + "4D Ambassador" in this journal and
her website page with a 2012 version of that title.
For Aaron Sorkin and Walter Isaacson —
Related material —
Bauhaus Cube, Design Cube, and
Nabokov's Transparent Things .
Click to enlarge:
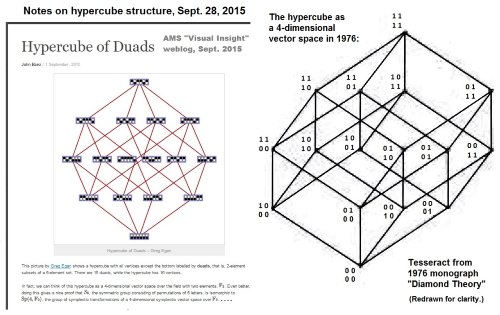
For the hypercube as a vector space over the two-element field GF(2),
see a search in this journal for Hypercube + Vector + Space .
For connections with the related symplectic geometry, see Symplectic
in this journal and Notes on Groups and Geometry, 1978-1986.
For the above 1976 hypercube (or tesseract ), see "Diamond Theory,"
by Steven H. Cullinane, Computer Graphics and Art , Vol. 2, No. 1,
Feb. 1977, pp. 5-7.
Omega is a Greek letter, Ω , used in
mathematics to denote a set on which
a group acts.
The incidences of points and planes in the
Möbius 84 configuration (8 points and 8 planes,
with 4 points on each plane and 4 planes on each point),
were described by Coxeter in a 1950 paper.*
A table from Monday's post summarizes Coxeter's
remarks, which described the incidences in
spatial terms, with the points and planes as the vertices
and face-planes of two mutually inscribed tetrahedra —
Monday's post, "Gallucci's Möbius Configuration,"
may not be completely intelligible unless one notices
that Coxeter has drawn some of the intersections in his
Fig. 24, a schematic representation of the point-plane
incidences, as dotless, and some as hollow dots. The figure,
"Gallucci's version of Möbius's 84," is shown below.
The hollow dots, representing the 8 points (as opposed
to the 8 planes ) of the configuration, are highlighted in blue.
Here a plane (represented by a dotless intersection) contains
the four points that are represented in the square array as lying
in the same row or same column as the plane.
The above Möbius incidences appear also much earlier in
Coxeter's paper, in figures 6 and 5, where they are shown
as describing the structure of a hypercube.
In figures 6 and 5, the dotless intersections representing
planes have been replaced by solid dots. The hollow dots
have again been highlighted in blue.
Figures 6 and 5 demonstrate the fact that adjacency in the set of
16 vertices of a hypercube is isomorphic to adjacency in the set
of 16 subsquares of a square 4×4 array, provided that opposite
sides of the array are identified, as in Fig. 6. The digits in
Coxeter's labels above may be viewed as naming the positions
of the 1's in (0,1) vectors (x4, x3, x2, x1) over the two-element
Galois field.† In that context, the 4×4 array may be called, instead
of a Möbius hypercube , a Galois tesseract .
* "Self-Dual Configurations and Regular Graphs,"
Bulletin of the American Mathematical Society,
Vol. 56 (1950), pp. 413-455
† The subscripts' usual 1-2-3-4 order is reversed as a reminder
that such a vector may be viewed as labeling a binary number
from 0 through 15, or alternately as labeling a polynomial in
the 16-element Galois field GF(24). See the Log24 post
Vector Addition in a Finite Field (Jan. 5, 2013).
The Blacklist “Pilot” Review
"There is an element of camp to this series though. Spader is
quite gleefully channeling Anthony Hopkins, complete with being
a well educated, elegant man locked away in a super-cell.
Speaking of that super-cell, it’s kind of ridiculous. They’ve got him
locked up in an abandoned post office warehouse on a little
platform with a chair inside a giant metal cube that looks like
it could have been built by Tony Stark. And as Liz approaches
to talk to him, the entire front of the cube opens and the whole
thing slides back to leave just the platform and chair. Really?
FUCKING REALLY ? "
— Kate Reilly at Geekenstein.com (Sept. 27, 2013)
Continued from Nobel Note (Jan. 29, 2014).
From Tradition in Action , "The Missal Crisis of '62,"
remarks on the revision of the Catholic missal in that year—
"Neither can the claim that none of these changes
is heretical in content be used as an argument
in favor of its use, for neither is the employment of
hula girls, fireworks, and mariachis strictly speaking
heretical in itself, but they belong to that class of novel
and profane things that do not belong in the Mass."
— Fr. Patrick Perez, posted Sept. 11, 2007
See also this journal on November 22, 2014…
… and on Bruce Springsteen's birthday this year —
Tuesday, September 23, 2014
|
A sequel to this afternoon’s Rubik Quote:
“The Cube was born in 1974 as a teaching tool
to help me and my students better understand
space and 3D. The Cube challenged us to find
order in chaos.”
— Professor Ernő Rubik at Chrome Cube Lab
(Click image below to enlarge.)
The archived Java rotatable hypercube of
Harry J. Smith is no longer working.
For an excellent JavaScript replacement,
see Pete Michaud's
http://petemichaud.github.io/4dhypercube/.
This JavaScript version can easily be saved.
From Night of Lunacy (Sunday, May 5, 2013):
Related posts: Rubric, Cuber, and Pound Sign.
Click image for some background.
See also Story Theory and Princeton Apocalypse.
For the late Cardinal Glemp of Poland,
who died yesterday, some links:
|
From Don DeLillo's novel Point Omega — I knew what he was, or what he was supposed to be, a defense intellectual, without the usual credentials, and when I used the term it made him tense his jaw with a proud longing for the early weeks and months, before he began to understand that he was occupying an empty seat. "There were times when no map existed to match the reality we were trying to create." "What reality?" "This is something we do with every eyeblink. Human perception is a saga of created reality. But we were devising entities beyond the agreed-upon limits of recognition or interpretation. Lying is necessary. The state has to lie. There is no lie in war or in preparation for war that can't be defended. We went beyond this. We tried to create new realities overnight, careful sets of words that resemble advertising slogans in memorability and repeatability. These were words that would yield pictures eventually and then become three-dimensional. The reality stands, it walks, it squats. Except when it doesn't." He didn't smoke but his voice had a sandlike texture, maybe just raspy with age, sometimes slipping inward, becoming nearly inaudible. We sat for some time. He was slouched in the middle of the sofa, looking off toward some point in a high corner of the room. He had scotch and water in a coffee mug secured to his midsection. Finally he said, "Haiku." I nodded thoughtfully, idiotically, a slow series of gestures meant to indicate that I understood completely. "Haiku means nothing beyond what it is. A pond in summer, a leaf in the wind. It's human consciousness located in nature. It's the answer to everything in a set number of lines, a prescribed syllable count. I wanted a haiku war," he said. "I wanted a war in three lines. This was not a matter of force levels or logistics. What I wanted was a set of ideas linked to transient things. This is the soul of haiku. Bare everything to plain sight. See what's there. Things in war are transient. See what's there and then be prepared to watch it disappear." |
What's there—
This view of a die's faces 3, 6, and 5, in counter-
clockwise order (see previous post) suggests a way
of labeling the eight corners of a die (or cube):
123, 135, 142, 154, 246, 263, 365, 456.
Here opposite faces of the die sum to 7, and the
three faces meeting at each corner are listed
in counter-clockwise order. (This corresponds
to a labeling of one of MacMahon's* 30 colored cubes.)
A similar vertex-labeling may be used in describing
the automorphisms of the order-8 quaternion group.
For a more literary approach to quaternions, see
Pynchon's novel Against the Day .
* From Peter J. Cameron's weblog:
"The big name associated with this is Major MacMahon,
an associate of Hardy, Littlewood and Ramanujan,
of whom Robert Kanigel said,
His expertise lay in combinatorics, a sort of
glorified dice-throwing, and in it he had made
contributions original enough to be named
a Fellow of the Royal Society.
Glorified dice-throwing, indeed…"
Continued from April 2, 2012.
Some predecessors of the Cullinane design cubes of 1984
that lack the Cullinane cubes' symmetry properties—
Kohs cubes (see 1920 article)
Wechsler cubes (see Wechsler in this journal), and
Horowitz cubes (see links below).
Last Wednesday's 11 PM post mentioned the
adjacency-isomorphism relating the 4-dimensional
hypercube over the 2-element Galois field GF(2) to
the 4×4 array made up of 16 square cells, with
opposite edges of the 4×4 array identified.
A web page illustrates this property with diagrams that
enjoy the Karnaugh property— adjacent vertices, or cells,
differ in exactly one coordinate. A brief paper by two German
authors relates the Karnaugh property to the construction
of a magic square like that of Dürer (see last Wednesday).
In a similar way (search the Web for Karnaugh + cube ),
vertex adjacency in the 6-dimensional hypercube over GF(2)
is isomorphic to cell adjacency in the 4x4x4 cube, with
opposite faces of the 4x4x4 cube identified.
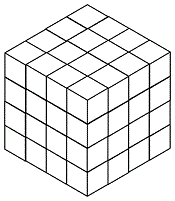
The above cube may be used to illustrate some properties
of the 64-point Galois 6-space that are more advanced
than those studied by enthusiasts of "magic" squares
and cubes.
See
Those who prefer narrative to mathematics may
consult posts in this journal containing the word "Cuber."
Denote the d-dimensional hypercube by
"… after coloring the sixty-four vertices of
alternately red and blue, we can say that
the sixteen pairs of opposite red vertices represent
the sixteen nodes of Kummer's surface, while
the sixteen pairs of opposite blue vertices
represent the sixteen tropes."
— From "Kummer's 166 ," section 12 of Coxeter's 1950
"Self-dual Configurations and Regular Graphs"
Just as the 4×4 square represents the 4-dimensional
hypercube
so the 4x4x4 cube represents the 6-dimensional
hypercube
For religious interpretations, see
Nanavira Thera (Indian) and
I Ching geometry (Chinese).
See also two professors in The New York Times
discussing images of the sacred in an op-ed piece
dated Sept. 26 (Yom Kippur).
The second Logos figure in the previous post
summarized affine group actions on partitions
that generate a group of about 1.3 trillion
permutations of a 4x4x4 cube (shown below)—
Click for further details.
For Pete Rustan, space recon expert, who died on June 28—
See also Galois vs. Rubik and Group Theory Template.
Yesterday's post Child's Play displayed a cube formed
by a Hasse diagram of the 8 subsets of a 3-set.*
This suggests a review of a post from last January—
* See a comment on yesterday's post relating it to earlier,
very similar, remarks by Margaret Masterman.
I was unaware yesterday that those remarks exist.
See also Finite Geometry and Physical Space.
Related material from MacTutor—
The paper by J. W. Shirley, Binary numeration before Leibniz, Amer. J. Physics 19 (8) (1951), 452-454, contains an interesting look at some mathematics which appears in the hand written papers of Thomas Harriot [1560-1621]. Using the photographs of the two original Harriot manuscript pages reproduced in Shirley’s paper, we explain how Harriot was doing arithmetic with binary numbers. Leibniz [1646-1716] is credited with the invention [1679-1703] of binary arithmetic, that is arithmetic using base 2. Laplace wrote:-
However, Leibniz was certainly not the first person to think of doing arithmetic using numbers to base 2. Many years earlier Harriot had experimented with the idea of different number bases…. |
For a discussion of Harriot on the discrete-vs.-continuous question,
see Katherine Neal, From Discrete to Continuous: The Broadening
of Number Concepts in Early Modern England (Springer, 2002),
pages 69-71.
A search today (Élie Cartan's birthday) for material related to triality*
yielded references to something that has been called a Bhargava cube .
Two pages from a 2006 paper by Bhargava—
Bhargava's reference [4] above for "the story of the cube" is to…
Higher Composition Laws I:
A New View on Gauss Composition,
and Quadratic Generalizations
Manjul Bhargava
The Annals of Mathematics
Second Series, Vol. 159, No. 1 (Jan., 2004), pp. 217-250
Published by: Annals of Mathematics
Article Stable URL: http://www.jstor.org/stable/3597249
A brief account in the context of embedding problems (click to enlarge)—
For more ways of slicing a cube,
see The Eightfold Cube —
* Note (1) some remarks by Tony Smith
related to the above Dynkin diagram
and (2) another colorful variation on the diagram.
Click images for further details.
See also Crimson Tide, Rubik, and Cuber.
For another monochromatic enigma without
guaranteed equality of results, see
Finite Geometry of the Square and Cube.
“Examples galore of this feeling must have arisen in the minds of the people who extended the Magic Cube concept to other polyhedra, other dimensions, other ways of slicing. And once you have made or acquired a new ‘cube’… you will want to know how to export a known algorithm , broken up into its fundamental operators , from a familiar cube. What is the essence of each operator? One senses a deep invariant lying somehow ‘down underneath’ it all, something that one can’t quite verbalize but that one recognizes so clearly and unmistakably in each new example, even though that example might violate some feature one had thought necessary up to that very moment. In fact, sometimes that violation is what makes you sure you’re seeing the same thing , because it reveals slippabilities you hadn’t sensed up till that time….
… example: There is clearly only one sensible 4 × 4 × 4 Magic Cube. It is the answer; it simply has the right spirit .”
— Douglas R. Hofstadter, 1985, Metamagical Themas: Questing for the Essence of Mind and Pattern (Kindle edition, locations 11557-11572)
See also Many Dimensions in this journal and Solomon’s Cube.
The following picture provides a new visual approach to
the order-8 quaternion group's automorphisms.
Click the above image for some context.
Here the cube is called "eightfold" because the eight vertices,
like the eight subcubes of a 2×2×2 cube,* are thought of as
independently movable. See The Eightfold Cube.
See also…
Related material: Robin Chapman and Karen E. Smith
on the quaternion group's automorphisms.
* See Margaret Wertheim's Christmas Eve remarks on mathematics
and the following eightfold cube from an institute she co-founded—
Photo by Norman Brosterman
fom the Inventing Kindergarten
exhibit at The Institute for Figuring
(co-founded by Margaret Wertheim)
The hypercube has 192 rotational symmetries.
Its full symmetry group, including reflections,
is of order 384.
See (for instance) Coxeter—
Related material—
The rotational symmetry groups of the Platonic solids
(from April 25, 2011)—
— and the figure in yesterday evening's post on the hypercube—
(Animation source: MIQEL.com)
Clearly hypercube rotations of this sort carry any
of the eight 3D subcubes to the central subcube
of a central projection of the hypercube—
The 24 rotational symmeties of that subcube induce
24 rigid rotations of the entire hypercube. Hence,
as in the logic of the Platonic symmetry groups
illustrated above, the hypercube has
rotational symmetries.
R.D. Carmichael’s seminal 1931 paper on tactical configurations suggests
a search for later material relating such configurations to block designs.
Such a search yields the following—
“… it seems that the relationship between
BIB [balanced incomplete block ] designs
and tactical configurations, and in particular,
the Steiner system, has been overlooked.”
— D. A. Sprott, U. of Toronto, 1955
The figure by Cullinane included above shows a way to visualize Sprott’s remarks.
For the group actions described by Cullinane, see “The Eightfold Cube” and
“A Simple Reflection Group of Order 168.”
Update of 7:42 PM Sept. 18, 2011—
From a Summer 2011 course on discrete structures at a Berlin website—
A different illustration of the eightfold cube as the Steiner system S(3, 4, 8)—
Note that only the static structure is described by Felsner, not the
168 group actions discussed (as above) by Cullinane. For remarks on
such group actions in the literature, see “Cube Space, 1984-2003.”
Prequel — (Click to enlarge)
Background —
See also Rubik in this journal.
* For the title, see Groups Acting.
The New York Times has a skateboarder obit with a URL date of July 9.
Here is an earlier version from the LA Times—
By Keith Thursby, Los Angeles Times
Chris Cahill, one of the original Dogtown Z-Boys
who brought seismic changes to skateboarding
with their style and attitude, has died. He was 54.
Cahill was found June 24 at his Los Angeles home,
said Larry Dietz of the Los Angeles County
coroner's office. A cause of death has not been
determined and tests are ongoing, Dietz said.
Related material from Midsummer Day, June 24, the day Cahill was found dead—
The Gleaming and The Cube.
An illustration from the latter—
The above was adapted from a 1996 cover—
Vintage Books, July 1996. Cover: Evan Gaffney.
For the significance of the flames,
see PyrE in the book. For the significance
of the cube in the altered cover, see
The 2×2×2 Cube and The Diamond Archetype.
The 3×3×3 Galois Cube
This cube, unlike Rubik's, is a
purely mathematical structure.
Its properties may be compared
with those of the order-2 Galois
cube (of eight subcubes, or
elements ) and the order-4 Galois
cube (of 64 elements). The
order-3 cube (of 27 elements)
lacks, because it is based on
an odd prime, the remarkable
symmetry properties of its smaller
and larger cube neighbors.
Click the above image for some background.
Related material:
Skateboard legend Andy Kessler,
this morning's The Gleaming,
and But Sometimes I Hit London.
The title refers not to numbers of the form p 3, p prime, but to geometric cubes with p 3 subcubes.
Such cubes are natural models for the finite vector spaces acted upon by general linear groups viewed as permutation groups of degree (not order ) p 3.
For the case p =2, see The Eightfold Cube.
For the case p =3, see the "External links" section of the Nov. 30, 2009, version of Wikipedia article "General Linear Group." (That is the version just prior to the Dec. 14, 2009, revision by anonymous user "Greenfernglade.")
For symmetries of group actions for larger primes, see the related 1985 remark* on two -dimensional linear groups—
"Actions of GL(2,p ) on a p ×p coordinate-array
have the same sorts of symmetries,
where p is any odd prime."
It was a dark and stormy night…
— Page 180, Logicomix
“… the class of reflections is larger in some sense over an arbitrary field than over a characteristic zero field.”
– Julia Hartmann and Anne V. Shepler, “Jacobians of Reflection Groups”
For some context, see the small cube in “A Simple Reflection Group of Order 168.”
See also the larger cube in “Many Dimensions” + Whitehead in this journal (scroll down to get past the current post).
That search refers to a work by Whitehead published in 1906, the year at the top of the Logicomix page above—
A related remark on axiomatics that has metaphysical overtones suitable for a dark and stormy night—
“An adequate understanding of mathematical identity requires a missing theory that will account for the relationships between formal systems that describe the same items. At present, such relationships can at best be heuristically described in terms that invoke some notion of an ‘intelligent user standing outside the system.'”
— Gian-Carlo Rota, “Syntax, Semantics, and…” in Indiscrete Thoughts . See also the original 1988 article.
Cubic models of finite geometries
display an interplay between
Euclidean and Galois geometry.
Example 1— The 2×2×2 Cube—
also known as the eightfold cube—
Group actions on the eightfold cube, 1984—
Version by Laszlo Lovasz et al., 2003—
Lovasz et al. go on to describe the same group actions
as in the 1984 note, without attribution.
Example 2— The 3×3×3 Cube
A note from 1985 describing group actions on a 3×3 plane array—
Undated software by Ed Pegg Jr. displays
group actions on a 3×3×3 cube that extend the
3×3 group actions from 1985 described above—
Pegg gives no reference to the 1985 work on group actions.
Example 3— The 4×4×4 Cube
A note from 27 years ago today—
As far as I know, this version of the
group-actions theorem has not yet been ripped off.
A search for “Chinese Cube” (based on the the previous entry’s title) reveals the existence of a most interesting character, who…
“… has attempted in his books to produce a Science and Art of Reasoning using the simplest of the Platonic solids, the Cube. [His] model also parallels, in some ways, the Cube of Space constructed from the Sepher Yetzirah’s attributions for the Hebrew letters and their direction. [He] elucidated his theories at great length….”
— More…
For related remarks, see the link to Solomon’s Cube from the previous entry.
Then of course there is…
Click on figure for details.
From the Bulletin of the American Mathematical Society, Jan. 26, 2005:
What is known about unit cubes
by Chuanming Zong, Peking University
Abstract: Unit cubes, from any point of view, are among the simplest and the most important objects in n-dimensional Euclidean space. In fact, as one will see from this survey, they are not simple at all….
From Log24, now:
What is known about the 4×4×4 cube
by Steven H. Cullinane, unaffiliated
Abstract: The 4×4×4 cube, from one point of view, is among the simplest and the most important objects in n-dimensional binary space. In fact, as one will see from the links below, it is not simple at all.
The Klein Correspondence, Penrose Space-Time, and a Finite Model
Related material:
Monday's entry Just Say NO and a poem by Stevens,
|
"Chang noted that 'the story starts slowly, for
1. Chang, Margaret A. "The King in the Window". |
Some will prefer exposition more closely related to Chicago.
From a Log24 search for that word . . .
The above phrase "the intersection of storytelling and visual arts"
suggests a review . . .
Some exposition that does not go back thousands of years —
Addendum for Christopher Nolan — Dice and the Eightfold Cube.
One of a Kind Malfunction
|
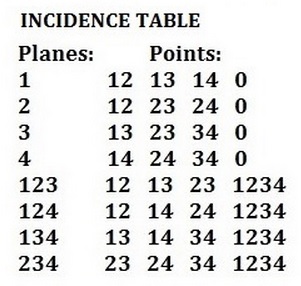
Cullinane Diamond Theorem Research Report by https://you.com/?chatMode=research on March 3, 2024 Overview of the Cullinane Diamond Theorem The Cullinane Diamond Theorem is a mathematical concept developed by Steven H. Cullinane that explores the symmetrical properties of certain geometric patterns. It is particularly concerned with the structure of finite projective geometry as it relates to the 35 square patterns found in R. T. Curtis's Miracle Octad Generator (MOG). The theorem asserts that every G-image of a diamond figure D possesses some form of ordinary or color-interchange symmetry. Symmetry and Group Theory The theorem is deeply rooted in group theory, with G being isomorphic to the affine group A on the linear 4-space over the finite field GF(2). This group has a significant order of 322,560 and underlies the symmetry of both the diamond-theorem figures and the square patterns of the MOG . The 35 structures of the 840 G-images of D are isomorphic to the 35 lines in the 3-dimensional projective space over GF(2), which explains the symmetry of the line diagrams and the two-color patterns. The Diamond Theorem in Various Dimensions The diamond theorem can be applied to different cases, such as the 4×4, 2×2, and even 3-dimensional cubes like the 2x2x2 and 4x4x4 cubes. The generalized statement of the theorem involves inscribing a white diamond in a black square and dividing it into four quadrants, each with a diagonal split into black and white halves. Algebraic Implications The theorem has algebraic implications, such as the ability to express every 4-coloring as a sum of three 2-colorings. This algebraic formulation is useful for demonstrating that certain four-colored graphic images can form a ring under multiplication. There is also an infinite family of such 'diamond' rings, isomorphic to rings of matrices over GF(4). Philosophical and Cultural Context Steven H. Cullinane has also explored the philosophical implications of the diamond theorem, referring to it in the context of Plato's Meno dialogue and opposing it to the 'Story Theory of truth' as discussed by Richard J. Trudeau. The theorem is seen as a correct statement of the relation between geometry and the physical universe. Clarification on Cullinan Diamonds It is important to note that the Cullinane Diamond Theorem is unrelated to the Cullinan diamond, which is a famous large gemstone discovered in South Africa and now part of the British Crown Jewels. The Cullinan diamond has its own historical and cultural significance, with its various cut shapes and ownership history. In summary, the Cullinane Diamond Theorem is a mathematical concept that reveals the symmetrical properties of certain geometric patterns, with applications in group theory and algebra. It also has philosophical implications, drawing connections to classical ideas about truth and geometry. |
Instagram ad for You.com AI in research mode
"Show me ALL your sources, babe."
— Line adapted from Leonardo DiCaprio
In memory of the inventor of the Pascal programming language,
who reportedly died on New Year's Day, 2024, an image from
this journal on that date —
"Before time began, there was the Cube." — Optimus Prime
See as well a Pascal that some will prefer, and my own ACM card.
That card gives Warren, PA, as my location… which is no longer
always the case… but Warren is where I learned, and worked, in
computing, after a somewhat belated education in pure mathematics
in New York State.
Some personal background is suggested by…
The epigraph of the previous post —
"To Phaedrus, this backlight from the conflict between
the Sophists and the Cosmologists adds an entirely
new dimension to the Dialogues of Plato." — Robert M. Pirsig
Related reading and art for academic nihilists — See . . .
Reading and art I prefer —
Love in the Ruins , by Walker Percy, and . . .
Van Gogh (by Ed Arno) and an image and
a passage from The Paradise of Childhood
(by Edward Wiebé):
Powered by WordPress
